,= 2..... ,3.4.2,

дХ; дх, дх,

1=2

дифференцирование же по а дает

Е

,= 2.....n-l. (3.4.3,

дх. да да

Положим в равенствах (3.4.2) и (3.4.3) х = х* и а = а*. Мы получим две системы линейных алгебраических уравнений

С d<f афА

для нахождения искомых величин и -1 имеющие одну

и ту же матрицу коэффициентов Ji. По предположению (см. (3.3.8)) матрица Ji невырожденна и, следовательно, эти системы однозначно разрешимы.

3.4.2. Устойчивость на диаграмме стационарных решений

На диаграмме стационарных решений обычно указывается и характер устойчивости этих решений, при этом сплошной линией мы изображаем ветви устойчивых стационарных решений, а пунктирной линией ветви неустойчивых стационарных решений. Изменение характера устойчивости происходит обыкновенно в точках поворота и в точках ветвления. Изменение характера устойчивости может произойти и в обыкновенной (регулярной) точке диаграммы стационарных решений, например

6 М. Холодниок н др.

3.4. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ

3.4.1. Нахождение касательных векторов

Пусть в критической точке (х*,а*) множества S(f) пересекаются две дуги этого множества (рис. 3.3а). Наша цель (это потребуется нам в гл. 5) состоит в том, чтобы найти в этой точке касательные векторы к обеим дугам, т. е. определить величины (dxi/da) {а*), i= 1,2, п.

Дифференцируя формулу (3.3.9) по а, получаем

= Sf + %. .....(3.4.1,

Значения производных (d(pjdxj (л;, а'), (5ф^/5а) [х', а'), i = 2, п можно определить следующим образом. Дифференцируя тождества (3.3.10) по Хи находим

Рис. 3.4. Диаграмма стационарных решений.

В точке, отвечающей бифуркации Андронова-Хопфа. При этом на диаграмме стационарных решений мы символически обозначаем малыми кружками отделившиеся периодические решения (рис. 3.4). Черными кружками обозначаются устойчивые периодические решения, а белыми (незаштрихованными) кружками - неустойчивые.

3.4.3. Диаграмма периодических решений

Диаграмма периодических решений строится аналогично диаграмме стационарных решений: на двумерной картинке отображается зависимость той или иной характеристики периодического решения от параметра. Обычно в качестве такой характеристики мы выбираем период или амплитуду периодического решения. Устойчивые и неустойчивые периодические решения на этих диаграммах мы обозначаем соответственно сплошными-и пунктирными линиями.

Изменение характера устойчивости происходит обычно в точках поворота и в точках, где пересекаются две дуги диаграммы. Точки поворота иа диаграмме периодических решений соответствуют бифуркациям, при которых с изменением параметра происходит слияние и исчезновение (или соответственно возникновение) пары периодических решений. Точке пересечения двух дзт соответствует обыкновенно бифуркация периодического решения с потерей симметрии. Изменение характера устойчивости происходит и в обыкновенных (регулярных) точках диаграммы периодических решений, а именно в точках, соответствующих бифуркации удвоения периода или бифзфкации рождения нива-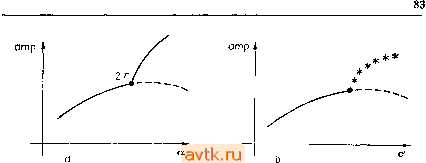

Рнс. 3.5. Диаграмма периодических решений: а) удвоение периода; Ь) рождение инвариантного тора.

риантного тора. Ветвь периодических решений с двойным периодом на диаграмме периодических решений обозначается способом, указанным на рис. 3.5а. Ответвление семейства инвариантных торов изображено графически на рис. 3.5й.

ЛИТЕРАТУРА

13.1] looss G., Joseph D. D.: Elementary Stability and Bifurcation Theory, Springer -Verlag, New York, 1980. [Имеется перевод: Йосс Ж., Джозеф Д. Элементарная теория устойчивости и бифуркаций. - М.: Мир, 1983.]

13.2] Kubicek М., КИс А.: Appl. Math, and Comput. 13 (1983), 125.

Глава 4

МАТЕМАТИЧЕСКИЕ МОДЕЛИ

в начале этой главы (в § 4.1) мы коротко обсудим построение математических моделей. На примере неизотермическога проточного реактора мы рассмотрим некоторые методы анализа моделей, включая приведение уравнений к безразмерному виду.

Следующие параграфы содержат набор моделей для систем с сосредоточенными параметрами (§ 4.2) и с распределенными параметрами (§ 4.3). В последующих главах эти модели будут служить для иллюстрации различных численных методов и подходов,

4.1. ПОСТРОЕНИЕ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ

4.1.1. Соотношения баланса

Выделим некоторый элемент объема и запишем соотношение баланса для какой-нибудь физической величины (например для массы одного из компонентов в смеси веществ). Пусть скорость поступления рассматриваемой величины в выделенный элемент объема есть Р, скорость ее возникновения R, а ее общее количество в данном объеме М. Тогда Р, R и М являются функциями времени, связанными между собой соотношениями

P-fR = dM/d/. (4.1.1>

В случае сплошной среды величины Р, R и М мы должны определить через некоторые плотности. Вектором р обозначим плотность потока, определенную таким образом, что поток через: элемент с поверхностью dS в направлении нормали к ней п равен p-ndS. Аналогичным образом скорость возникновения величины г рассчитывается на единицу объема, так что в элементе объема dV скорость возникновения оказывается равной

r-dV. Наконец, величина М описывается концентрацией т. Пусть теперь Q - произвольная область сплошной среды с кусочно-гладкой поверхностью dQ (внешнюю нормаль к этой поверхности обозначим через п). Тогда имеет место соотношение

+ = (4.1.2)

дИ Р- Q

Используя формулу Грина и перенося все члены равенства (4.1.2) в одну сторону (область Q фиксирована, и поэтому можно поменять порядок интегрирования и дифференцирования), мы получаем

[[\[ + divp-r]dV =0. (4.1.3)

В силу произвольности области Q должно выполняться соотношение

-divp + r = . (4.1.4)

Уравнения балансов могут быть также записаны для движущегося элемента объема (см. [4.8], [4.9]).

4.1.2. Модель реактора проточного типа с перемешиванием

В качестве примера построим математическую модель химического реактора проточного типа с перемешиванием. Рассмотрим цилиндрический сосуд объемом V, снабженный охлаждающим кожухом объемом Vc (см. рис. 4.1а). В реактор подаются в виде растворов компоненты реакционной смеси АьАг, .4. с объемными притоками Fk, а из реактора отводятся

продукты реакции А^+ь A+g, As вместе с непрореагировав-шими компонентами реакционной смеси, имеющие суммарный объёмный расход на выходе F (очевидно, что = Fi 4- -2 + ... -{-Fk). В реакторе происходит химическая реакция, описываемая стехиометрическим соотношением

EvЛ^ = 0, (4.1.5)

где стехиометрические коэффициенты веществ, вступающих в реакцию vi, ..., v, отрицательны, а стехиометрические коэффициенты продуктов реакции v+i, положительны. В полностью перемешиваемый объем охлаждающей среды Vc

поступает хладагент с объемным расходом Fc и с температурой Гсо. Будем предполагать, что выполнены следующие условия: - перемешивание реакционной смесн и охлаждающей среды является полным, в результате чего молярные концентрации реагирующих компонент с/, температура реагирующей смеси и температура охлаждающей среды Т не зависят от координат и могут быть только функциями времени;

fJadava

г

О' So

Подача J ,1 i Отвод j(/!ada2EHma \ х/гаЗагента

Fc.Tc ,::~~-::ХлаЗагет

Отвод продуктов

F с Т Од/юсть W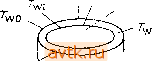

RoSspxHomb

Поверхность So

Рис. 4.1. a) Реактор проточного типа с перемешиванием, б) Температуры в резервуаре.

- объемы V и Ус, притоки Fj, расход на выходе F, расход Fc, температура реакционной смеси на входе Го и охлаждающей смеси на входе Гсо являются постоянными;

- работа, совершаемая при перемешивании реакционной смеси и охлаждающей среды, с точки зрения баланса энергии пренебрежимо мала;

- скорость реакции представляет собой такую функцию r(ci, Cs,T), что изменение числа молей компоненты ре-.акции А/ на единицу объема равно v,r;

- удельная теплоемкость реакционной смеси Ср (на единицу объема) постоянна.

Обозначим температуру внутренней стенки реактора через Twi, а температуру внешней стенки - через Two] предположим далее, что в соответствии с законом охлаждения Ньютона тепловой поток на единицу поверхности задается выражениями вида ai{T - 7wi)h ао(Го - Тс), где ао и а, - коэффициенты теплоотдачи на внешней и внутренней поверхностях теплообменной стенки (при этом мы считаем их постоянными).

Используя общее уравнение баланса (4.1.1), где

P = FiC,o - Fcj, R = v/yr и IA = Vc,;

находим

--F,c,-Fc, + v,Vr{c с„ Т). (4.1.6)

Если обозначить через h,[T) молярную энтальпию компоненты А, и пренебречь работой, совершаемой при перемешивании, то, применяя аналогичным образом закон сохранения энергии (см. [4.8], [4.5]), получаем

ж Е А = Z Ао -pY.- г-т^ (4.1.7)

Здесь /г,о обозначает энтальпию компоненты на входе в реактор, Sl представляет собой суммарную внутреннюю поверхность теплообмена и Г,- среднюю температуру внутренней поверхности стенки.

Преобразуем теперь уравнение (4.1.7), вычтя из него сумму уравнений, получаемых из (4.1.6) путем умножения на соответствующую величину h, В результате мы получим соотношение вида

1.1ЧГ-Т. (ft/0 - h,) - v;ft;) Vr - S,a, {T - f,)

(4.1.8)

Здесь X v/ft/= теплота реакции.

Далее можно записать

р dt

где Ср, - молярная теплоемкость компоненты А а Ср - теплоемкость реакционной смеси на единицу объема. Считая Ср постоянным и положив

ZF,c,o{hio-h,) = FC,(To~T),

мы в конечном счете получим

= FC (Го - Г) + {-АНг) Vr (с,-----с,Т) - S,a, (Г - Г.).

(4.1.9>

(4.1.11)

Запишем теперь уравнения баланса для процесса теплопередачи через стенку. Предположим, что стенка имеет форму полого цилиндра и что она занимает область W с внутренней и внешней поверхностями Si и So соответственно (рис. 4.lb). Для температуры материала стенки Т^/ можно написать уравнение

PwCpw -jf- = wVTw, (4.1.10)

где pw, Cpw, W - соответственно плотность, удельная теплоемкость (на единицу объема) и коэффициент теплопроводности етенки. Граничные условия для уравнения (4.1.10) можно записать в виде

=00(70-Two) на So, (4.1.12)

где (9/(9п - производная в направлении нормали к Si или Sq.

Уравнение баланса энергии для охлаждающей среды имеет вид

V,C,c = F,C,c {Too - То) + Soao (Г^го - Т,). (4.1.13)

Здесь Срс - теплоемкость охлаждающей жидкости на единицу объема, а Two - средняя температура наружной стенки реактора.

Уравнения (4.1.6), (4.1.9), (4.1.10), (4.1.13) с граничными условиями (4.1.11), (4.1.12) и соответствующими начальными условиями образуют систему из s -j-2 обыкновенных дифференциальных уравнений и одного дифференциального уравнения е частными производными.

Описанная модель сравнительно сложна по своей структуре. Ее можно упростить, вводя различного рода упрощающие предположения.

4.1.2.1. Упрощенная модель стационарного режима

Прежде всего предположим, что система находится в стационарном состоянии. Тогда мы получаем уравнение Лапласа для температуры Tw вместе с системой алгебраических урав-иений.

Из уравнения Лапласа нетрудно вывести следующее соотношение, означающее равенство потоков тепла:

SiOi [Т - Тт) = Sooo (fwo - Г,), (4.1.14)

Если толщина стенки равна cfw, а диаметр реактсра гораздо больше, чем cfw, то приближенно So = Si = S и Qc = (Twi- - rwo)/rfw, откуда

Стационарное состояние реактора описывается теперь уравнением баланса массы (4.1.17) (см. (4.1.6)) и уравнением баланса энтальпии (вытекающим из уравнений (4.1.9) и (4.1.16)).

F,c,a-Fc, + viVr{cu с„ Г) = 0, /=1, .... s, (4.1.17)

FC {То -Т) + {- АЯ.) Vr (Си с„ T)-US{T- Г,о) = 0.

(4.1.18)

4.1.2.2. Упрощенные модели нестационарного режима

Будем считать теперь, что температура стенки Tw во всех ее точках приблизительно одинакова и зависит только от времени. Тогда вместо уравнения теплопроводности (4.1.10) можно записать обыкновенное дифференциальное уравнение, имеющее ясный физический смысл (уравнение баланса тепла); его можно получить также предельным переходом Я\у-> э из (4.1.10):

1wPwCpw = a,S, (Г - Tw) + OoSo (Г, - Tw). (4.1.19)

Таким образом, мы получили модель нестационарного режима работы реактора, представляющую собой систему s -f 3 обыкновенных дифференциальных уравнений (4.1.6), (4.1.9), (4.1.13) и (4.1.19).

Другую модель мы получим, если W имеет конечное значение, а теплоемкость стенки реактора пренебрежимо мала. Если предположить к тому же, что толщина стенки гораздо меньше,.

где величины, отмеченные черточками, представляют собой соответствующие средние температуры. Комбинируя (4.1.14) и (4.1.13), получим соотношение для скорости отвода тепла Qc в виде

Qo = F,Cp, (Г, - Г,о) = Sodo (Two - Т,) = S,c- (Г - Тш). (4.1.15) Отсюда находим

чем диаметр реактора, то из условия равенства тепловых потоков получим

Qc = 5ао (Two - Тс) = SX\v (Т\щ - Tm)/dw =

= Soi (Г - fwO = SU, (Г - П). (4.1.20)

Здесь Ui - суммарный коэффициент переноса тепла:

В этом случае мы получаем модель нестационарного режима работы реактора, состоящую из s + 2 обыкновенных дифференциальных уравнений, т. е. s уравнений вида (4.1.6), а также уравнений

VC = FC (Го - Г) + (- АЯг) Vr (Си ..., с„ Г) - SU, (Г - Г,),

(4.1.21)

VcCpc = FcCpa (Too - Тс) + SU,(T- Тс). (4.1.22)

Из анализа выщеприведенных моделей видно, что характер модели и размерность задачи в значительной степени определяются выбранными предположениями.

4.1.2.3. Приведение модели к безразмерному виду

Существенным щагом в процессе преобразования модели является приведение ее к безразмерному виду. При этом часто достигается уменьщение числа параметров.

Проиллюстрируем этот подход на примере алгебраических уравнений (4.1.17), (4.1.18), описывающих упрощенную модель стационарного режима работы реактора. Предположим, что есть одна необратимая реакция п-то порядка типа А->продукты реакции с соотношением для скорости реакции вида г =

= k- Са. Здесь константа скорости реакции k задается в форме Аррениуса, т. е.

(Г) = (Го)ехр{-(-)}.

Мы получаем следующие два алгебраических уравнения для сд и Г (учтя, что Fa = F)

FcKo-FcK-k-cl-V = 0, (4.1.23)

FC (Го - г) + (- АЯг) Vkcl -US(T-Tco)=0. (4.1.24)