График функции л;1 = ф() имеет вид, изображенный на рис. 2.43. Положив и = ф(2 - ct), мы получаем бегущую волну типа фронтам, перемещающуюся вдоль оси z со скоростью с'>.

ЛИТЕРАТУРА

[2.1] Nagy J.: Soustavy obycejnych differencialnich rovnic, SNTL, Praha, 1980.

[2.2] Степанов В. В. Курс дифференциальных уравнений. - М.: Гостехиздат, 1953. -468 с.

[2.3] Матвеев Н. М. Дифференциальные уравнения. - Минск: Высшая школа, 1968.

[2.4] Понтрягнн Л. С. Обыкновенные дифференциальные уравнения. - М.: Наука, 1974.

2.5] Kurzweil J.: Obycejne differencialnl rovnice, SNTL, Praha, 1978. 2.61 Hartman P.: Ordinary Differential Equations. J. Wiley, New York, 1964. .2.7] Coddington E. A., Levinson N.: Theory of Ordinary Differential Equations, McGraw-Hill, New York, 1955. Имеется перевод: Коддннгтон Э., Левннсон Н. Теория обыкновенных дифференциальных уравнений.- М.: ИЛ, 1958.

[2.8] Арнольд В. И. Обыкновенные дифференциальные уравнения. - М.: Наука, 1975.

[2.9] Арнольд В. И. Дополнительные главы теории обыкновенных дифференциальных уравнений.- М.: Наука, 1979. .{2.10] Brunovsky Р.: Рокгоку mat. fyz. astr. 18 (1973), 271.

;2.11 Brunovsky P., Medved M.: Pokroky mat. fyz. astr. 27 (1982) 74. 2.12] Irwin M. C: Smooth Dynamical Systems. Academic Press, London, 1980. 2.13 Boruvka 0.: Zaklady teorie matic. Academia, Praha, 1971. 2.14] Schmidtmayer J.: Maticovy pocet a jeho pouziti v technice. SNTL, Traha, 1967.

[2.15 Гантмахер Ф. P. Теория матриц.- M.: Наука, 1966. [2.16] Carr J.: Applications of Centre Manifold Theory. Springer, New York, 1981.

[2.17] Marsden J. E., McCracken M.: The Hopf Bifurcation and its Applications. Springer, New York, 1976. Имеется перевод: Марсден Дж., Мак-Кракен М. Бифуркация рождения цикла и ее приложения.-М.: Мир, 1980.

2.18] Шошитайшвили А. Н. Труды семинара им. И. Г. Петровского 1 (1975). 2.19] Abraham R., Robbin J.: Transversal Mappings and Flows. W. A. Benjamin, Inc., New York, 1967. 2.20] Арнольд В. И. Успехи мат. наук 28, 5 (1972), с. 119. 2.21 Богданов Р. И. Труды семинара им. И. Г. Петровского, 2 (1976), с. 23-37.

[2.22] Gottschalk W., Hedlund G. А.: Topological Dynamics, AMS Colloquium publications, V. 36, Providence, R. I. 1955.

[2.23] looss G.: Bifurcation of Maps and Applications. North-Holland Publ. Сотр., Amsterdam, 1979.

[224] Nitecki Z.: Differentiable Dynamics, MIT Press, Cambridge, Massachusetts and London, England, 1971. [Имеется перевод: Ннтецкн 3. Введение в дифференциальную динамику. - М.: Мир, 1975.]

[225] Brunovsky Р.: Commun. Math. Univ. Carolinae 11 (1970), 22 (1971).

Здесь f(a) = f(6) = 0, т.е. имеются пространственно однородные стационарные состояния и(2, t) = а u(z, /)= b.-Прим. ред.

[2.26] Странные аттракторы. Сборник переводов под редакцией Я. Г. Сниая>

н Л. П. Шильннкова. - М.: Мир, 1981. [2.27] Оселедец В. И. Труды Московского математического общества 19

(1968), с. 179.

[2.28] Былов Б. Ф. н др. Теория показателей Ляпунова и ее приложения, к вопросам устойчивости. - М.: Наука, 1966.

[2.29] Немыцкий В. В., Степанов В. В. Качественная теория дифференциальных уравнений.-М.: Гостехиздат, 1949.

[2.30] Шильников Л. П. Теория бифуркаций и модель Лореица. Дополнение И в русском переводе [2.17].

;2,31] Smale S.: Bull. AMS 73 (1967). 747.

2.32] Henry D.: Geometric Theory of Semilinear Parabolic Equations. Lect.,

Notes in Math. 840. Springer, Berlin, 1981. [2.33] Satttinger D. H.: Group Theoretic Methods in Bifurcation Theory. Lect..

Notes in Math. 762. Springer, Berlin 1979. 2.34] Ruelle D.: Arch. Rat. Mech. An. 51 (1973), 136.

2.35] Sikorski R.: Rachunek rozniczkowy i calkowy. PWN. Warszawa, 1969.. 2.36J Jarnik v.: Differencialni poeet II. Academia, Praha, 1984.

[2.37] Nirenberg L.: Topics in Nonlinear Functional Analysis, Courant Inst, of Math. Sci., New York, 1973. [Имеется перевод: Ниреиберг Л. Лекции по иелииейиому функциональному анализу. - М.: Мир, 1977.]

[2.38] Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа. - М.: Наука, 1968. - 496 с.

[2.39] Kato Т.: Perturbed Linear Operators, Springer, Berlin. 1980. [Имеется, перевод предыдущего издания: Като Т. Теория возмущений линейных, операторов.-М.: Мир. 1972.]

[2.40] Taylor А. Е.: Introduction to Functional Analysis. J. Wiley, New York... 1958.

;2.41] КПг A.: Aplikace matematiky 28 (1983). 335.

2.42] Guckenheimer J.: Multiple Bifurcation Problems of Codimension Two..

Preprint University of California, Santa Cruz, 1979. [2.43] Col et P., Eckman J. P.: Iterated Maps on the Interval as Dynamical

Systems. Birkhauser, Boston, 1980. ;2.44l Nagy J.: Vybranfe partie z modern! matematiky. SNTL. Praha. 1976.. 2.45] Спивак M. Математический анализ иа многообразиях. - М.: Мир,.

1968.

[2.46] Nagy J.: Stabilita feSenf obyeejnych differencialnfch rovnic SNTL Praha, 1980.

[2.47] Шильииков Л. П. Математический сборник, т. 81(123), № 1, с. 92..

Глава 3

ВЕТВЛЕНИЕ СОСТОЯНИЙ РАВНОВЕСИЯ НА ДИАГРАММЕ РЕШЕНИЙ

в предыдущей главе мы сделали попытку познакомить читателя с основными понятиями теории динамических систем, -а также со связанными с ними явлениями бифуркаций.

В этой главе мы рассмотрим методы, позволяющие исследовать поведение стационарных решений систем дифференциальных уравнений в зависимости от параметра в окрестности точек ветвления. Такого рода анализ тесно связан с построением так называемой диаграммы решений, которое приходится проводить численно. При этом сами численные алгоритмы рассматриваются в гл. 5. Р1

3.1. ДИАГРАММА СТАЦИОНАРНЫХ РЕШЕНИЙ

Анализ стационарных решений (состояний равновесия) одно-параметрических семейств дифференциальных уравнений приводит к необходимости исследования множества решений следующей системы:

fiixu Х2, х„, а) = 0,

/2(1, Х2, Хп, а) = 0, J

f,j(xi, Х2, ..., х„, а) = 0.

В дальнейшем мы будем предполагать, что функции fi{X], ... ..., Xrt, а), j = 1, 2, ..., п, достаточно гладкие, а - вещественный параметр, а xi, Хг, Хп - неизвестные. Систему (3.1.1) .можно кратко записать в виде

f(x, а) = 0.

, (3.1.2)

Множество всех решений системы (3.1.1) обозначим S (f):

S(f) = {(x, a)eR XR, f(x, а) = 0}. (3.1.3>

Множество S (f) обычно представляет собой объединение нескольких кривых в R * , хотя может включать в себя и отдельные изолированные точки (рис. 3.1).

При п > 1 множество S (f) удобно изображать на двумерной плоскости. Такое двумерное представление множества S(f) мы будем называть диаграммой стационарных решений. При этом мы обыкновенно проектируем множество S.(f) на выбранную*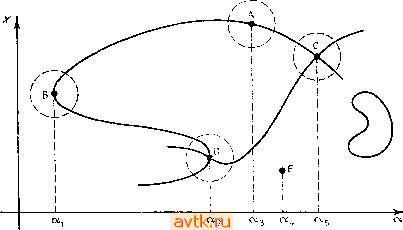

Рис. 3.1. Множество S (f).

плоскость Xi - а. При проектировании может оказаться, что на двумерной картинке имеет место пересечение кривых, хотя на самом деле в R * эти кривые не пересекаются.

Точки фактического и кажущегося пересечения кривых из: S (f) на диаграмме решений мы можем различать способом, показанным на рис. 3.2а,Ь. В дальнейшем последовательных различий между множеством S (f) и диаграммой стационарных, решений проводиться не будет; из контекста всегда будет ясно, какой из этих объектов имеется в виду.

Дадим теперь формальную классификацию точек множества S (f), начав со случая п==1. В этом случае множество решений S(f) можно изобразить на плоскости х - а (рис. 3.1).

1. Предположим, что {Xq, Oq) е S(/) и пусть

{хо, ао)ФО.

(3.1.4)

Тогда согласно теореме о неявных функциях существуют е > О и единственная функция g{a) {g{ao) = Xo), такая что f{g{a),a) = 0 для всех ае(ао -е, о + е). При этом множество S(f) в окрестности точки {хо,ао) задается графиком функции g.

Точку {xq, ao)eS(f), для которой выполнено условие (3.1.4), мы называем регулярной точкой. Как видно из рисунка, большинство точек кривой принадлежат именно к этому типу.

Рис. 3.2. Точки пересечения на диаграмме решений. 2. Пусть теперь в точке {xq, Oq) е S (f)

{хо, ао) = 0.

(3.1.5)

В данном случае мы не можем воспользоваться теоремой о неявных функциях. Однако если

{хо, Оо) Ф О,

(3.1.6)

то, поменяв x и а местами, можно построить в окрестности точки (а'о, ао) функциональную зависимость а = а(л;), ао = = ао{хо). Из соотношения (3.1.5) следует, что а'(д^о) = 0. На рис. 3.1 такой точкой является точка В.

Точку {xq, ao)eS(f), в которой одновременно выполняются условия (3.1.5) и (3.1.6), а производная da/dx меняет знак , мы называем (простой) точкой поворота. 1®

При переходе а через значение ао происходит бифуркация: появляется или исчезает пара решений. Значение ао мы называем бифуркационным значением параметра.

3. Если в точке (xq, Oq) S (f)

{хо, ао) = -(о, ао) = 0.

(3.1.7)

то точка (а'о, ао) называется сингулярной точкой множества S(f). Обозначим через a{f) множество всех точек поворота и

Чтобы производная а'{х) меняла знак в этой точке, достаточно выпол-нения условия {df/dx) (хо, ао) ¥= 0.

сингулярных точек множества S (f). Точки множества а(/) мы? называем критическими точками S(f). Критические точки разбивают множество S(/) на ветви стационарных реш.ений\ Каждая ветвь состоит из регулярных точек и определяет однозначную зависимость х{а).

Во всякой точке поворота заканчиваются две ветви решения.. В особой точке могут оканчиваться несколько ветвей (в точке С на рис. 3.1 -четыре).

Замечание. Множество S(f) в общем случае состоит из нескольких кусков - компонент связности (на рис. 3.1 их три)-

Может случиться, что какая-либо компонента представляет собой замкнутую кривую, не имеющую самопересечений.. Такую компоненту множества S(f) мы будем называть изолой. Изола состоит из двух (или более) ветвей, разделенных точками поворота.

3.2. ВЕТВЛЕНИЕ В ТОЧКАХ БИФУРКАЦИИ. ОДНОМЕРНЫЙ СЛУЧАЙ

Рассмотрим уравнение

fix, а) = 0, xR. (3.2.1>

Далее, пусть (д;*, а') е S(f) (т. е. /{х', а) = 0) и

{х\ а) = -{х', а-) = 0. (3.2.2>

Предположим также, что по крайней мере одна частная производная второго порядка от функции / в точке (х*, а*) отлична от нуля.

Разложим функцию f с помощью формулы Тейлора в окрестности точки {х*,а*). Учитывая, что f{x*,a*) = 0, а также соотношения (3.2.2), получаем

fix, а) = [А(х-хУ-\-2В(х-х')(а-а') +

, +С{а~аУ] + о[{х-хУ + {а-аУ] = 0, (3.2.3>

где

л df{x*,a*) d df {х', а*) df (х*, а*)

дХ , о- QQ . 1>-

Разделим соотношение (3.2.3) на {а - а*у или {x - x*Y и осуществим предельный переход {х,а){х', а), {х,а)

Иначе говоря, ветви - компоненты связности множества S{f)\a(f).- Прим. ред.

S(f), см. [3.1]. При этом мы получим уравнение

dx da

+ С = 0,

или

(3.2.4)

(3.2.6)

Здесь dx/da - угловой коэффициент касательной к дуге, проходящей через точку {х*,а*), если мы рассматриваем х как функцию а, или же da/dx - угловой коэффициент касательной, если мы считаем а функцией от х.

аг а. а.

Рис. 3.3. Поведение решений в окрестности критической точки.

Рассмотрим теперь уравнения (3.2.4) и (3.2.5).

Случай I. Л 0. Тогда решение уравнения (3.2.4) имеет вид

fdx\ ... ~В±л/В^~АС

Обозначим D = - АС. Если D < О, то точка (д^,а*) является изолированной точкой множества S(f) (из нее не выходит ни одна кривая). Если же D > О, то в этом случае уравнение (3.2.4) имеет два вещественных решения - это означает, что в окрестности точки {х*, а*) множество S (f) состоит из двух пересекающихся дуг. Или: в точке {х*, а*) сходятся четыре ветви стационарных решений (см. рис. 3.3а).

Случай II. Л=0, СфО. Тогда уравнение (3.2.5) имеет два решения

/ rfa \ da\ 2В

в этом случае множество S (f) в окрестности точки {х*,а*) также состоит из двух пересекающихся дуг (рис. 3.36). Одна из них имеет в этой точке вертикальную касательную: {х*,а*) - точка поворота для этой ветви. Такой случай отвечает бифуркации типа вилка и обычно встречается в системах, обладающих симметрией.

3.3. ВЕТВЛЕНИЕ В ТОЧКАХ БИФУРКАЦИИ. МНОГОМЕРНЫЙ СЛУЧАЙ

В этом параграфе мы вновь обратимся к анализу системы (3.1.1), см. [3.2]. Пусть (х*, a)eS(f), т. е.

(3.3.1)

Введем обозначения

(3.3.2)

(3.3.3)

При этом все частные производные в формулах (3.3.2) и (3.3.3) вычисляются в точке (х*,а*).

Случай 1. DetJ=iO. Если detJ=iO, то к системе (3.1.1) можно применить теорему о неявных функциях, согласно которой для всех а, взятых в некоторой окрестности U(a*), существует однозначная зависимость

X = X (а), f(x(a), а)0

для всех aU{a*). Таким образом, через точку (х*, а*) проходит только одна ветвь решений системы (3.1.1). Точку (х*, а*), для которой выполнено условие

detJO, (3.3.4)

мы будем называть регулярной точкой.

Случай П. Det J==0 и ранг расширенной матрицы J равен п: rank(J) = n. В этом случае, заменив^ один из столбцов матрицы J последним столбцом матрицы J, можно добиться того, чтобы полученная матрица имела ранг п.

Для удобства записи предположим, что заменен первый столбец матрицы J (этого всегда можно добиться с помощью подходящей нумерации столбцов), причем полученная матрица

Г dfi dfi df,

dfn dfn

(3.3.5)

дх2дхп -

имеет ранг п, т. е. detJaTO.

Тогда, аналогично случаю I, к системе (3.1.1) можно вновь применить теорему о неявных функциях, с той лишь разницей, что роль а играет теперь переменная xi. Таким образом, можно утверждать, что существуют функции Xj = Xjixi), j = 2, п, и a = a{xi), определенные в некоторой окрестности U (л:*), такие, что

х^ (х*) = х], 1 = 2, п, а (х') = а*, f{xi, Xiixi), x{xi), а(д;,)) = 0

для всех XjeU(jCi). Можно показать, что

(3.3.6)

Тогда, если da/dxj < О, функция a(.ti) имеет в точке х\ максимум - это означает, что при а > а* пара стационарных решений исчезает. Если же da/dx О, то функция a{xi) в точке имеет минимум и, значит, прн а > а* возникает пара стационарных решений. Такую точку {х*, а*) мы будем называть точкой поворота.

Если ранг матрицы J(x*, а*) меньше п, то точку (х*, а*) называют сингулярной точкой множества S(f).

Случай III. rank(J(x*,a*)) = n-1.

Предположим, что rank(J) = п- 1 (этим случаем мы и ограничимся). Тогда нз матрицы J можно выбрать матрицу Ji порядка п-1, определитель которой отличен от нуля. Для упрощения записи будем предполагать, что матрица Ji получается из матрицы J вычеркиванием первого столбца н последней строки. Таким образом,

dfr df,

дхо

дХп

L дХ2

дХп

(3.3.7)

detj,(x*, а)фО. (3.3.8)

Рассмотрим первые п-1 уравнений системы (3.1.1). Условие (3.3.8) позволяет применить к этой системе теорему о неявной функции. Из нее следует, что существуют функции

Xi = (fi{x а), 1 = 2, 3, и, (3.3.9)

определенные в некоторой окрестности U точки {х\, а), такие, что для (Ху, а) е и имеют место условия

* = К' *) = 2, 3, ..., и

и

fjixi, ф2(1. а). а), а)0, (3.3.10)

где / = 1, 2, ..., и - 1.

Подставим функции (3.3.9) в последнее уравнение системы (3.1.1), введя при этом обозначение

F{xi, a) = f{xi, (p2{xi, а), фз(д;1, а), (pixi, а), а). (3.3.11а) Мы получим

Fixi, а) = 0. (3.3.11b)

Теперь можно исследовать уравнение (3.3.11) с помощью методов, описанных в § 3.2. Таким образом, нам удалось (исходя из заданных предположений о ранге матрицы J) свести {n-j- 1)-мерную задачу к двумерной.

Можно убедиться, что в рассматриваемом случае, когда rank(J)= п- 1,

ЖГ *) = Ж-К' *) = 0- (3.3.12)

Таким образом, сингулярной точке (х*,а*) множества S{f) в R отвечает сингулярная точка множества S{F) в Rl

Из уравнения (д:!, а) = 0 (3.3.11) можно так же, как это сделано в § 3.2, найти угловые коэффициенты касательных

к ветвям S {F) (т. е. вычислить значения в точке {х\, а)). Затем с помощью формулы

da--Ж + Ж' /-2. 3, л (cS.cS.lcS)

можно найти направление ветвей S (f), проходящих через точку (х*,а*) в R +. Это есть итог наших вычислений.