Фейгенбаум впервые отметил следующее явление (см. замечание в конце этого пункта). Пусть при а < 1 система (2.5.4) имеет устойчивое периодическое решение с траекторией уа-При а = tti происходит бифуркация удвоения периода, причем траектория Уа при а > ai теряет устойчивость и от нее (при а > tti) ответвляется траектория у'а' с двойным периодом. Далее, при а = аг происходит бифуркация удвоения периода для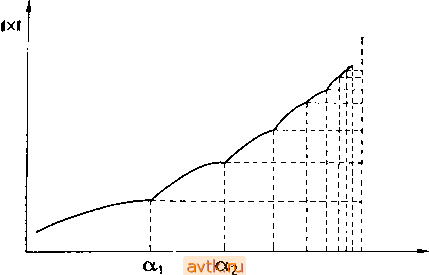

Рис. 2.37. Последовательность бифуркаций удвоения периода.

Траектории Уа- Затем этот процесс продолжается, и мы получаем бесконечную последовательность значений параметра 1, аг, ..., при которых происходят бифуркации удвоения периода (рис. 2.37).

Фейгенбаум показал, что для последовательности {a/}/li имеет место соотношение

= 4,6692016 ....

(2.5.5)

Число в правой части формулы (2.5.5) представляет собой универсальную постоянную, одинаковую для всех уравнений вида (2.5.4), у которых при увеличении параметра возникает вышеописанный каскад бифуркаций удвоения периода и которые удовлетворяют еще некоторым дополнительным условиям. Из

формулы (2.5.5) вытекает существование конечного предела вида

lim а, = а^. (2.5.6)

В результате описанного каскада бифуркаций возникает хаотическое множество, поскольку при а-а в некоторой области фазового пространства возникает бесконечно много неустойчивых периодических траекторий. Между этими траекториями блуждают остальные траектории, которые вместе с первыми образуют хаотическое инвариантное множество системы (2.5.4).

Замечание. Строго говоря, описанное явление было обнаружено Фейгецбаумом при исследовании поведения неподвижных точек итераций fa одномерного отображения / : [О, 1]-[0, 1] (например, faix)= ах{1 - х)) в зависимости от изменения параметра а.

С помощью отображения Пуанкаре бифуркационные процессы для отображения fa можно переформулировать для уравнения (2.5.4). При этом отображение ! можно рассматривать как проекцию отображения Пуанкаре на некоторую координатную ось в сечении S.

Указанный переход от описания явлений бифуркации для неподвижных точек итераций f к описанию бифуркационных процессов для фазового потока в окрестности замкнутой траектории с математической точки зрения не является строгим; скорее речь идет здесь об эвристических рассуждениях. С другой стороны, имеется много численных экспериментов, которые указывают на существование описанного выше каскада бифуркаций удвоения периода и определенную закономерность в поведении последовательности а/ (см. § 5.8).

2.6. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ

В гл. 6 будут описаны численные методы, используемые для нахождения точек бифуркации стационарных решений дифференциальных уравнений с частными производными (УЧП) параболического типа и, в частности, уравнений типа реакция - диффузия .

Последующее изложение призвано облегчить понимание этих бифуркационных явлений. Мы покажем, как можно перенести некоторые методы теории ОДУ на уравнения с частными производными параболического типа. Ради простоты мы огра-

ничимся рассмотрением одного уравнения вида

ди I 1 / \

(2.6.1)

где u = u(z,t) есть функция времени t и одной пространственной переменной z.

Рассмотрим, в частности, трубчатый (цилиндрический) реактор, учитывая из его размеров только длину (т. е. пренебрегая зависимостью всех величин от радиальной координаты г и угловой 6. - Ред.). Если уравнение (2.6.1) описывает процессы в таком реакторе, то функцию u{z,t) можно интерпретировать как концентрацию некого вещества в момент t в сечении с координатой z (рис. 2.38).

Рис. 2.38. Профили концентрации.

Пусть общая длина реактора равна L. Тогда при фиксированном t функция u(z, t) представляет собой функцию переменной z, определенную на промежутке [0,1]. График этой функции мы называем профилем концентрации в момент t. Изменение профилей концентрации в зависимости от времени описывает временную эволюцию данной системы.

Обычно для уравнения (2.6.1) задаются граничные и начальные условия. Начальное условие имеет вид

u(z, 0) = ф(г), ге[0, L]; (2.6.2)

оно задает распределение концентрации в момент времени / = 0. Граничные условия для уравнения (2.6.1) будут рассмотрены в следующем пункте.

2.6.1. Фазовое пространство уравнения (2.6.1)

В первых пяти параграфах этой главы мы рассматривали системы, состояние которых в данный момент времени t можно описать с помощью набора п чисел х() = (a;i(/), ...

Xn{t)). Фазовым пространством такой системы является пространство R или его часть, а эволюцию системы во времени можно описать движением фазовой точки по соответствующей траектории.

В случае упомянутого выше трубчатого реактора состояние системы в момент времени t описывается функцией, заданной на промежутке [О, L].

Следовательно, фазовым пространством уравнения (2.6.1) является пространство функций, определенных на промежутке [О, L], или его часть. Точки этого фазового пространства суть функции.

Функцию u{z,t) двух переменных z, t можно рассматривать как отображение, которое каждому / О ставит в соответствие функцию ( )= ( ,/) переменной г. Тем самым мы получаем некоторую кривую в подходящем образом выбранном пространстве функций. Эту кривую можно назвать траекторией уравнения (2.6.1). Введенное выше пространство функций в дальнейшем мы будем обозначать символом Е. При этом правую часть уравнения (2.6.1) можно рассматривать как оператор на пространстве Е, т. е. отображение F: Е->-Е.

Пример. Положим в уравнении (2.6.1) f{u)=u{\ - u), Р = I. Тогда правая часть (2.6.1) ставит в соответствие, например, функции u(z) = sinnz функцию

F (ы (z)) = (sin nz) -f sin z (1 - sin nz) -

= -jt sin Jtz -f sin nz cos nz.

Если рассматривать функцию u{z,t) как кривую в пространстве Е. т. е. как отображение t-u* (u*(z) = u{z,t)), то частную производную -(z, t) можно представить следующим образом:

° л- о

= lim

т. е. как вектор, касательный к кривой tuK

Уравнение с частными производными (2.6.2) можно теперь записать в виде обыкновенного дифференциального уравнения

= F( ), (2.6.3)

фазовым пространством которого является бесконечномерное функциональное пространство Е.

Пример 2.10. Рассмотрим дифференциальное уравнение

ди д^и

dt ~ dz

(2.6.6)

с граничными условиями вида

и {О, t) = u{n, 0 = 0. (2.6.7)

Стационарными решениями уравнения (2.6.6) являются решения обыкновенного дифференциального уравнения

ы (Z) = О, (2.6.8)

т. е. функции вида и{г)- аг-\-Ь, где а, b суть произвольные постоянные. Из этих функций мы должны выбрать те, которые удовлетворяют граничным условиям (2.6.7), т. е. условиям ы(0) = ы(я) = 0. Отсюда а = 6 = 0: единственным стационарным решением уравнения (2.6.6), которое удовлетворяет условиям (2.6.7), является функция и{г) = 0.

5 М. Холодниок и др.

Для уравнения (2.6.3) (а тем самым и для уравнения (2.6.1)) можно использовать большинство результатов, представленных в §§ 2.1-2.5.

Если к уравнению (2.6.1) добавлены граничные условия, например условия вида

и (О, t) = u{L, 0 = 0 (2.6.4)

для любых tO, то вместо пространства Е мы должны взять подпространство

0 = {иеЕ, и(0) = и(1) = 0}.

Это подпространство будет фазовым пространством уравнения (2.6.3), т. е. уравнения (2.6.1) при условиях (2.6.4).

2.6.2. Устойчивость стационарного решения

Если решение u = u{z,t) уравнения (2.6.1) не зависит от времени, то мы называем его стационарным решением. Профили концентрации стационарного решения не зависят от времени.

Стационарному решению Uo{z) уравнения (2.6.1) отвечает состояние равновесия уравнения (2.6.3): для него выполняется условие

F(ao) = 0. (2.6.5)

Соотношение (2.6.5) представляет собой обыкновенное дифференциальное уравнение Du + f ( о) =

После уточнения смысла предельного перехода в (2.6.9) (ввбдеиня иор-йы или расстояния в пространство Dq) сказанное близко к определеиню асимптотической устойчивости (см., например, [2.8]). -Ярил. ред.

Обратимся теперь к вопросу устойчивости стационарных решений дифференциальных уравнений в частных производных. В абстрактной записи (2.6.3) речь идет об устойчивости положений равновесия уравнения (2.6.3). Это означает, что стационарное решение uq{z) уравнения (2.6.1) является устойчивым лишь в том случае, если для всякого решения u{z,t) уравнения (2.6.1) с начальным условием (z, 0) = ф(2), где функция ф(2) достаточно близка к функции uo{z) в пространстве D, оказывается выполненным соотношение

lim и (z, t) = о (z) (2.6.9)

для любых ze[0, L]

Иными словами, профили концентрации решения u{z,t) сходятся при t--\-oo к графику стационарного решения Uo{z).

Устойчивость положений равновесия уравнения (2.6.3) можно определять так же, как и для обыкновенных дифференциальных уравнений. Именно, мы находим собственные числа линеаризованного уравнения, и если эти собственные числа располагаются слева от мнимой оси, то соответствующее состояние равновесия устойчиво. Этот подход продемонстрируем на примере.

Пример 2.10 {продолжение). Оператор ¥{и) = cPu/dz в правой части уравнения (2.6.6) является линейным и можно непосредственно найти его собственные числа. Напомним, что число ХеС является собственным числом линейного оператора F,

если существует не равная нулю функция и е D , для которой выполняется соотношение F( ) = Xu, т. е. функция u{z) представляет собой решение обыкновенного дифференциального уравнения

м Я = 0 (2.6.10)

с граничными условиями вида

(0) = (зх) = 0.

Оператор F имеет в данном случае только вещественные собст-вейные числа. При Я^О решение уравнения (2.6.10) записывается в виде

и (z) = c,ev -f с^е^-, с Cj е R.

Поскольку должны выполняться условия и(0) = и(я) = 0, то Ci = C2 = 0 и, следовательно, функция тождественно равна нулю. Таким образом, оператор F{u) = du/dz на пространстве Do не имеет неотрицательных собственных чисел.

При Л<0 решением уравнения (2.6.10) является функция

и (г) = Ci cos Vl Я IZ -f с2 sin Vl 12-

Из условий и(0) = и(я) = 0 следует, что д|Я|=, т. е. что значения

h = -k\ А; = 1, 2, ...

суть собственные числа нашего оператора.

Итак, все собственные числа располагаются слева от мнимой оси, и, следовательно, стационарное решение u(z) = О уравнения (2.6.6) устойчиво.

2.6.3. Периодические решения уравнения (2.6.1).

Бифуркация Андронова - Хопфа для уравнений с частными производными

Решение u(z,t) уравнения с частными производными (2.6.1), удовлетворяющее условию

u(z, t+T) = u(z, t) (2.6.11)

при любом fO и ze[0, L], мы называем периодическим; число Г > О есть период этого решения. Периодическому решению уравнения (2.6.1) отвечает замкнутая траектория уравнения (2.6.3) в фазовом пространстве Do (см. п. 2.6.1).

Положения равновесия уравнения (2.6.3) могут претерпевать бифуркации точно так же, как и положения равновесия обыкновенных дифференциальных уравнений. В частности, в случае бифуркации Андронова-Хопфа от положения равновесия уравнения (2.6.3) ответвляется замкнутая траектория; это означает, что от стационарного решения уравнения (2.6.1) ответвляется периодическое решение этого уравнения. Условия возникновения бифуркации Андронова - Хопфа для уравнений с частными производными аналогичны соответствующим условиям для ОДУ (см. § 2.3).

Рассмотрим однопараметрическое уравнение типа (2.6.3), которое мы запишем в виде

= F(u\ а).

2.6.4. Волновые решения уравнений с частными производными

Попытаемся выяснить принципиальные особенности волновых решений на том же примере одного дифференциального уравнения

-D + f{u) (2.6.12)

без граничных условий (рассматривая его при tO и е(-оо,4-оо)).

Решение и(г, t) будем искать в виде

и (г, t) = cf>{z-ct) = (p(l). (2.6.13

Подставляя выражение (2.6.13) в уравнение (2.6.12), мы получаем для ф() обыкновенное дифференциальное уравнение 2-го порядка

-Сф = /)ф -Ь/(ф), = (2.6.14)

Перепишем уравнение (2.6.14) в виде системы двух уравнений, положив Xi = ф, д:2 = ф':

X, = л;

(2.6.15)

Фазовым пространством системы (2.6.15) является плоскость

Хи Х2.

> Здесь dv/dt - Ао- линеаризованное уравнение.

Если взаимно сопряженные комплексные собственные числа оператора') А = Р(ио. а) пересекают мнимую ось в точках ±i<a, то в этом случае от стационарного решения ио соответствующего уравнения с частными производными ответвляется периодическое решение, причем период этого решения асимптотически (при приближении а к критическому значению а*) равен Т = 2я/<й.

А) Волновое решение типа импульса

Предположим, что система (2.6.15) при некотором значении параметра с обладает гомоклинической траекторией, выходя-щей из точки (0,0) (рис. 2.39)

х(4о)=Ко)

Рис. 2.39. Гомоклиническая траектория системы (2.6.15).

Решение x() = (a;i(), л;2()), соответствующее этой траек--тории, удовлетворяет условию

lim х() = 0. (2.6.16)

График функции л;1() = ф() представлен на рис. 2.40. График функции u(z, О = ф() = ф(2-ct) как функции переменной z

Рис. 2.40. Решение Xi(l), соответствующее гомоклинической траектории.

перемещается со скоростью с вдоль оси z, причем при с > О -он движется вправо, а при с<.0 влево (рис. 2.41). Решение уравнения с частными производными (2.6.12) с таким поведением называется волновым решением типа импульса, или бегущей волной типа импульса.

Для этого необходимо, чтобы точка (О, 0) была положением равновесия, т. е. чтобы /(0)=0. Для исходного уравнения (2.6.12) это означает: .u{z,t)=0 есть решение. Точка (0,0) для системы (2.6.15) будет (невырожденным) седлом, если Г(0)< О- Для исходного уравнения (2.6.12) это означает: состояние покоя устойчиво. - Прим. ред.

В) Волновое решение типа фронта

Если система (2.6.15) при некотором с обладает гетероклинической траекторией (рис. 2.42), выходящей из состояния рав-

Рис. 2.41. Волновое решение типа импульса.

(Ь,0) Ai

Рис. 2.42. Гетероклиническая траектория системы (2.6.15).

Рис. 2.43. Решение XiiE,), соответствующее гетероклинической траектории

новесия х<>=(Ь,0) и заканчивающейся в состоянии равновесия х<)=(а, 0), то решение x() = (a;i(),a;2()), отвечающее-этой траектории, удовлетворяет соотношениям

lim х() = х , Ит х() = х().

Таким образом, для функции xi =ф() будут выполняться следующие условия:

Ит ф() = Ь, lim ц>{1) = а. (2.6.17>