Диффузионный поток jdi линейно зависит от градиентов концентраций:

jd< = - Z DikgradCk,

(4.3.3)

где s - число компонент. Комбинируя формулы (4.3.1) и (4.3.3), получаем

=div Dikgradc + fiicu с,), i = l, 2, s.

(4.3.4)

Здесь коэффициенты диффузии и взаимной диффузии.

Если положить в дальнейшем Z)ii = const и Оц = 0 при 1Ф1

Рис. 4.9. Одномерная двухкомпонентиая система типа реакция - диффузия .

И рассматривать только две компоненты реакции, считая при этом задачу одномерной, то соответствующие уравнения баланса можно записать в виде (см. рис. 4.9)

- = Т^()+(ьС2), (4.3.5)

= §(-)+Ь(СьС2). (4.3.6)

Здесь L - размер системы, 2(0, 1) -безразмерная координата и /1 = -D] (dci/dz), J2 = -D2(dc2/dz).

Анализ поведения систем типа реакция-диффузия для случая двух компонент представляет собой достаточно общую задачу. В дальнейшем мы будем использовать следующие обозначения: х = Си у = С2, Dx = Du Dy = Dz, / = /i, g = fr, яля искомых функций x(z, t) и y(z, t) имеем

~-4r + fix,y), (4.3.7a)

(4.3.7b)

Выбор начальных и граничных условий для системы (4.3.7) зависит от конкретной физической ситуации. В случае задания на границе рассматриваемой пространственной области постоянных значений концентраций мы будем говорить о граничных условиях 1-го рода (ГУ1), или условиях Дирихле:

2 = 0: xiO,t) = Xo, y(0,t) = yo, (4.3.8а)

2=1: xil,t) = xu y{\,t) = g,. (4.3.8b)

Важный частный случай ГУ1:

Хо = х, = х, д^ = д^=у, (4.3.9) где X и у представляют собой решение уравнений

fix, у) = О, g{x,y) = 0. (4.3.10)

При таких граничных условиях есть очевидное стационарное решение уравнений (4.3.7), однородное по пространству:

x{z)x, y{z)y. (4.3.11)

Другим часто встречающимся типом граничных условий яр-ляются условия 2-го рода (ГУ2, или условия Неймана)

г = 0, 1: f- = - = 0. (4.3.12)

Указанные условия характеризуют непроницаемость границ области для компонент х и г/. Тривиальное стационарное решение (4.3.11), очевидно, удовлетворяет и ГУ2.

Граничные условия 3-го рода (ГУЗ), которые описывают частичную проницаемость границ системы для компонент х я у, имеют вид

2 = 0: а^о li + хох = Y;.o. а^о % + Р^оУ = Yj,o. (4.3.13а)

2=1: a j-hP x = Y. a f-+M = Y,i. (4.3.13b)

Для всех трех типов граничных условий мы ввели здесь сокращения ГУ1, ГУ2 и ГУЗ, которые в дальнейшем (в данной главе и в гл. 6) будут часто использоваться для упрощения записи. Заметим, что система может иметь на своей левой и правой границах граничные условия различных типов. Так, например, если нас интересует симметричное относительно центра промежутка решение для ГУ1 (4.3.9), то мы можем рассмотреть это решение на половинном промежутке, т. е. для 2е[0, 1/2], причем в точке 2 = 0 мы задаем ГУ1, а в точке z = 1/2 ГУ2.

fe-f 1

L т

]: (г=)=х(ф(г)), 0<fe</n-l,

(4.3.17)

S М. Холодннок и др

Начальные условия для системы (4.3.7) имеют вид

t = 0: X (г, 0) = Хо (г), у (г, 0) = Уо (z) (4.3.14)

и описывают начальное распределение концентраций (концентрационные профили).

Уравнения (4.3.7) с приведенными выше начальными и граничными условиями, кроме изотермической системы типа реакция- диффузия , могут описывать также, к примеру, некоторые задачи экологии [4.42].

Рассмотрим теперь асимптотическое поведение уравнений (4.3.7) с граничными условиями типа ГУ2 для случая очень больших интенсивностей массопереноса [4.43]. При этом д^x/дz-0 и dy/dzO, в результате чего вместо уравнений (4.3.7) мы получаем систему, в которой пространственные градиенты концентраций отсутствуют:

= f{x,y), = g{x,y). (4.3.15)

Уравнения (4.3.15) описывают систему с идеальным перемешиванием (систему с сосредоточенными параметрами).

Положим теперь один из коэффициентов диффузии равным нулю. Это можно сделать в тех случаях, когда величины коэффициентов диффузии сушественно различаются между собой, либо какая-нибудь компонента системы связана (неподвижна). Тогда найденное решение упрошенной задачи может служить аппроксимацией решения исходной задачи. Например, если Dx Dy, то построенная таким образом аппроксимационная модель принимает вид

дх Dx д^х , г, ч -df-lXT + fi У^

ду , , (4.3.16)

= (л:, у).

Система (4.3.7) в случае задания ГУ2 обладает еще одной интересной особенностью. Зная решение x{z), y{z) на промежутке ее [О, 1] при заданном L, мы можем с помощью сложения профилей построить решение x{z), y{z) при L = mL, где т - натуральное число, воспользовавшись для этого следующим способом:

где функция ф(г) определена при [О, 1] как

ф(г) = г, если k четное,

, и (4.3.18>

ф{г)=1-г, если k нечетное.

Аналогичный подход - сложение решений - можно использовать и для периодических решений. Для того чтобы лучше уяснить себе смысл операции сложения решений , читателю рекомендуется изобразить этот процесс графически для т = 2..

4.3.1.1. Задача И. Система реакция - диффузия для кинетики типа брюсселятор

Если использовать модельную кинетику типа брюсселятор * (см. задачу 7), то функции f я g в уравнениях (4.3.7) принимают вид

f(x,y) = A-{B+l)x + xy, (P1I-I)

g (х, у) = Вх - х^у.

Тривиальное стационарное решение (4.3.11) в этом случае записывается как

x(z)A, y{z) = B/A. (Pll-2)

Роль параметров в этой задаче играют Dx, Dy, L, А, В.

4.3.1.2. Задача 12. Система реакция - диффузия , случай ЗН-кинетики

Если рассматривать распределенную систему с кинетикой, описываемой SH-моделью (см. задачу 4), то функции f я g в уравнениях (4.3.7) представляются в виде

fix, y)==aivo + xy)/il+xy)-xil+y), (Р12-1>

gix, y)xi + y)-6x. (Р12-2)

Решение системы уравнений f - g = 0, в отличие от модели типа брюсселятор , здесь может быть найдено только численно (при заданных значениях параметров а, б, vo > О, р, 7 > > 1). При этом в определенном диапазоне изменения параметров можно получить несколько решений. Как и выше, задачу 12 можно рассматривать с граничными условиями всех трех типов. Отметим, что данная задача имеет восемь параметров: Dx, Dy, L, а, 8, vo, Р, у.

4.3.1.3. Задача 13. Система реакция - диффузия в случае модели Майнхардта

Одной из наиболее известных моделей морфогенеза в настоящее время является модель системы реакция-диффузия с кинетикой типа активатор-ингибитор, предложенная Майн-хардтом [4.44-4.47]. Эта модель описывает пространственную дифференциацию ткани в процессе эмбриогенеза при почти Симметричных начальных условиях.

Модель описывается системой двух уравнений реакция-диффузия типа (4.3.7). Функции f и g- в данном случае имеют вид

f (х, у) = РоР + срх^/у -iix, (р13-1)

g{x, y) = cpx-vy. (pi3-2)

Величины рир' характеризуют здесь плотность источников для веществ, действующих как активатор и ингибитор, а ро, с, , с', V - положительные параметры. У этой системы существует единственное тривиальное решение х, у:

= PoP/t + cpv/cpV, (pi 3-3)

g = cpx/v. (pi 3-4)

Для задачи 13 можно использовать граничные условия всех трех типов - ГУ1, ГУ2 или ГУЗ. В данной задаче имеется 10 параметров: Dx, Dy, L, р, р', Ро, с, \1, с', V.

4.3.2. Задача 14. Трубчатый неизотермический реактор с аксиальным перемешиванием

Модель трубчатого реактора с аксиальным перемешиванием используется как для гомогенных, так и для гетерогенных (каталитических) реакторов ([4.48], [4.49]). В последнем случае полезна упрощенная, псевдогомогенная модель, основанная на предположении, что гетерогенную систему катализатор-реакционная смесь можно заменить гомогенной средой с некими эффективными характеристиками. Такая псевдогомогенная модель и формулируется в задаче 14.

Рассмотрим трубчатый реактор с теплопередачей через стенку (см. рис. 4.10). Будем считать, что реакционная смесь полностью перемешивается в радиальном направлении; тем самым мы будем рассматривать только продольные градиенты тсонцентраций компонент и температуры. Далее, предположим, что плотность потока компонент в продольном направлении описывается соотношением вида -~-De(dc/dt), аналогичным

закону Фика, где De - эффективный коэффициент диффузии,. с - концентрация компоненты.

Аналогично будем предполагать, что плотность потока тепла в продольном направлении задается соотношением вида -ke(,dT/dl), где ke - эффективный коэффициент теплопроводности.

Ъ^рг{Го-Г)=-ке-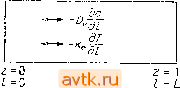

де дг dl dl

Рис. 4.10. Трубчатый реактор с аксиальным переносом тепла и массы; граничные условия типа Данквертса.

Предположим, далее, что в реакторе протекает реакция первого порядка, описываемая выражением для скорости реакции вида fe<x>cexp(-E/RT) (£ -энергия активации, i? -газовая постоянная) и с тепловым эффектом (энтальпией реакции) -АНт. Мы будем считать, что плотность теплового потока через стенку трубки определяется выражением 4U{T - Tc)/d, где U - соответствующий коэффициент теплопередачи, с? -диаметр трубки и Тс - температура теплообменной (например, охлаждающей) среды вне трубки.

Мы будем предполагать, что в реакторе имеется катализатор. Пусть плотность жидкости равна pf, а ее теплоемкость на единицу объема при постоянном давлении постоянна и равна Cps; плотность же катализатора равна ps, а его теплоемкость на единицу объема также постоянна и равна Cps. Тогда уравнения баланса массы и энергии можно представить в виде

p = D,-v-k{l-e)c ехр {-E/RT), (р14-1>

- PjPf dl

- (Г - Г,) + (i - 8р) (-АЯг) ехр i-ElRT). (р14-2)

Здесь т - время, ер - доля объема, занятая жидкостью, в V-(постоянная) скорость жидкости. Начальные условия еле-

Рем = -. Рен = -. У=Ж' (-КНЛс Ц\-йЛ

= yhfjf Da = -i feexp(-Y).

(PI4-6).-

ерР,Ср;-Ь(1-ер)РзСр,

4f/L

То RTo

Здесь у обозначает конверсию, © - безразмерную температуру, г - безразмерную координату, / - безразмерное время. Рем, Рен - числа Пекле для массы и тепла, у - безразмерную энергию активации, В - безразмерное адиабатическое повышение температуры. Da -число Дамкёлера, 3 - безразмерный коэффициент теплопередачи, ©с - безразмерную температуру охлаждающей среды и Le - число Льюиса.

В переменных (Р14-6) мы получаем систему уравнений

l=ptl*-f+DM.-.)exp, (Р14.7)

дэ 1 а^е д@

Le - =

Pi;7 li -17 + Dа (I - у) ехр - р (в - е.)

(Р14-8>.

дующие:

х = 0: с{1, 0) = сЦ1), Т{1, 0) = Т°{1). (PI4-3)

Пусть теперь на границе области выполняются граничные условия типа Данквертса (рис. 4.10) (см. [4.8])

т>0, 1 = 0: -De-j = u(Co-c),

(Р14-4)~

т>0, l = L: = §- = 0. (PI4-5)

Здесь Со и Го - концентрация и температура до входа в реактор. Введем следующие безразмерные переменные и параметры:

z = l/L, t = xv/Le у =1-с/Со, 0 =

С Граничными условиями

2 = 0;Ремг/=. Ренв = -, (PI4-9)

Данная задача имеет восемь параметров: Рем, Рен, у. В, Da, р, вс и Le. Заметим, что уравнения (Р 4-7), (Р14-8) отличаются от уравнений (4.3.7), описывающих систему типа реакция- диффузия , конвективными слагаемыми, а именно слагаемыми dy/dz и d@/dz. При этом граничные условия (PI4-9) принадлежат к типу ГУЗ, а условия (P14-I0) -к типу ГУ2.

Если аксиальное перемешивание осуществляется в слабой степеии (эффективные диффузия и теплопроводность очень малы, Рен->оо, Рем^оо), то вместо уравнений (Р14-7), (Р14-8) мы получаем гиперболические уравнения первого порядка, которые описывают трубчатый реактор идеального вытеснения:

+ f = Da(l-,)exp, (Р14-11)

+ = BDa{l-y)expj-m-@c). (Р14-12)

При этом условия (Р14-9) и (Р14-10) заменяются условиями 2 = 0: г/==0, е = 0. (Р14-13)

Соотношения (PI4-11) - (PI4-13) используются иногда для нахождения приближенного решения исходной задачи при больших значениях Рен, Рем.

4.3.3. Задача 15. Трубчатый неадиабатический реактор с аксиальным перемешиванием (двухфазная модель)

В случаях, когда температура и концентрация в объеме жидкости и на поверхности частиц катализатора резко отличаются, лриходится рассматривать двухфазную модель. В этой модели, кроме переменных Тис, характеризующих жидкость, вводятся температура поверхности катализатора Т* и концентрация на -его поверхности с*.

Здесь мы рассмотрим вариант этой модели, предложенный Лью и Амундсоном [4.50]. Помимо предположений, введенных при описании задачи 14, будем считать, что реакция протекает iHa поверхности катализатора. При составлении соответствующих уравнений баланса мы будем учитывать конвективный пере-

получим:

Pi;i-S--§- + -H(-®)-P(®-®=) = 0, (Р15-7

/м(со-г/)-Оа(1-со)ехру: = 0, (Р15-8)

/ (0-e)-SDa(l-co)exp = O. (Р15-9>

Граничные условия в безразмерном виде задаются соотношениями (Р14-9) и (Р14-10).

нос, межфазовый тепло- и массообмен, теплоотдачу стенок реактора. Потоки компонент реакции и поток тепла с внешней поверхности катализатора в жидкую реакционную смесь будем описывать с помошью коэффициентов массоотдачи и теплоотдачи, считая потоки пропорциональными разности концентраций с*-с или разности температур Т* - Т. При этом мы не учитываем перенос тепла и массы внутри частиц катализатора. Площадь внешней поверхности частиц катализатора, отнесен- ную к единице объема, обозначим через а.

Если рассматривать реакцию первого порядка, то для случая стационарного режима уравнения баланса вещества и энтальпии можно представить в форме [4.51]

De-v+kMc-c) = 0, (Р15-1)

- оСр -f + ha (Г-Т)-{Т-Т,) = 0. (Р15-2)-

Уравнения баланса массы и энтальпии на внешней поверхности катализатора принимают вид

kMc-c) + kexp(-)c = 0, (Р15-3>

Ла(Г -T)-k ехр (- с'(-АЯО = 0. (Р15-4>

Граничные условия на входе и выходе задаются соотношениями (Р14-4) и (Р14-5). Вводя безразмерные переменные по формулам (Р14-6) и, кроме того, полагая

. kaL j haL- cq - c* д t* - Гц /DiKr:v

/м = -, н = -, со = -, е = -(Р15-5).

(ю) = /м (со - г/) - Da (1 - со) ехр

н

в+5-(ш-</) н

= 0.

(Р15-11)

Таким образом, задача описывается системой двух дифференциальных уравнений (PI5-6) и (Р15-7) относительно неизвестных ч|)ункций г/(г) и @(z) (краевая задача) и одним нелинейным (алгебраическим) уравнением (Р15-11) для определения величины со. Функция Q{z) при этом выражается через y{z) и со по формуле (Р15-10). В общем случае данная задача имеет 9 параметров: Рем, Рен, /м, /н, В, Da, у, р и и представляет собой одну из проблем, в которых речь идет о совместном решении системы дифференциальных и алгебраических уравнений (см. также задачу (4.3.16) для случая установившегося режима).

-4.3.4. Задача 16. Неизотермическая модель внутренней диффузии в частице пористого катализатора

Большинство каталитических реакций протекает на пористых частицах катализатора. Процессы тепло- и массообмена внутри пористой частицы и на ее поверхности часто существенным образом влияют на результирующую скорость реакции. Поэтому анализ указанных процессов имеет большое практическое значение. Математические модели, описывающие взаимодействие процессов тепло- и массообмена с реакцией на пористом катализаторе, обычно рассматриваются для частиц трех геометрических форм: бесконечная пластина или одна пора, проходящая через частицу (а=0); бесконечный цилиндр (а = 1); и, наконец, шар (а =2). В дальнейшем параметр а будет определять собой форму частицы. Введем следующие предположения [4.11]:

1. Сложные процессы переноса внутри пористой структуры можно описать с помощью постоянных эффективных коэффициентов диффузии De и теплопроводности Яе.

Комбинируя (Р15-9) И (PI5-8), имеем

Э = в + В-у^Сю-г/). {Р15-10)

н

Воспользовавшись (Р15-10), исключим из соотношения (Р15-8) величину Э: