Невозможность асимптотической устойчивости периодического решения р(/) автономной системы очевидна: малое возмущение, состоящее в замене р(0) иа р(б), приводит к незатухающему эффекту (р(-Ьб)-р(0 ие стремится к 0). - Прим. ред.

ИЗ которого видно, что функция

z,(0 = p(0

есть периодическое решение уравнения в вариациях.

Критерий орбитальной устойчивости периодического решения

Пусть р() есть периодическое решение системы (2.3.10) и Pi = 1, р2, р -его мультипликаторы. Если 1р/< 1 при / = 2, .... п, то решение р() является асимптотически орби-тально устойчивым. 11

Замечание. Из того факта, что мультипликатор pi = 1, и из критерия устойчивости, приведенного в конце п. 2.3.4, следует, что периодическое решение не может быть асимптотически устойчивым по Ляпунову). Поэтому для периодических решений имеет смысл говорить лишь об орбитальной устойчивости.

2.3.6. Заключительные замечания

1. На практике нахождение мультипликаторов периодического решения проводится с помощью численных методов (см. п. 5.8.3).

2. Если мы исследуем периодическое решение 1-параметри-ческой системы дифференциальных уравнений

x = f(x, а), R , (2.3.13)

то его мультипликаторы будут функциями параметра а. Предположим, что при а<ао мультипликаторы Р2(а), рп{а) лежат внутри единичного круга (pi(a)= 1). Это означает, что периодическое решение является орбитально устойчивым.

При изменении параметра потеря устойчивости происходит в том случае, если один из мультипликаторов покидает единичный круг. В общем случае это может произойти одним из трех способов:

(1) Один из мультипликаторов пересекает единичную окружность в точке -fl.

(2) Один из мультипликаторов пересекает единичную окружность в точке -1.

(3) Пара комплексно-сопряженных мультипликаторов пересекает единичную окружность в точках е- , со Ф 2п/п, п=1,2, 3, 4.

Все эти три возможности изображены на рис. 2.30.

Можно доказать, что в случае (1) происходит бифуркация

рождения или исчезновения пары периодических решений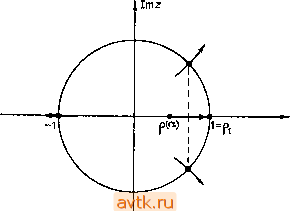

Рис. 2.30. Мультипликаторы в комплексной плоскости как функции параметров.

(см. рис. 2.22). В случае (2) имеет место бифуркация удвоения периода (см. рис. 2.23), а в случае (3) возникает инвариантный тор (см. рис. 2.24).

Замечание. В случае, когда система (2.3.13) обладает некоторой симметрией g и мы следим за g-симметричным решением, при условии типа (1) может произойти бифуркация с потерей симметрии (см. рис. 2.25).

2.4. ПРЕДЕЛЬНЫЕ МНОЖЕСТВА ТРАЕКТОРИЙ

2.4.1. Гетероклинические и гомоклинические траектории

Под гетероклинической траекторией системы х = f (х) мы понимаем траекторию, которая выходит из одного состояния равновесия Хо и входит в другое состояние равновесия системы xi (см. рис. 2.31). Точнее говоря, если существует точка Z е R , такая, что для решения z{t) системы x = f(x) имеют

Рис. 2.31. Гетероклиническая траек- Рис. 2.32. Гомоклиническая траектория, тория.

Гомоклиническая траектория представляет собой траекторию, которая выходит и входит в одно и то же состояние равновесия Xq (рис. 2.32). Если q)z(0 - решение, соответствующее этой траектории, то

lim (fг{t)= lim q)z(0 = Xo. (2.4.2)

Объединение гомоклинической траектории y{z) и одноточечной траектории {хо} дает нам замкнутую кривую, которая называется гомоклинной петлей.

2.4.2. Общие траектории

Для описания поведения общей траектории при t-+oo удобно ввести понятия а- и со-предельного множества данной траектории.

Определение 2.6. Пусть ф - фазовый поток уравнения х= =/(х) hy(xo)-его траектория.

(а) Точку Z е R мы называем со-предельной точкой траектории 7(хо), если существует последовательность вещественных чисел для которой

lim tk = + oo

место соотношения

lim q)z(0 = Xo и lim q)z(0 = Xi, (2.4.1)

TO траектория этого решения называется гетероклинической.

Замечание. На рис. 2.31 изображены три траектории: у(хо) = = {xq}-одноточечная, 7 (xi) = {xj - также одноточечная и у (z)- гетероклиническая.

И выполняется соотношение

lim qjfe, Xo)==z.

ft->-+oo

(2.4.3)

Множество всех ш-предельных точек данной траектории у обозначают а (у) и называют (л-предельным множеством траектории у.

(Ь) Точку а е R мы называем а-предельной точкой траектории 7(хо), если существует последовательность вещественных чисел {tk)k~u для которой

Ит /j = -оо

fe->-+oo

и выполняется соотношение

Ит q)(/fe, Хо) = а.

fe->- + oo

(2.4.4)

Множество всех а-предельных точек данной траектории у мы называем а-предельным множеством траектории у и обозначаем а (у).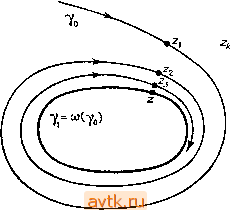

Рис. 2.33.

Замечание. С помощью введенных понятий гетероклиниче-скую траекторию можно определить следующим образом: траектория у гетероклиническая, если а(7)= {хо} и (j)(7)={xi}, где Хо, xi (xo=7xi) - положения равновесия системы. Аналогично, траектория 7 является гомоклинической, если а (7) = = (й(7)= {хо}.

С помощью а- и ш-предельных множеств можно визуализировать асимптотическое поведение решений дифференциальных уравнений (рис. 2.33). Так, например, на рис. 2.33 ш-пре-

ot >0 Q<a.2<a.i а.=а

Рис. 2.34. Возникновение гомоклинической петли Г.

(см. рис. 2.34). При а = 0 периодическая траектория превращается в гомоклинную петлю. Если теперь двигаться по рис. 2.34 справа налево (т. е. увеличивать а от 0), то мы увидим возникновение периодической траектории из гомоклинной петли. Механизм возникновения гомоклинной петли может быть и иным; например, состояние равновесия может возникнуть на замкнутой траектории.

Замечание. В окрестности гомоклинных петель в трехмерном или многомерном фазовом пространстве обычно существуют хаотические инвариантные множества (см. п. 2.5.2).

2.5. ПОКАЗАТЕЛИ ЛЯПУНОВА

Поведение траекторий в окрестности состояния равновесия для уравнения

x = f(x), xeR (2.5.1)

мы описываем с помощью собственных чисел матрицы линеаризации. Для описания поведения траекторий в окрестности замкнутой траектории служат ее мультипликаторы. Для исследования поведения траекторий в окрестности произвольной

дельным множеством траектории 70 является замкнутая траектория 71, т. е.

м (Yo) = Yi.

2.4.3. Возникновение гомоклинной петли

Механизм возникновения петли можно наблюдать в 1-пара-метрической двумерной системе дифференциальных уравнений

x = f(x, а), xeR2, ае[0, 1]. (2.4.5)

Пусть при ае(0, 1] система (2.4.5) имеет периодическое решение ра(0. траектория которого уа при а->-1-0 приближается к состоянию равновесия Хо, представляющему собой седло

траектории удобно использовать показатели Ляпунова, которые представляют собой аналоги мультипликаторов периодических траекторий.

2.5.1. Основные свойства показателей Ляпунова

Пусть Г(хо) - траектория уравнения (2.5.1), соответствующая решению р(0 = Фхо(0- Асимптотическое поведение траекторий, лежащих вблизи 7(хо), определяется поведением фундаментальной матрицы Ux (0 уравнения в вариациях для решения р(/). Показатели Ляпунова являются инструментом, служащим для описания асимптотического поведения матрицы

Рис. 2.35. Деформация параллелепипеда Р при движении вдоль траектории.

Рассмотрим п линейно независимых векторов bi, Ьг, ..., Ь„, выходящих из точки Хо. Выберем из них k векторов (1 Л^л), которые обозначим как ei = bip e2==bj2, tk = - bi. Векторы ei, e задают в фазовом пространстве R некоторый -мерный параллелепипед (см. рис. 2.35, где /г = 3) и определяют натянутое на них /г-мерное подпространство е^*.

Фазовый поток перемещает точку Xq за время t в точку fp (t); при этом векторы еь ег, ..., е^ отображаются на векторы и^ДОвр и^ДОСу которые в свою очередь образуют параллелепипед ф'(Р*). Нас будет интересовать изменение объема параллелепипеда Р*, точнее, отношение объемов ф'(Р*),иР*. Обозначим объем параллелепипеда Р* через HeiACaA ... ЛеЦ. Этот объем вычисляется следующим образом.

Здесь введево (стандартяое) определение того, как действует (при каждом t) преобразование <р' сдвига по траекториям x->-<Pj5(f) иа векторы, прикрепленные в точке хо. - Прим. ред.

В исходном определении (А. М. Ляпунова) берется верхний предел - Прим. ред.

> Это утверждение приобретает точный смысл после разъяснения того, что означает здесь с вероятностью 1 . - Ярил. ред.

Обозначим через (е/, е,) скалярное произведение векторов е, и С/, 1, j == \, 2, ..., k. Тогда

1е,л ... Ae, = [detA],

где матрица А = {ац), а,-,-= (Cj, Су), i, /= 1, k. Выражение II Ux (0 Ci Л ... Л Ux (/) Cfell обозначает объем параллелепипеда

Определение. Предел (если он существует)

ли. е )= ш 1п - :;-;У' (2.5.2>

<->+ос. t lliA л kW

называется fe-мерным показателем Ляпунова траектории Г(хо)-Этот показатель представляет собой меру скорости изменения объема параллелепипеда при его перемещении вдоль траектории Г (хо).

Условиями существования предела (2.5.2) мы здесь заниматься не будем'. Нетрудно показать, что Я(хо, е**) зависит лишь от подпространства е***, а не от конкретного выбора векторов базиса. Наиболее важная информация, касающаяся показателей Ляпунова, содержится в следующей теореме.

Теорема.

1. Одномерные показатели Ляпунова могут иметь не более п различных значений 2 п.

2. fe-мерные показатели Ляпунова могут иметь j различных

значений, причем каждый из них представляет собой сумму k одномерных показателей Ляпунова.

3. Если линейно независимые векторы Ьь ..., Ь„ выбраны случайным образом, то выражение в правой части формулы (2.5.2) с вероятностью 1 сходится к максимальному fe-мер-ному показателю Ляпунова 11.

Замечания

1. Рассмотрим понятие одномерного показателя Ляпунова несколько подробнее. Пусть ее R . Формула (2.5.2) при k=l принимает вид

К (Хо, е) = lim I In 11. (2.5.3)

Показатель Ляпунова (хо, е) описывает поведение траекторий, проходящих через точки хо + ее, 8<С 1, по отношению к траектории Г(хо) (см. рис. 2.36).

Если Л(хо, е) < О, то это означает, что указанные траектории приближаются к Г(хв) при /->-)-оо, а если Л(хо, е)>0, то удаляются. 11

Если в этом случае изменить начальное состояние хо на xo-f ее, 8< 1, то разность 4>х„+ее () ~х. W будет расти со временем с экспоненциальной скоростью: поведение динамической системы очень чувствительно к изменению начальных условий.

Г(Л'р) Xq

Мло,е)>0

/ее /та+ев)

Х(А'а,в)<0

Рис. 2.36. Поведение близких траекторий.

2. Если в формуле (2.5.3) положить e = f(xo), т. е. выбрать вектор, касательный кГ(хо), то вектор Uxo(Oe будет касательным все время: имеет место соотношение UJ/)f (Xo) = f (ф^(О)-Если векторное поле f(x) ограничено (f(x)</C для всех хе R ), то из (2.5.3) вытекает, что ; (хо, f (хо)) = 0. (Для того чтобы один одномерный показатель Ляпунова траектории Г(хо) был равен нулю, достаточно, чтобы функция f(x) была ограничена в некоторой окрестности ее ю-предельного множества.)

3. Второе утверждение теоремы мы проиллюстрируем на примере траектории в R. Согласно п. 1 этой теоремы, существует три одномерных показателя Ляпунова. Согласно п. 2 этой же теоремы, число двумерных показателей Ляпунова равно

2 ) = 3 и их можно найти с помощью одномерных показателей

Ляпунова:

= 1 -)- 2, 2 = 1 -)- 3, Яз = 2 + з!

трехмерный показатель Ляпунова будет всего один:

1 = -\- К2 -\- Кз.

1(2)

(2).

Если это множество не состоит из одной точки. - 77рмж. ред.

Л/г - Лтах тах

5. Одномерные показатели Ляпунова W) для стационарного решения (р()хо) связаны с собственными значениями ц; матрицы Якоби J = f(xo) соотношениями: Я/ = Ке(х/. Показатели A.<j для периодического решения р(0 периода Т выражаются через его мультипликаторы ц/:

я1 = -1п|ц,-.

2.5.2. Инвариантные множества

Множество М сг R мы называем инвариантным множеством дифференциального уравнения x = f(x), хе если любая его траектория, имеющая хотя бы одну общую точку с множеством М, целиком лежит в множестве М.

С простейшими инвариантными множествами потока ф(х) мы уже встречались в § 2.1-это были положения равновесия и замкнутые траектории.

Изучение свойств замкнутых инвариантных множеств проводится с помощью специальных методов, описание которых выходит за рамки данной книги. Ниже мы лишь кратко коснемся этой темы.

Определения

1. Замкнутое инвариантное множество М потока ф называется устойчивым (по Ляпунову), если для любого е>0 существует такое бе(0, е], что еслир(х, М)б, то р(ф,(0, М) 8 для всех t 0.

2. Замкнутое инвариантное множество мы называем аттрактором, если существует открытое множество [j s,

4. Третий пункт теоремы указывает на возможность вычисления всех одномерных показателей Ляпунова следующим способом. Выберем случайным образом базис bi, bz, , b п и затем с помощью ЭВМ найдем максимальные -мерные показатели Ляпунова, k= I, 2, п; обозначим их ....

Я^. Тогда все одномерные показатели Ляпунова можно определить с помощью следующих соотношений:

Л1 - Лтах>

л,2 - Лтах Лщах!

) Математики говорят траектория у всюду плотна в .9 . При наличии положительных показателей размерность М обычно оказывается дробной (см. [8*], [12*]). - 77рмл. ред.

такое, что для всякой точки х е U выполняется требование

Р(Фх(0, ),-о.

При этом множество U называется областью притяжения аттрактора s.

Некоторые авторы требуют дополнительно, чтобы в аттракторе существовала траектория у, которая его плотно заполняет Простейшими примерами аттракторов могут служить (асимптотически) устойчивые положения равновесия и устойчивые замкнутые траектории. У инвариантных множеств обычно изучают их зависимость от параметров, а также их внутреннюю структуру.

Инвариантное множество М называется внутренне неустойчивым (или хаотическим), если любая траектория, которая лежит в М, является неустойчивой по Ляпунову и имеет по крайней мере один положительный одномерный показатель Ляпунова, так что траектории, лежащие в М, разбегаются друг от друга с экспоненциальной скоростью. Мы будем требовать, кроме того, чтобы хаотическое множество плотно заполняла бы какая-нибудь траектория системы.

Определенную информацию на интуитивном уровне о ш-пре-дельном множестве данной ограниченной траектории у дают ее показатели Ляпунова. Так, если все показатели Ляпунова оказываются отрицательными, то можно ожидать, что М=©(у) состоит из одной точки - устойчивого положения равновесия. Размерность такого множества М равна нулю. Если один показатель Ляпунова равен нулю, а остальные отрицательны, то это указывает на наличие одномерного аттрактора, например устойчивого предельного цикла. Существование одного положительного показателя Ляпунова означает наличие двумерного аттрактора, и т. д. >

2.5.3. Явление Фейгеибаума

В этом пункте мы опишем один из возможных механизмов возникновения хаотического множества в фазовом пространстве.

Пусть у нас имеется однопараметрическая система дифференциальных уравнений

x = f(x, а), xeR , aeR. (2.5.4)