Укажем теперь некоторые возможности перевода модели в безразмерную форму. Отнесем все величины (переменные и параметры) к соответствующим характерным значениям. Прежде всего введем характерную температуру [4.10]

ш- , где а- .

В предельном случае адиабатического режима {11 = 0) а = 0 и Гщ = Го. Безразмерные концентрацию (ы) и температуру {у) определим так:

= , У = . (4.1.25)

-АО m

Введем безразмерные параметры: тепловыделение р, число Дам-кёлера Da, безразмерную э' ергию активации у.

о (-Ar)AO k(Tm)C% Е

СТ(х+а) =--F- Y = -. (4.1.25а)

Уравнения баланса (4.1.23), (4.1.24) после перехода к переменным (4.1.25) принимают вид

1-н-Ван ехр[у (l-у)] = 0, (4.1.26)

1-(/-(-рОаы ехр[у (l -у)] = 0. (4.1.27)

Умножая уравнение (4.1.26) на р и складывая результат с уравнением (4.1.27), нетрудно найти соотношение между безразмерной концентрацией и температурой:

= (l-f р-(/)/р. (4.1.28)

При подстановке этого соотношения в уравнение (4.1.27) мы получаем одно уравнение относительно безразмерной температуры у, описывающее установившийся режим работы реактора:

(/-l = p- Daf(r/), (4.1.29)

где

/(1/) = (1 + Р-у) ехр[у(1-1/(/)].

Безразмерное уравнение (4.1.29) описывает также химические системы, отличающиеся по физическим свойствам от рассматриваемой. Например, уравнения баланса массы и энтальпии, описывающие необратимую реакцию п-го порядка в частице пористого катализатора, в случае отсутствия значительных

градиентов концентрации и температуры внутри частицы имеют вид

cSx (сАо - са) - Урй (Г) d = О, (4.1.30)

Л5х (Го - Г) + (- АЯг) Урй (Г) d = 0. (4.1.31)

Здесь fee, /i - коэффициенты массо- и теплоотдачи на внешней поверхности частицы, Sx - площадь внешней поверхности частицы, Ур - объем частицы, а Сдо и Го - концентрация и температура в ядре жидкости, обтекающей частицу (т. е. в невозмущенной жидкости.- Яерев.). Вводя определения

из соотношений (4.1.30) и (4.1.31) мы вновь получаем уравнение (4.1.29).

Здесь число Дамкёлера Da есть отношение прореагировавшего количества вещества А (при Г = Гдо и с - сдо) к максимально возможному потоку массы этого вещества через поверхность.

Таким образом, одна безразмерная система уравнений описывает несколько различных с физической точки зрения задач.

4.1.2.4. Анализ числа стационарных режимов (решений уравнения (4.1.29))

Рассмотрим сначала эндотермические реакции, для которых (-АЯг)<0, р < 0. При этом левая часть уравнения (4.1.29) представляет собой монотонно возрастающую, а правая часть - монотонно убывающую функцию у. Таким образом, в данном случае может существовать не более одного стационарного состояния для любых значений критерия Da.

Рассмотрим теперь экзотермическую реакцию (-АЯг > О, Р >0). Перепишем уравнение (4.1.29) в виде

Пу)=- = -. (4.1.33)

Если предположить, что не(0;1), то из формулы (4.1.28) следует, что г/е (1; 1-f-Р). Если функция F(y) будет монотонно убывать на промежутке (1; 1+Р). то при всех значениях Da будет существовать единственное решение. Для реакции первого порядка это будет иметь место в случае, когда

YP<4(l-fP), (4.1.34)

для реакции произвольного положительного порядка (п > 0) при условии

Т{у) = {п-1)у' + уЦ + у+1 -л)-i/Y(2+ P) + Y(1 + P)>0.

(4.1.35)

Рассмотрим теперь условия существования нескольких стационарных решений. Если критерий однозначности (4.1.35) выполняется не для всех значений числа Da, то функция F{y) при г/е(1; 1 4-Р) имеет локальный минимум и максимум (см.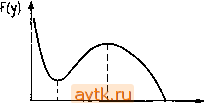

Ушш Углах У

Рис. 4.2. Минимум и максимум функции F{y].

рис. 4.2). Таким образом, существуют три стационарных состояния для значений числа Дамкёлера в диапазоне

(4.1.36)

(4.1.37)

Р - Da

Например, для реакции первого порядка оказывается y(2+P)±V(yP [уР-4(1-ьР)])

Утах, min - 2 (1 -- Р)

Анализу возможности существования нескольких стационарных состояний и примерам их возникновения в задачах теории горения и в моделях реакторов разных типов посвящена обширная литература [4.12-4.21].

4.2. ЗАДАЧИ С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ

В этом параграфе мы рассмотрим ряд физических проблем, анализ которых приводит к необходимости исследования систем обыкновенных дифференциальных уравнений. Эти проблемы будут представлены в форме, удобной для иллюстрации численных методов исследования нелинейных систем в гл. 5.

Системы дифференциальных уравнений мы будем записывать в виде

- = f(x, р), (4.2.1)

где хе R , х = (л:1, Хп)-вектор переменных состояния а в вектор р е R* включены параметры системы. При этом решение системы (4.2.1) определяется заданием начальных условий

х(0) = х . (4.2.2)

4.2.1. Задача 1. Реактор проточного типа с полным перемешиванием в случае неизотермической реакции и рецикла

Рассматриваемый реактор схематически представлен на рис. 4.3. Будем предполагать, что реакционная смесь полностью перемешивается и что объем реактора V, объемный расход Fo, входная концентрация Сдо и температура на входе Го, а также

Рис. 4.3. Реактор проточного типа с перемешиванием и рециклом.

коэффициент теплопередачи U, площадь поверхности теплообмена S, теплоемкость на единицу объема Ср и теплота реакции (-АЯг) остаются постоянными. Кроме того, мы будем предполагать, что температура охлаждающей среды не изменяется и что в реакторе происходит практически необратимая реакция типа А-> продукты.

С учетом этих предположений уравнения баланса массы н энтальпии можно представить в виде

dc д

l- = F[CAv~ca]-r(ca, Г)У, (Р1-1)

YCp = FCp{T.,-T\ + r{c; T){-AHr)V-US{T-T,). (Pl-2)

Положим л = Fq/F. Тогда

rv = Aro + (l-Л)Г, (Р1-3)

Cav = Acao + (1-Л)са. (Р1-4)

При этом реактор без рецикла соответствует случаю Л = 1.

X =-,

температуру число Дамкёлера

параметр тепловыделения

(-А^г)ао Е

энергию активации

v = W.,

температуру хладагента

параметр теплоотвода безразмерное время

t = tF/V.

Тогда уравнения баланса массы и энтальпии переписываются в виде

= - Лх -f Da (1 - X) ехр {ттщ)

= - Лв -f Da S (1 - X) ехр (jq) - P (© - в,.). (Pl-7)

Уравнения (Pl-6), (Pl-7) могут быть представлены в форме (4.2.1), где

х = (х, 0),

р = (Л, Da, Y, В, р, 0,). Обозначим через т время задержки : т = V/F. Тогда

Da = V. Р=ат, где a = US/VCp. (Р1-8)

Рассмотрим реакцию 1-го порядка, для которой r = kcA = йсоСд ехр i-E/RT).

Определим следующие безразмерные величины: конверсию

4.2.2. Задача 2. Каскад из двух неизотермических

проточных реакторов с полным перемешиванием и рециклом

Система из двух реакторов схематически представлена на рис. 4.4. Используя те же предположения, что в задаче I, урав-

Tq 1 Сдо Ту , Од.

Tj.c

Рис. 4.4. Два реактора проточного типа с перемешиванием и рециклом.

нения баланса массы и энтальпии в этом случае можно записать в виде

(Р2-1)

{Р2-2) (Р2-3)

У г = -Р [са1 - са2] - г (са2, Гг) Fj.

= f С, [Г1 - Гг] + г (СА2, Гг) (- АЯг) Уг - г^г (П - Г,г).

(Р2-4)

Введем следующие безразмерные величины: для /=1, 2 положим

, 6, = -(Г,-Го), р,= о

(Р2-5а)

и, кроме того, примем

Е

ао

У

, Dai = &o-, Da2 = &o-/, (P2-5b)

CAv = (1 - a) CA2 + Acao.

Формулами (Р2-10) время задержки т(= VjF) определено для одинаковых реакторов. - Прим. ред.

7 М. Холодннок н др.

Введенные здесь переменные и параметры соответствуют безразмерным величинам, определенным в задаче 1. Аналогичным образом мы поступили бы и в случае каскада, состоящего из большего числа реакторов (для некоторых процессов полимеризации используются каскады, состоящие из 10-12 ступеней).

Воспользовавшись формулами (Р2-5), преобразуем уравнения (Р2-1) - (Р2-4) к безразмерному виду (здесь мы вновь рассматриваем реакцию первого порядка)

= (1 - Л) Х2 - X, -f Da, (1 - X,) ехр [j) . (Р2-6)

= (l-A)02-e, + Da,B(l-,)exp (, J-Р.Св.-в ),

(Р2-7)

= - -2 + (1 - х^) ехр [j) , (Р2-8)

x = 0, - 02 -f Da2B (1 - Х2) ехр ( , Д) - Р2 (вг - 6,2).

(Р2-9)

Так же, как в задаче 1, можно ввести параметр т, характеризующий время задержки, полагая

Da, = Da2 = V, Pi = P2 = at- (Р2-10)

Уравнения (Р2-6) - (Р2-9) можно представить в форме (4.2.1), положив х = (х„ 0 Х2, 02), р = (А, Da Da2, Р Рг, 0ci, 02 Y, Р).

4.2.3. Задача 3. Проточный реактор с полным перемешиванием и с автокаталитической системой реакций (модель Нойеса - Филда)

Реакция Белоусова - Жаботинского представляет собой процесс окисления малоновой или броммалоновой кислоты ионами броматов в кислой среде, катализированный ионами переходных металлов (церия, железа). При различных условиях в реакторе проточного типа с перемешиванием можно наблюдать длительные автоколебания, несколько стационарных состояний в периодических режимов, хаотическое поведение, а в распределенных системах - распространяющиеся концентрационные волны окисления и восстановления [4.24, 4.25]. Указанная

r = 2ksCACX - kCBCz

dcz dt

(здесь С/ означает концентрацию компоненты /). Введем новые переменные

д; = сосх, y = t]CY, z = ycz, t = bt. Тогда кинетические уравнения (РЗ-2) примут вид

t-T(*. i-*=+* .v-2*.5-).

l-i(2*.-T-*= f)

реакция служит моделью при исследовании нелинейных явлений в химической кинетике. Филд, Кёрёш и Нойес [4.26] разработали подробную схему механизма этой реакции, состоящую из одиннадцати основных реакций между двенадцатью компонентами. Позднее Филд и Нойес [4.27] предложили упрощенную схему, состоящую из пяти основных этапов. Обозначим компоненты реакции следующим образом: А==ВгОз, В = ВгМА, Р = НОВг, Х = НВг02, Y = Br, Z = C& и запишем эту реакцию в виде следующей схемы:

Константа скорости реакции

(l)A-fYX-fP

(2) X-f Y->2P k

(3) A-f X->2X-f 2Z k (P3-1) (4)2XA-fP &4

(5) B-f Z/iY h

Предположим, что компоненты A и В находятся в большом избытке и что их концентрации не зависят от времени. Тогда изменение во времени концентраций остальных компонентов в замкнутой системе можно описать с помощью уравнений

-jp- - kCCi - kCyC, -4- зСдСх - 2kc\,

7г = - kiCp,c\ - hcxc\ + hkCBCz, (P3-2)

2kik

2k. k k.k.c

= S = 2h, (P3-4)

з^а з'а (з'а)

Уравнения (РЗ-3) при этом переписываются в следующем безразмерном виде:

= liy - xy + x - x.

B=-liy-xy + gz, (РЗ-5)

§=х-г.

Уравнения (РЗ-5) описывают процесс реакции в реакторе с полностью загруженной активной зоной (т. е. без подачи и отвода соответствующих компонент).

Таким образом, скорости образования отдельных компонент можно записать как

Гх = {\1у - ху + х - х-)/е,

г у = (- ,иг/ -ху + gz)/e, (РЗ-6)

Гг = Х - г.

Тогда уравнения баланса компонент X, Y, Z в реакторе проточного типа с перемешиванием для случая установившегося режима принимают вид {хо, г/о, Zo - соответствующие концентрации на входе)

F{Xo-x) + Vr = 0,

F{yo-y) + Vr = 0, (РЗ-7)

F{Zo-z) + Vr = 0.

Компоненты реакции X (НВГО2) и Z (Се+) представляют собой промежуточные продукты, возникающие в ходе реакции. При этом в реактор проточного типа с перемешиванием подается только компонента Y (Вг-).

Если хо = 20 = О, то, полагая F/V=, уо = а и вводя затем обозначения х = Х\, у = Х2 и г = хз, уравнения (РЗ-7)

Выберем теперь со, г\, у, б так, чтобы полученные уравнения имели максимально простой вид. Положим

С учетом формул (РЗ-6) можно переписать в виде [цх - х^х^ + Jf, - Jf?)/e - Рл:, = О,

(-р,Х2 - + gxif! + Р (а - 2) = О,

л:, - лгз-рл:з = 0. (РЗ-8)

Таким образом, для уравнения в форме (4.2.1) в данном случае мы имеем х= {х\, хг, Хз), р= (ц, е, б', р, g, а).

Более подробно кинетические модели реакции Белоусова- Жаботинского обсуждаются в работах [4.28, 4.29].

4.2.4. Задача 4. SH-модель метаболизма тиолов

Химические процессы, происходящие при окислении низкомолекулярных тиолов (глютатион, цистеин и т. д.) в клеточных белках, могут быть описаны схемой реакций, представленной на рис. 4.5.

Синтез воссгланоЗ/1Енных тио/1ов

гротеинов

Использодате и деградация

-Sh-

S Р, -S

S p-S

Восстонодлечие протеинов--*SS

SH -SH

Окисленные протеины

BoccmoHoS/ieHHbie протеины

и другие Продукты

и другие перекиси

субстраты для окисления

Рис. 4.5. Упрощенная схема реакций метаболизма тиолов

Для изменения во времени концентраций S -Н и S -S групп в низкомолекулярных тиолах при использовании ряда упрощающих предположений можно получить следующую модель [4.30-4.32]:

= а (v -f Г)/(1-f Х^) - Z (1-f У), = Х(р + У)-бУ.

(Р4-1) (Р4-2)