О 0,5 Z

Рис. 5.30. Составляющая Xi (2) периодической траектории задачи 8, N = 2, в точке бифуркации типа -1 . Параметры взяты из табл. 5.25. Первая точка из этой таблицы выбрана в качестве начальной точки траектории. Нумерация тех точек, где X\{z)= 2, используется в табл. 5.26.

тем, что в окрестности выбранных значений параметров существует много точек бифуркации (более подробные результаты можно найти в работе [5.26]).

Таблица 5.25. Точки бифуркации удвоения периода для задачи 8 (рис. 5.27а): Л = 2, В = 5,9, р = DJDi = 0,1, = 1, Tift = 2.

Можно разработать аналогичные методы для нахождения точек бифуркации -f 1 и бифуркации рождения тора. Так, в случае бифуркации -+-1 (в автономной системе дифференци-

В табл. 5.27 показан ход итераций по схеме Ньютона в случае метода 1. Метод сходится к первой точке из табл. 5.25, а более точно - к четвертому решению из табл. 5.26. При проведении расчетов оказалось, что области начальных приближений, для которых метод Ньютона сходился к выбранным точкам бифуркации -1 , относительно невелики. Это объясняется

Таблица 5.26. Четыре различных решения, соответствующие первой точке в табл. 5.25 (см. рис. 5.30): Т = 11,59421, а = 1,22382

Таблица 5.27. Вычисление точки бифуркации удвоения периода для задачи 8. Пример итераций в случае метода 1: А - 2, В = 5,9, р = Z)i/£)2 = 0,1, k = I, r\k = 2. Начальное приближение для метода Ньютона выбиралось случайным образом.

альных уравнений) характеристическое уравнение (5.8.28) имеет двукратный корень +1. т. е. должно выполняться соотношение

Pn+i(r\i.....Ла+ь л а) = -(1) = 0 (5.8.32)

(условие Р(1) = 0 выполняется автоматически). Уравнения (5.8.19) и (5.8.32) вновь представляют собой систему n+l нелинейных (алгебраических) уравнений относительно п~\- 1 неизвестных 111, ..., r\k-i, Цк+и ..,г\п,Т, а (переменную щ мы опять считаем фиксированной). Далее действуем точно так же, как в методе 1 для точек бифуркации типа -Ь.

В случае бифуркации типа тора указанный подход несколько усложняется. Эта бифуркация (см. гл. 2) характеризуется наличием пары комплексно сопряженных собственных чисел Яг, з матрицы монодромии, которые переходят через единичную окружность и для которых в точке бифуркации выполняются соотношения

1Чз1=1. КТ.зФ1, m=I, 2. 3, 4.

(5.8.33)

Будем искать периодические решения, у которых два мультипликатора имеют вид

Оба последующих метода основаны на использовании подходящего разложения характеристического многочлена.

Метод 3 (бифуркация типа тора) Выделив из Р {К) множитель - (о^+ 1, напишем

Р (К) = {к - (оЯ + 1) + fti- + ... + 6 2) + CK + D.

(5.8.34)

Здесь (о = 2а и Х^ - ак-\-\={к - Х2){Х - Хз). Коэффициенты bi, b -2. С, D находятся с помощью рекуррентных формул (6о= 1,6-1=0):

6 = + со6 , - 6 2, m = 1, 2, ..., п - 2, (5.8.35) С = а„ 1 + (о6 2 - 6 з, Z) = а„ - (5.8.36)

При этом в точке бифуркации типа тора имеют место соотношения

...,Щ-и Щ+и а, (о) = С = 0, (5.8.37а)

+2К.....Лй-1. Пк+и ..., Л , а, сй) = О = 0. (5.8.37Ь)

Уравнения (5.8.19) и (5.8.37) представляют собой систему п+2 нелинейных (алгебраических) уравнений относительно п + 2 неизвестных Til, ..., Цк-х, Цк+и Цп, Т, а, (О (неизвестная снова считается фиксированной).

Метод 4 (бифуркация типа тора)

При разложении характеристического многочлена Р{Х) можно использовать то обстоятельство, что (в автономном случае) всегда есть корень i = 1. Разложение при этом принимает вид

Р(Я) = (ЯЗ-(2а+ 1)Л,2 + (2а+ 1)Х-1)Х X {X~ + ЬХ~ + ... + 6 -з) + сх + DX + E. (5.8.38)

(5.8.39)

Коэффициенты 6ь Ьп-з, С, D, Е вновь подсчитываются по рекуррентным формулам {Ьо=1, b-i = Q, 6 2 = 0; (о = 2а)

ftm = am + (a+ 1)(&т-1 -т-2) + т-3. =1, 2, . . ., П - 3, с = а„ 2 + b s + (со + 1) {Ьгг-3 - Ьп-),

D = а„ , + 6 4 - (со + 1) 6 з, £ = а„ + & -з.

Если коэффициенты С и О в соотношениях (5.8.37) вычислить по формулам (5.8.39), то уравнения (5.8.19) и (5.8.37) будут представлять собой систему -(-2 нелинейных уравнений относительно п--2 неизвестных, как и в методе 3 (в найденной точке бифуркации типа тора условие £ = О выполняется автоматически). Вместо соотношений (5.8.37) мы могли бы взять условия С = £ = 0 или £) = £ = О (поскольку Р(1) = 0, то С + + О + £ = О, см. (5.8.38)). Для решения получаемых систем нелинейных уравнений можно вновь воспользоваться методом Ньютона. Можно поступить и так: с помощью метода Гаусса - Ньютона решить систему п + З уравнений (5.8.19), (5.8.37) и £ = О относительно и + 2 неизвестных.

В табл. 5.28 приведены точки бифуркации типа тора для задачи 8, найденные описанными выше методами. Отметим, что метод Ньютона является очень чувствительным к выбору начального приближения. При этом подходящее начальное приближение находится обычно с помощью продолжения соответствующей ветви периодических решений. В табл. 5.29 указана одна точка бифуркации типа тора из табл. 5.28 в четырех различных представлениях. Эти различные представления отвечают наличию на траектории периодического решения нескольких точек, в которых Xk(z) принимает заданное значение. Для точки бифуркации при В - 5,5 из табл. 5.28 график функции Xi{z) пересекает прямую tii==2 четыре раза. В табл. 5.29 приведены только значения координат TI2, Лз и (значения Т и а, конечно, одинаковы для всех представлений).

Таблица 5.28. Точки бифуркации типа тора для задачи 8 (А = 2, р = D,/D2 = 0,1, k= \,щ = 2).

На рис. 5.31 представлена бифуркационная диаграмма для точек бифуркации типа тора в плоскости параметров В - Z)i. Точки, в которых Х^=1 или V=l, обозначены как 37 и 47

0.05 o<.= D,

Рис. 5.31. Бифуркационная диаграмма периодических решений. Бифуркация типа тора. Задача 8, А = 2, р = О^/Оз = 0,1.

соответственно. Изображенная на рисунке кривая заканчивается в обозначенных кружком точках, для которых 1=,2 = = 3 = 1.

В заключение данного пункта отметим, что описанные выше методы можно без затруднений использовать для вычисления точек бифуркации и в случае неавтономных систем обыкновенных дифференциальных уравнений (см. § 5.11). Кроме того, на основе результатов п. 5.4.2 в точке бифуркации типа -1 можно определить направление ветви решений с двойным периодом.

Таблица 5.29. Точка бифуркации типа тора в четырех представлениях; задача 8 (Л = 2, В = 5,5, р = Dj/Da = 0,1, = 1, r\k = 2); Г = 8,32408, а = Di == 0,052495, со = -1,08277.

5.8.6. Метод многократнай стрельбы

Метод стрельбы, называемый также иногда методом простой стрельбы (см. п. 5.8.2), в случае сильно неустойчивых периодических решений практически ие работает. В таких случаях можно использовать коиечио-разностный метод, который, однако, не дает нам информации об устойчивости найденного периодического решения; кроме того, размерность решаемых задач оказывается достаточно высокой. Определенным компромиссом между методом стрельбы и разностным методом является метод многократной стрельбы. Он позволяет ие только находить сильно неустойчивые периодические решения, но и достаточно просто получать информацию об их устойчивости.

Приступая к описанию метода, разобьем интервал [О, 1] иа т - 1 подынтервалов с помощью точек zy:

О = Zi < z, < ... < z i < z = 1, AZj = Zj+i - Zj, /=1, 2, m-1.

В точках Zj, j = 1,2, m - 1, выберем начальные условия вида

х(2/) = 11/==(Лл. V). (5.8.40)

Кроме того, зададимся определенным значением периода Т. Интегрируя уравнения (5.8.4) иа интервалах [zy, z/+i] с начальными условиями (5.8.40), можно найти решение в точке z/+i; обозначим его как x(z/+i 7 , а). Для того чтобы решение в точке Z/+1 было непрерывным, потребуем выполнения условий

Fjx{Zj+i\nj, Т, а)-rij+i = 0, /=1,2.....m-1. (5.8.41)

Кроме того, из условий периодичности (5.8.5) следует, что г\\ = г\т. Уравнения (5.8.41) представляют собой систему п{т-1) нелинейных (алгебраических) уравнений относительно п{т - \)+1 неизвестных {r\i, г\2, Цт-и Т). Так же, как в случае простой стрельбы, одну составляющую вектора r\i, а именно tiis, зафиксируем. Обозначим tj, = (Ti j, tii, Ц1,к+1, Цхп). Тогда уравнения (5.8.41) можно рассматривать как систему п{т - 1) нелинейных уравнений относительно

n{in-1) неизвестных (Ль Лг 4m-i> ) и одного параметра а.

Для продолжения решения уравнений (5.8.41) в зависимости от параметра а можно вновь воспользоваться алгоритмом DERPER, который был описай в п. 5.8.4. Матрица Якоби

О G, 2 -/ ......

.-10 О G , aF ,/ar dF Jda

Здесь Gf- матрицы размера пХп,

(5.8.42)

дх,.(г.., IT) Г, а)-

1 ; ; 1 единичная матрица;

-, /, р=1,...,/г, / -(

(5.8.43)

матрица Gj получается из матрицы Gj вычеркиванием й-го столбца; аналогично из / получается 7.

Частные производные можно найти, используя уравнения в вариациях

= Т °) и, (5.8.44)

где [/ - матрица размера пХ - Если выбрать начальное условие в виде U{Zf) = I, то, интегрируя уравнения (5.8.44) иа интервале [zj,Zj+i], мы получим Gj = U(Zj+i). Для частных производных dFj/df имеют место соотношения

дР,/дТ = Az,-f (х {Zi+г) I Л/, Т, а). (5.8.45)

Частные производные dFj/da находятся интегрированием уравнений в вариациях, аналогичных уравнениям (5.8.44).

В п. 5.8.3 мы говорили о структуре матрицы монодромии в случае метода простой стрельбы. В методе многократной стрельбы матрица монодромии имеет вид

fi = G ,G 2 ... GGb (5.8.46)

где матрицы G / = 1, 2, т-1, определяются формулой (5.8.43). Отметим, что столь простую структуру матрицы монодромии невозможно получить при использовании разностных методов.

Метод многократной стрельбы был нами использован для нахождения сильно неустойчивых периодических решений в так называемой модели Ходжкина-Хаксли передачи возмущения по нервному волокну [5.20], а также для продолжения по параметру периодических решений задачи 8 [5.29].

системы (5.8.41) имеет вид

Gi -I О ... dFildT dfi/da

О Ог -/ ... dFJdT dFJda

Отметим в заключение, что в то время как при использовании разностного метода нам приходилось брать порядка ста точек деления, в случае применения метода многократной стрельбы число точек деления было существенно меньше. Практический опыт показывает [5.20], что уже десяти точек бывает вполне достаточно.

5.9. ХАОТИЧЕСКИЕ АТТРАКТОРЫ

Материал данного параграфа основывается на сведениях, изложенных в п. 2.5.2, где были введены понятия аттрактора и хаотического инвариантного множества.

Хаотическое инвариантное множество, представляющее собой аттрактор, называется хаотическим (странным) аттрактором.

Наличие хаотического аттрактора в фазовом пространстве системы дифференциальных уравнений служит причиной сложного поведения траекторий системы в его окрестности. При этом мы говорим о хаотическом поведении траектории (или решения данной системы). Пример такого поведения изображен на рис. 5.32.

О существовании сложных траекторий в автономных системах обыкновенных дифференциальных уравнений с размерностью, больше или равной трем, было известно еще Пуанкаре. Лоренц в работе [4.40] на простом численном примере [задача 10 при значениях параметров а =10, ft = 8/3, /- = 28) продемонстрировал наличие хаотического поведения решений.

Один из механизмов возникновения хаотического множества связан с последовательностью бифуркаций удвоения периода (или бифуркаций типа -1 , см. § 5.8, 2.3 и 2.5). Этой последовательности бифуркаций часто соответствует сходящаяся последовательность {а„} бифуркационных значений параметра а. Положим lima = a. В случае если а„ / (или соот-

П-*<х>

ветственно а„\.аоо) при а > а, (соответственно а < осо) в фазовом пространстве системы x = f(x, а) существует хаотическое множество (см. рис. 5.34f).

Ниже мы рассмотрим некоторые методы анализа хаотических аттракторов. Для описания хаотического аттрактора мы будем использовать показатели Ляпунова (см. § 2.5) или будем изучать его структуру с помощью отображения Пуанкаре. Хаотический аттрактор характеризуется наличием хотя бы одного положительного одномерного показателя Ляпунова или тем, что инвариантное множество соответствующего отображе-

ния Пуанкаре имеет характер канторова множестваБолее подробно вопросы возникновения и анализа хаотического пове-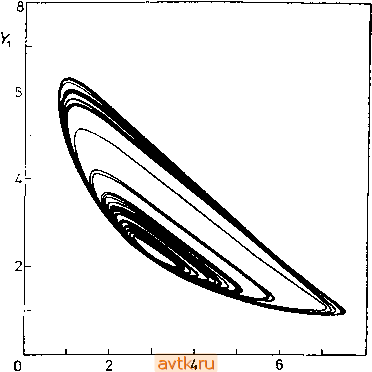

Al 8

Рис. 5.32. Фазовый портрет задачи 8, N=2, Л i= 2, fi = 5,9, Dj = 1,21, D2= 12,1. Часть хаотической траектории в проекции на плоскость Xi-Y.

дения систем с соответствующими приложениями рассматриваются в работе [5.18].

5.9.1. Вычисление показателей Ляпунова

Рассмотрим систему п дифференциальных уравнений

= f(x, а), (хе R ), aRK

(5.9.1)

> Понимание смысла последнего высказывания для дальнейшего не обязательно. - Ярмж. ред.

Я1(х„; v?)= to-ln-. (5.9.2)

Соответствующий й-мерный показатель задается соотношением

(5.9.3)

Я*(х„; v°. ....v°)= limi-ln

Здесь wiAw2 ... Awsll есть объем -мерного параллелепипеда, образуемого векторами Wi, ..., w*. В формулах (5.9.2) и (5.9.3) есть решение линеаризованного уравнения

= --(ф(0)У. (5.9.4)

для которого уДО) = у? (матрица di/dx вычисляется в точках выбранной траектории x = ф(/) системы (5.9.1)). Замечания

1. Предел в формуле (5.9.2) существует для почти всех хо и векторов Vi.

2. При случайном выборе линейно независимых векторов Vp v° формула (5.9.3) с вероятностью 1 дает максимальный -мерный показатель Я^ (см. теорему в п. 2.5.1)

Вычисление одномерных показателей Ляпунова обычно проводится следующим образом. С помощью формулы (5.9.3) подсчитываем П максимальных показателей Я|пах, Ятах, Ятах

и затем находим одномерные показатели Я'Я' ... Я^ с помощью соотношений

я! = Ятах, Яй = Ятах - Ят1х , k = 2,...,n, (5.9.5)

поскольку каждый -мерный показатель представляет собой сумму k одномерных показателей (см. п. 2.5.1).

Если подсчитывать показатели Ляпунова с помощью выражения (5.9.3), то у нас могут возникнуть трудности вычислительного порядка. Так, например, если точка Xq лежит на хаотической траектории, то с ростом t векторы увеличиваются, а углы между ними уменьшаются, в результате чего вычисление

> Для придания точного смысла этим утверждениям нужно расшифровать термины почти все и с вероятностью I . - Прим. ред.

В П. 2.5.1 МЫ ввели определение показателей Ляпунова. Напомним, что для траектории системы (5.9.1), которая в момент /=0 проходит через точку Хо (при фиксированном значении а), одномерный показатель Я' определяется как

1 J\