Если принять максимально допустимую погрешность аппроксимации равной е, то мы можем выбрать решение Qi, если < е, или решение Q2, если Е2 < е. Если же не выполнено ни одно из этих условий, то нам придется повторить вычисления для меньшего значения шага /13, выбираемого в соответствии с оценкой

/tз^/t,(-;-) (5.7.14)

Всю схему вычислений можно повторить еще раз, либо с определенной долей риска остановиться на решении Q3, найденном с шагом Аз. В общем случае проблема анализа погрешностей аппроксимации оказывается гораздо более сложной, поэтому читателя, который глубже заинтересуется указанной проблемой, мы отсылаем к оригинальной литературе.

5.7.1.4. Автоматическое изменение uiaea h

Очень часто случается, что решение х() в разных областях изменения независимой переменной t обладает различными свойствами и, следовательно, для того чтобы выдержать предписанную точность, в каждой из этих областей нужно было бы использовать выбранный метод численного интегрирования с длиной шага, зависящей от области. Наиболее простой путь заключается в том, чтобы для всего промежутка интегрирования выбрать некую минимальную величину шага (найдя ее с помощью апостериорной оценки погрешности аппроксимации на всем рассматриваемом промежутке). Однако в большинстве областей интегрирование будет проводиться с излишней точностью и, следовательно, окажется неэкономичным. Одношаговые методы (см. (5.7.2)) позволяют нужным образом изменять величину шага интегрирования в зависимости от свойств решения. Простой алгоритм автоматического изменения шага можно получить на основе апостериорной оценки погрешности аппроксимации, вычисленной на каждом шаге интегрирования, однако такой путь неэффективен. Впервые эффективная схема вычислений с автоматическим изменением шага была разработана Мерсоном (см. табл. 5.18). В случае метода четвертого порядка нам требуется проводить пять вычислений правых частей дифференциальных уравнений, т. е. на одно больше, чем в случае стандартного метода четвертого порядка. Этот избыток информации используется для оценки погрешности на данном шаге:

Е' = II (2ki - 9кз + 8к4 - к5)/3011. (5.7.15)

Пусть е' - максимальная допустимая погрешность на одном шаге. Если Е' < е', то полученный результат считается

Предположение, что суммарная погрешность округления пропорциональна числу шагов, не очень реалистично. - Прим. ред.

приемлемым, если же Е' > е', то результат считается неприемлемым (и алгоритм не увеличивает t). В обоих случаях шаг для дальнейшего, интегрирования подсчитывается по формуле

А -ь.й == (o/i P ()°. (5.7.16)

которая соответствует оценке (5.7.14) при р - 5 ( = 1--порядок метода). Значение параметра безопасности и выбирается между 0,8 и 0,9. Тем самым мы предупреждаем ситуации, при которых выбор шага h = /1 °вый jjg обеспечивает предписанную заранее точность. Фактическая погрешность на всем промежутке интегрирования тесно связана с величиной е в тех случаях, когда дифференциальное уравнение не слишком увеличивает величину соответствующих погрешностей, т. е. когда погрешность на М шагах приближенно равняется М-кратной погрешности, полученной на одном шаге.

Целую группу методов, аналогичных методу Мерсона, разработал в последнее время Фелберг. При этом правые части системы приходится вычислять большее число раз, чем минимально необходимо для схемы данного порядка.

5.7.1.5. Погрешности аппроксимации и погрешности округления

В рассматривавшихся до сих пор задачах мы пренебрегали погрешностями округления; при этом неявно предполагалось, что по порядку они меньше, чем погрешности аппроксимации. Это предположение несправедливо в случае повышенных требований к точности решения, т. е. при очень малых значениях шага h. Рассмотрим теперь схематически зависимости этих погрешностей от величины шага h. Если мы выбираем в качестве некоторой характерной величины погрешностей округления погрешности, возникаюшие при вычислениях на одном шаге метода интегрирования, а число шагов (при фиксированном t) равно t/h, то суммарная погрешность округления оказывается пропорциональной Л .В то же время зависимость погрешности аппроксимации от шага h определяется формулой (5.7.9). На рис. 5.21а графически изображен случай р = 1 (метод Эйлера). Из рисунка видно, что существует нижняя граница итоговой погрешности Е*, меньше которой нельзя получить с помощью выбора шага h. Если мы хотим получить решение с более высокой точностью, чем Е*, то нам нужно либо повысить порядок метода

(см. рис. 5.2lb), либо уменьшить погрешности округления (перейти к вычислениям с двойной точностью).

Замечание. На рис. 5.21 схематически показано поведение погрешностей при к-О. В практических расчетах обычно ис-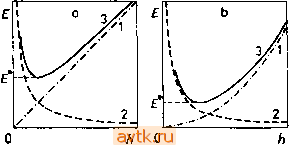

Рис. 5.21. Зависимость погрешности аппроксимации (1), погрешности округления (2) и полной погрешности (3) от шага А. а) р = I, Ь) р = 2.

пользуются достаточно большие h - такие, чтобы можно было пренебречь погрешностями округления.

5.7.2. Многошаговые методы

Многошаговые методы в отличие от одношаговых используют значения решения и правых частей не в одной, а в нескольких предшествующих узловых точках. Линейный -шаго-вый метод в случае постоянного шага h описывается соотношением

= h [W + Pft-if + ... + Pofl, (5.7.17)

где а^ф О, al + 1>0 и использовано обозначение i = i{ts, X*). Существует целый ряд различных многошаговых методов. В частном случае = 1, a-i = -1, аг = 0 при 4 = 0, 1, k - 2 соотношение (5.7.17) называется методом Адамса. При = О эти методы называются явными, поскольку (при известных х', х'-*+) мы можем найти х'+ из формулы (5.7.17) неитерационным способом. Такой вариант метода Адамса называют методом Адамса - Бэшфорта; его коэффициенты приведены в табл. 5.19. В случае кфЬ методы, описываемые соотношением (5.7.17), оказываются неявными, поскольку х'+ входит и в правую часть формулы (5.7.17). Неявный вариант метода Адамса называют методом Адамса - Моултона, а его

Таблица 5.19. Коэффициенты метода Адамса - Бэшфорта в случае погрешности аппроксимации р-го поридка

Таблица 5.20. Коэффициенты метода Адамса - Моултоиа в случае погрешности аппроксимации р-го порядка

* Особый случав X

.l+K

=jc-(-Af(неявный метод Эйлера).

коэффициенты представлены в табл. 5.20. При этом для нахождения х'+ (по известным х', x-*+i) мы должны уже использовать какую-нибудь итерационную процедуру, для которой мы располагаем достаточно хорошим начальным приближением X, это начальное приближение может определяться с помощью какого-либо явного метода. Так возникает метод типа предиктор - корректор.

Многошаговые методы по сравнению с одношаговыми обладают более высокой эффективностью, заключающейся в необходимости проведения меньшего количества вычислений правых частей за один шаг интегрирования при одном и том же порядке метода. С другой стороны, для их запуска приходится использовать какую-либо иную вычислительную схему (например, одношаговый метод), поскольку самих по себе начальных условий недостаточно для начала расчета. Другим недостатком этих методов является трудность реализации алгоритма в случае автоматического изменения шага интегрирова-

ния. Такого рода алгоритм, основанный на методах Адамса - Бэшфорта - Моултона и подробно разработанный Гиром, очень часто используется в приложениях.

5.7.3. Методы интегрирования жестких систем

Если вещественные части собственных чисел матрицы Якоби для правых частей дифференциальных уравнений (5.7.1) различаются на несколько порядков, то такие системы обычно называют жесткими. Они описывают результат наложения нескольких различных процессов, скорости которых существенно различаются между собой (в частности, быстрых и медленных реакций). Указанное понятие возникло в связи с численным решением дифференциальных уравнений.

Рассмотрим простой пример. Пусть нам нужно решить дифференциальное уравнение

jc = 1000jc, jc(0)=l (5.7.18)

методом Эйлера. Точное решение этой задачи имеет вид x(t) = - g-iooot и, следовательно, при />0,01 оно практически равно нулю. Методом Эйлера (5.7.8) находим

jc/+i = (l- 1000/i)jc xP=l, (5.7.19)

и, следовательно,

х' = {1- moh).

Легко видеть, что при А > 0,002 получим х'-оо при j-oo, и значит, для аппроксимации практически постоянной (равной нулю) функции нам нужно использовать чрезвычайно малый шаг. В случае жестких систем подобными свойствами обладают все явные методы интегрирования, так что их применение весьма неэффективно. При этом оказывается, что с практической точки зрения для интегрирования жестких систем удобны лишь так называемые А-устойчивые методы. Относительно Л-устойчивости данного метода можно просто судить по его поведению при решении скалярного дифференциального уравнения

==Хх, (5.7.20)

где X - в общем случае комплексное число с отрицательной вещественной частью. Численная схема, с помощью которой строится последовательность значений х' при постоянном шаге интегрирования h, называется Л-устойчивой, если в рекуррентной формуле

xf+ = P{hX)x (5.7.21)

множитель Р удовлетворяет соотношению

\рт\<1

(5.7.22)

при произвольном л > 0. Это определение по существу представляет собой требование, чтобы х'- -0 при произвольном Л > 0. Указанное требование можно усилить; например, для Ь-устойчивой схемы необходимо потребовать, чтобы \P{hX)\-*-- -0 при h-oo.

За последние 15 лет был разработан целый ряд численных методов для решения жестких систем дифференциальных уравнений. Эти методы можно ориентировочно разделить на три группы. К первой относится модифицированный алгоритм Гира, основанный на многошаговой схеме типа предиктор - корректор. Этот метод используется очень широко и включается в стандартное программное обеспечение многих ЭВМ. Ко второй группе относятся так называемые полунеявные варианты метода Рунге - Кутты. В случае автономной системы

= f(x)

(5.7.23)

одна такая группа методов описывается соотношениями (ср. формулы (5.7.5), (5.7.6))

k, = /i;[I-ViJ(xrf(x).

кг = hi [I - hioi (x -f c,k,)]- f (x -f 6,k,), (5.7.24) x/+i==x-f Y,k,-f Yaka,

где через J = -f обозначена матрица Якоби.

Коэффициенты а\, а% Ь\, Сь yi и уг приведены в табл. 5.21.

Таблица 5.21. Коэффициенты полунеявных вариантов метода Рунге - Кутты (5.7.24)

Все эти методы Л-устойчивы, в чем можно убедиться непосредственной подстановкой в уравнение (5.7.20). В этих методах не нужно прибегать к итерационным процедурам, но необходимо вычислять матрицу Якоби J. Кроме того, на каждом шаге приходится дважды решать систему линейных алгебраических уравнений относительно неизвестных ki и кг.

К третьей группе принадлежат методы, в которых используются вторые производные решения. Одним из таких методов является схема Линнигера - Уиллоуби (см. [5.31]).

5.7.4. Системы дифференциальных и алгебраических уравнений

Довольно часто встречаются системы, включающие как дифференциальные, так и алгебраические уравнения (термин алгебраический используется здесь для обозначения уравнения, не являющегося дифференциальным); возьмем, скажем, систему

f-Ht, X, U), (5.7.25)

0 = g( X, u), (5.7.26)

где X е R , f е R , u е R *, g e R *. Системы такого типа возникают, к примеру, в моделях, описывающих химическую кинетику.

Для решения системы (5.7.25), (5.7.26) могут быть использованы два подхода. Первый из них состоит в интегрировании уравнений (5.7.25) с помощью какого-либо общеупотребительного метода, причем при каждом вычислении правых частей f решается система т нелинейных уравнений (5.7.26) относительно неизвестной и. Начальная оценка и для используемой итерационной процедуры получается из предыдущего этапа вычислений правой части. Для начального условия

/ = 0: х(0) = х , u(0) = u<, (5.7.27)

естественно, должно иметь место соотношение

g(0, X , u) = 0. (5.7.28)

Второй подход заключается в преобразовании системы алгебраических уравнений в систему дифференциальных уравнений. С этой целью продифференцируем уравнения (5.7.26) по переменной , и в результате мы получим систему

4£4l Lf 4L. (5.7.29)

да dt дх dt

Для системы п-\-т дифференциальных уравнений (5.7.25), (5.7.29) мы имеем начальные условия (5.7.27).

При этом мы предполагали, что матрица dg/du является регулярной вдоль соответствующей траектории. Если же она не регулярна, то возникают трудности в обоих подходах: непрерывное решение vi{t) системы (5.7.26) может не существовать (или быть неединственным). В таких случаях необходимо оценить полученные результаты с физической точки зрения, а также проанализировать обоснованность модели (5.7.25), (5.7.26). Рассмотренный выше случай-самый простой; более сложные случаи обсуждаются, например, в [5.34].

5.7.5. Интегрирование дифференциальных уравнений с запаздыванием

Дифференциальные уравнения с запаздыванием возникают при рассмотрении целого ряда математических моделей процессов переноса, теории автоматического регулирования, а также различного рода биологических объектов. Дифференцналь-йые уравнения с k различными запаздываниями Ti > О, ... ..., Tfe > О можно представить в виде

= f (, X(О, x{t-т,), ..., X(-т,)). (5.7.30)

Обозначим теперь т = шах т,-. Тогда для интегрирования уравнения (5.7.30) прн t > О нам потребуются начальные условия на промежутке t е [-т, 0]: мы должны знать

x(0 = q)(0, ti-c, 0]. (5.7.31)

Итак, в отличие от систем без запаздывания, для которых достаточно знать вектор начальных условий в один момент времени t, в данном случае для того, чтобы однозначно определить решение, мы должны его знать на целом промежутке изменения t. При этом изменение в методе интегрирования состоит лишь в том, что для вычисления правой части нужно использовать значения решения в точках t - n. Эти значения получаются с помощью интерполяции из таблицы значений (/, x(t)), систематически накапливаемых в ходе интегрирования. Такая таблица (память) заполняется сначала на основе знания начальных условий (5.7.31), а затем в процессе интегрирования постепенно обновляется (слишком старые значения изымаются из таблицы). Если мы используем метод интегрирования с автоматическим выбором шага, то указанная таблица оказывается неравномерной. А именно, в областях изменения /, где X меняется быстрее, таблица оказывается более плотной, это

= f(x, а) (5.8.1)

с одним параметром а (значение которого мы пока будем считать фиксированным). Периодическое решение х() системы (5.8.1), имеющее период Т, при любом /eR удовлетворяет условию

x{t-bT) = x(t). (5.8.2

Устойчивые периодические решения (т. е. притягивающие, или асимптотически орбитально устойчивые решения. - Ред.) (см. § 2.3) можно найти посредством процесса установления, имитируя (численно) динамику системы (5.8.1) с помощью методов, описанных в § 5.7 ~>. После установления колебаний нетрудно оценить (найти с помощью интерполяции) и величину периода Т. Неустойчивое периодическое решение этим способом найти нельзя, за исключением случаев, когда оно устойчиво при /->-оо (т. е. тогда, когда ни один мультипликатор не лежит внутри единичного круга, при п = 2 для неустойчивого периодического решения это всегда выполняется). Такие решения можно найти, интегрируя уравнение (5.8.1) в отрицательном направлении по оси времени.

Примером приложения указанного подхода служат периодические решения задачи 1, представленные в форме фазовых портретов на рис. 5.19. На рис. 5.22 изображены два вложенных один в другой предельных цикла. Внешний из них является устойчивым и был найден с помощью установления при /->-оо. Внутренний цикл неустойчив и был найден процессом установления в обращенном времени (при -оо).

Переходя к общему случаю, преобразуем независимую переменную t следующим образом;

t = Tz. (5.8.3)

1) Разумеется, для этого нужно знать точку, достаточно близкую к искомому решению. - Прим. ред.

обеспечивает сохранение точности в процессе интерполяции. Примером системы с временным запаздыванием служит задача 6, в которой функция роста задается формулой (Р6-4).

5.8. ВЫЧИСЛЕНИЕ ПЕРИОДИЧЕСКИХ РЕШЕНИЙ В АВТОНОМНОМ СЛУЧАЕ

Рассмотрим автономную систему п обыкновенных дифференциальных уравнений

Тогда соотношения (5.8.1) и (5.8.2) принимают вид

= ?f(x, а), (5.8.4)

х(1) = х(0), (5.8.5)

т. е. решение x{z) имеет период, равный единице (учитывая автономность системы, значение / в формуле (5.8.2) можно выбрать равным нулю).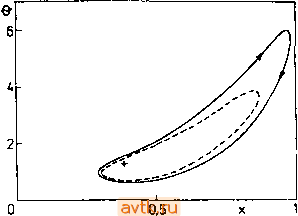

Рис. 5.22. Периодические решения задачи 1. Устойчивый (сплошная линия) и неустойчивый (штриховая линия) предельные циклы. Л = 1, В = 14, у-*-оо. Da = 0,1618, Р = 3, Gc = 0; -f устойчивое стационарное решение.

Соотношения (5.8.4), (5.8.5) определяют собой нелинейную краевую задачу со смешанными граничными условиями (более подробно нелинейные краевые задачи рассматриваются в § 6.1). Для решения такого рода задач чаще всего используются разностные методы и метод стрельбы.

5.8.1. Разностные методы

Идея разностных методов заключается в замене производных конечными разностями на достаточно густой сетке узловых точек Zi = ih, г = 0, 1, N, h= \/N. Простейшая такая замена дает вместо (5.8.4)

х'+-х' h

здесь X

= n(4-(x+-f х'), а), i = Q, \, N-\; (5.8.6)

x{Zi). Из граничных условий (5.8.5) имеем хО = х^.

(5.8.7)