объема становится все более неточным. Чтобы преодолеть эти затруднения, заметим, что отношение объемов v* (дробь, стоящая в формуле (5.9.3)) не изменится, если вместо векторов v°

взятьих (независимые) линейные комбинации wi, поскольку vjj зависит только от подпространства, натянутого на v9.

При вычислении показателей Ляпунова мы поступаем так. Задав небольшое т, вычисляем величину

v,(0; т)==

]у|л ... Avl

(5.9.6)

- коэффициент изменения -мерного объема за время 0

/т. Затем выбираем ортонормированный базис w,- (/ = = I, ..., k) в подпространстве, натянутом на у/, например, ортогонализируя v] по Граму-Шмидту. Затем на промежутке т^/2т вычисляем Гй(т;2т), используя решения w,(/) линеаризованного уравнения (5.9.4) с начальными данными w,(t) = w,-. Теперь коэффициент изменения объема за время 2т есть, очевидно, произведение: гй(0; 2т) = г*(0; т) г*(т; 2т). Проводя ортогонализацию и нормировку w,- в конце каждого интервала длины т, полагаем при t = Lr

Lx (L) = -Inv,(0; Lr).

(5.9.7)

В реальных вычислениях целое число L подбирается настолько большим, чтобы *(L-}-l) мало отличалось от *(L). Разумеется, для разных k могут понадобиться разные L.

Мы ограничимся здесь двумя примерами. На рис. 5.33 изображена зависимость максимального показателя Ляпунова V от параметра а для притягивающей траектории (в задаче 10). Учитывая большой объем необходимого машинного времени, вычисления проводились на относительно редкой сетке значений параметра г, выбранной на основе данных рис. 5.26. На рис. 5.33 можно видеть несколько интервалов изменения параметра (не-

Таблица 5.30. Одномерные показатели Ляпунова для задачи 8: N = 2, А=2, В = 5,9, D1/D2 = 0,1.

которые ИЗ них весьма малы), в которых существуют устойчивые периодические решения {К1 = 0{см. рис. 5.26). При этом на интервалах, где Я^ > О, аттрактор является хаотическим.

В табл. 5.30 приведены численные значения показателей Ляпунова для задачи о двух связанных реакторах [задача 8)

50 100 150 200 250 Збб 0 450 500

Рис. 5.33. Зависимость максимального одномерного показателя Ляпунова Ящах параметра г в задаче 10, а = 16, & = 4.

при трех значениях параметра Du Положительная величина Я{ указывает на существование хаотических траекторий; при этом Я' всегда равно нулю (см. замечание 2 в п. 2.5.1).

5.9.2. Отображение Пуанкаре

В п. 2.3.2 мы ввели определение отображения Пуанкаре, создаваемого потоком в окрестности замкнутой траектории у системы (5.9.1). Отображение Пуанкаре можно рассматривать как дискретную динамическую систему, определенную на сечении S. По характеру поведения орбит этой динамической системы можно судить о поведении траекторий системы (5.9.1). Аналогичный подход мы будем использовать для исследований траекторий на хаотическом аттракторе М. Выберем подходящее сечение S - участок гиперповерхности 5:

S(xu ...,х,) = 0. (5.9.8)

dx. f. (x, a) >

dt 1

(5.9.9)

dx. f. (x, a)

Теперь будем интегрировать систему (5.9.1) до момента изменения знака Xi - а. Далее, перейдем к интегрированию системы (5.9.9) с шагом Ах, = а-х,-, причем начальные условия мы

Лежащая в аттракторе траектория Г, которая проходит через точку XoS, через определенное время пересекает сечение 2 в точке Xi = P(xo), затем в точке Ха = P(xi)= р2(хо) и т. д. Таким образом, мы получаем орбиту 0(хо) = {хо,Xi,Ха, ...} динамической системы, которая порождается отображением Р. По характеру орбиты 0(хо) мы можем до некоторой степени судить о геометрической структуре аттрактора s. Так, например, если орбита 0(хо) плотно заполняет некоторую дугу С, то дуга С является пересечением аттрактора с поверхностью S, и можно думать, что аттрактор si является двумерным. В частности, если точки орбиты О плотно заполняют замкнутую кривую (типа окружности), то можно считать, что аттрактор имеет вид двумерного тора, который плотно заполняется одной траекторией системы (5.9.1).

Обычный численный подход к нахождению орбиты отображения Пуанкаре заключается в том, что мы интегрируем систему (5.9.1) и на каждом шаге интегрирования оцениваем знак функции S в формуле (5.9.9). При изменении знака S мы находим точку пересечения Г с поверхностью 2 на основе интерполяции между двумя последними точками, найденными в процессе интегрирования. Очевидно, что грубая интерполяция будет источником численных погрешностей; для интерполяции более высокого порядка нам потребуется сохранять в ходе интегрирования большее число точек.

Нетрудно преобразовать процесс вычислений так, чтобы одна из точек, найденных численным интегрированием, оказалась прямо на 2 (см. [5.21]).

Вместо общего соотношения (5.9.9) рассмотрим сначала случай, чаще всего используемый на практике, а именно xi - - а = 0, где а - некоторая постоянная, а / фиксировано (1 / п).

Преобразуем систему (5.9.1) в эквивалентную систему, в которой роль независимой переменной вместо t играет х,. Разделим каждое уравнение системы (5.9.1) на г-е уравнение, причем будем предполагать, что /,(х, а)=#=0 в окрестности сечения 2. Тогда наша система преобразуется к виду

fn+i = Zf,{x, аУ§. (5.9.12)

Тем самым мы получаем новую систему из и -f 1 дифференциальных уравнений, причем начальное условие для неизвестной Хп+1 задается в соответствии с формулой (5.9.10).

Соотношение (5.9.8), описывающее гиперповерхность, имеет теперь вид x +i = 0. Далее мы поступаем точно так же, как это делалось ранее для плоскости х/ - а = О, полагая j = и -j- 1.

На рис. 5.34а - f приведены несколько периодических и одна хаотическая орбита отображения Пуанкаре для задачи 10. Гиперплоскость 2 определялась при этом уравнением у = 0. На рис. 5.34а изображена двухточечная орбита. Эта орбита возникла после бифуркации удвоения периода от основной ветви устойчивых периодических решений (см. рис. 5.26 из § 5.8). На рисунках 5.34b, с, d, е приведены орбиты отображения Пуанкаре, отвечающие периодическим решениям задачи 10 с периодами 4Т (возникающим после двух бифуркаций удвоения периода.- Ред.), 8Т, 16Г для разных значений параметрам На этих рисунках хорошо прослеживается эволюция, которую претерпевает орбита рис. 5.34а в ходе последовательных бифур-

Тем самым рекомендуется использовать запись (5.9.9) ровно на одни шаг. - Прим. ред.

будем брать в последней или в предпоследней точке, найденной интегрированием уравнения (5.9.1) Найденная таким образом точка лежит прямо на 2 (с точностью до погрешностей аппроксимации метода интегрирования). Тем самым мы находим следующую точку орбиты отображения Пуанкаре и можем продолжить интегрирование системы (5.9.1). Удобно использовать при этом какой-нибудь одношаговый метод, например, метод Рунге-Кутты с автоматическим изменением длины шага. Отметим, что если нам не нужно знать моменты времени, когда траектория системы проходит через сечение S, то последнее уравнение в (5.9.9) можно опустить.

В общем случае гиперповерхности (5.9.8) мы вводим еще одну переменную

х„+, = 5(х„ ...,х„) (5.9.10)

и добавляем к системе (5.9.1) дифференциальное уравнение вида

-%=/ +,(х. а), (5.9.11)

где

п

Г/IX, а;

7 = 1

каций удвоения периода. В результате этой последовательности бифуркаций орбиты становятся хаотическими, как это видно из

-48 -47 -4G А-48 -47 -46 А -48 -47 -46 А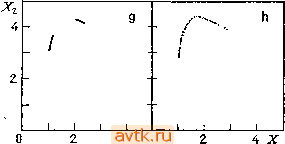

Рис. 5.34. Орбиты отображения Пуанкаре. Задача 10 (а - а= 16, 6 = 4, у = 0.а)г= 339,0, 6) г = 338,0, с) / = 334,5, d) г = 334,2, е) г = 333,25, f) г = 332,5. Задача 8, ,= 2 {g,h), Л = 2, В = 5,9, £>2 = 10Z>i; показана проекция орбиты с гиперплоскости - У1 + - Уг + 0,9 = О иа плоскость Xi - Xi. g) D, = 1,194, h) Z>, = 1,21.

рис. 5.34f, где изображена хаотическая орбита отображения Пуанкаре для значения параметра г = 332,5. Множество точек пересечения траектории системы (5.9.1) с гиперплоскостью S плотно заполняет дугу кривой, которая входит в пересечение

(общую часть) хаотического аттрактора с гиперплоскостью J.

Значения параметра г в бифуркационных точках удвоения периода образуют так называемую последовательность Фейгеибаума, стремящуюся к некоторому пределу (см. п. 2.5.3). Эти значеиия параметра г можно подсчитать с помощью алгоритмов, описанных в п. 5.8.5, и на их основе вычислить величины

(5.9.13)

Координаты точек бифуркации и значения б/ приведены в табл. 5.31 [5.26]. Из таблицы видно, что найденные значения 8j стремятся к пределу б* 4,6692 [5.27].

Таблица 5.31. Каскад бифуркационных точек с удвоением периода для модели Лореица, задача 10 (о = 16, 6 = 4, й = 1, лг = 3,82038).

На рис. 5.34g, h представлены две хаотические орбиты отображения Пуанкаре для задачи о двух связанных между собой реакторах (задача 8). Трехмерная гиперплоскость 2 задается при этом соотнощением - 71-1-2-У2 +0,9 = 0. Для более наглядного геометрического представления орбита О отображения Пуанкаре, лежащая в плоскости 2, обычно проектируется на какую-либо из координатных плоскостей. В данном случае орбита О спроектирована на плоскость -Хг (см. рис. 5.34g, h). Из рисунка ясно, что точки орбиты О располагаются на некоторой гладкой кривой (точнее, в ее очень малой плоскости). Показатели Ляпунова, которые подсчитывались с помощью подхода, описанного в п. 5.9.1, приведены в табл. 5.30 для значений параметров, указанных на рис. 5.34g, h. При этом положительное значение к\ указывает на наличие хаотического аттрактора.

Это название возникло в технической литературе при исследовании установившегося поведения модели (т. е. чаще всего устойчивого стационарного решения) в случае очень медленного изменения параметра.

2) Стационарное (в составе термина квазистационарное ) понимается как установившееся, не обязательно ие зависящее от времени. Квазистационарное поведение в некотором смысле близко к установившемуся. Авторы не пытаются дать здесь точное определение используемых понятий.- Прим. ред.

Точнее, мало отличается до тех пор, пока х(а)-асимптотически устойчиво. - Прим. ред.

5.10. КВАЗИСТАЦИОНАРНОЕ ПОВЕДЕНИЕ ДИНАМИЧЕСКИХ МОДЕЛЕЙ

Рассмотрим динамическую модель, зависящую от параметра а,

- = iix,a), (5.10.1>

для простоты считая параметр а скалярной величиной. До сих пор мы считали значение а постоянным. Однако в реальных ситуациях параметры системы часто изменяются в зависимости от времени. Рассмотрим очень медленное изменение параметра а со временем t, задаваемое либо соотношением

a=a{t), а'(01<1. (5.10.2)

либо как решение дифференциального уравнения

= {t,a). (5.10.3)

В обоих случаях мы предполагаем, что параметр а меняется со временем гораздо медленнее переменных состояния х. Возникающее в результате поведение системы мы называем квазистационарнымОбычно мы считаем, что правые части уравнения (5.10.3) не зависят от х, хотя включение х в описание изменений а не вызвало бы никаких затруднений.

Поясним это понятие для случая, когда в момент времени / = 0 мы находимся очень близко к устойчивому стационарному

решению х(а(0))системы x = f (х, а(0)) (х (0) х (а(0))). Тогда решение х(/) системы

- = f(x, ait)), х(0) = х(а(0)) (5.10.4)

мало отличается от функции х (а (0), где х (а) - устойчивое стационарное решение уравнения (5.10.1) при фиксированном а

Рассмотрим теперь частный случай общей эволюционной задачи, часто встречающейся в физических и биологических

приложениях. Решение в данном случае изменяется со временем в малой окрестности устойчивых ветвей на диаграмме решений, в малой окрестности аттракторов. Процесс эволюции системы можно представить в форме так называемой эволюционной диаграммы, на которой из диаграммы решений выделяются устойчивые части и на которой стрелками изображается эволюция установившегося решения во времени. Наряду с этими медленными изменениями отмечаются также быстрые переходы от решения, которое потеряло устойчивость, к следующему аттрактору. Для описания изменений параметра во времени чаще всего используются два вида зависимостей а(), а именно, линейный рост

a = ao-fai2 (S.IQ.S)

и экспоненциальный рост

a = aoe (5.10.6)

Расчет эволюционной диаграммы осуществляется сравнительно просто, однако требует довольно много времени. Для интегрирования уравнений (5.10.1) с параметром а, изменяющимся согласно формулам (5.10.5) или (5.10.6), можно использовать некоторые из методов, описанных в § 5.7. При этом необходимо применять методы с автоматическим изменением шага интегрирования, поскольку при динамическом моделировании ситуации, когда решение меняется весьма медленно, чередуются с ситуациями, когда имеют место быстрые переходы к другому режиму. Поскольку изменение параметра а происходит очень медленно, то приходится проводить интегрирование на большом временном промежутке, с тем чтобы значение параметра а изменилось достаточно заметным образом. Довольно часто приходится повторять процесс интегрирования с разными начальными условиями, особенно если характер квазистационарного поведения меняется в зависимости от выбора начального условия, что, как правило, имеет место для моделей с несколькими совместно существующими аттракторами.

Следующей проблемой является выбор скорости роста, т. е. фактически констант ai или с. Если выбрать их большими, то уже нельзя будет говорить о квазистационарном поведении системы, а изменение а будет происходить в тех же временных масштабах, что и изменение х. Если же выбрать ai и с слишком малыми, то непомерно возрастет время вычислений. Обыкновенно при выборе констант приходится останавливаться на некоторых компромиссных значениях, которые не оказывают влияния на поведение ветвей стационарных и периодиче-

Смысл этой фразы непонятен. Стационарными и периодическими решениями обладает система (5.10.1) при фиксированных а; от с и aj они-(эти решения) никак не зависят. - Прим. ред.

2> Здесь и ниже имеются в виду стационарные, периодические и т. д. решения (5.10.1) при постоянном а. - Прим. ред.

ских решений но которые могут влиять на скачки решений при переходе через точки бифуркации. При этом в зависимости от скорости изменения а мы можем получать различные продолжения решений на эволюционной диаграмме.

5.10.1. Типичные эволюционные диаграммы

Наиболее часто встречающимся типом квазистационарного поведения является перемещение решения вдоль выбранной устойчивой ветви решений (стационарных, периодических, ква-зипериоднческих, хаотических) 2) на диаграмме решений. В указанных случаях поведение системы предсказуемо - в нем не наблюдаются качественные изменения, скачки, быстрые переходы и т. п. Такого рода переходы (скачки) могут появляться только в точках бифуркации. Возможные способы перехода через эти точки изображены на рис. 5.35. Более сложные бифуркации периодических решений (например, удвоение периода возникновение хаотических режимов) на рисунке не показаны. Обсудим теперь отдельные типичные случаи, изображенные на рис. 5.35.

Случай а) соответствует точке ветвления на диаграмме стационарных решений. Решение x{t) системы x = f(x, а(/)) мало отличается от функции х(а(/)), где х(а) - стационарное решение системы x = f(x, а) (при постоянном а). После критического значения параметра а** решение пр одолжается вдоль устойчивой ветви стационарных решений х(а). Зависимость

х(а) в точке а** претерпевает излом. Однако прн построении эволюционной диаграммы с помощью динамического моделирования (численного решения системы x = f(x, а(/))) можно не-заметить, что произошел переход (перескок) на другую ветвь стационарных решений. В случае Ь) (бифуркация типа вилки) решение продолжается по одной из последующих устойчивых ветвей, выбранных случайным образом в зависимости от погрешностей аппроксимации и округления. В реальных физических или биологических проблемах удобно рассматривать соответствующую задачу как стохастическую; характер распределения флуктуации переменных состояния определяет тогд,а вероятности выбора отдельных ветвей решения.

ooo-ooooJ

.....

оси

Рис. 5.35. Схематическое изображение перехода через критические точки при квазистационарном поведении.

Иначе говоря, по окончании переходного периода решение х(/) может быть близко к некой ветви стационарных решений системы x = f(x, а), но может также совершать колебания, близкие к периодическим (или имеющие стохастический характер).

Случай d) соответствует бифуркации Андронова-Хопфа на устойчивой ветви стационарных решений. Случай е) аналогичен случаю с). При переходе а через критическое значение а* для ветви периодических решений (случай f)) поведение системы также аналогично случаю с): она эволюционирует по направлению к ближайшему аттрактору системы x = f(x, а).

Рассмотренные случаи представляют собой наиболее типичные участки эволюционной диаграммы. Ситуация может оказаться более сложной при появлении квазипериодических и хаотических решений.

При переходе с одной ветви решения на другую мы можем спрогнозировать следующую ветвь в представленных на рис. 5.35 случаях а) и d). Такие случаи мы будем называть детерминист-

Случай с) представляет особый интерес, поскольку мы не можем предсказать поведение системы без дополнительных сведений. После перехода а через критическое значение а* состояние системы сравнительно быстро изменяется, притягиваясь к наиболее близкому устойчивому состоянию. Этот притягивающий режим может описываться устойчивым стационарным, периодическим или хаотическим решением системы x = f(x, а).