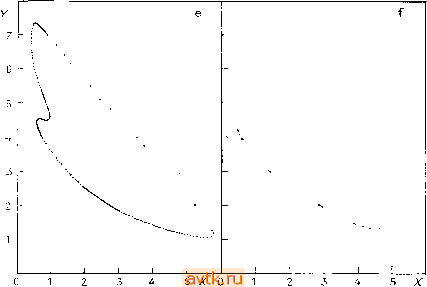Рис. 5.41. Орбиты отображения Пуанкаре системы (5.11.12); А - 2, 5 = 6. л) о = 0,7, m = 3: 7- периодическое решение, 6) о = 0,8, m = 3: 8-периоди-ческое решение, с) а = 0,9, со = 3: 9-периодическое решение, rf) а = 0,5, <й = 6: квазипериодическое решение, е) а = 0,6, m = 3: хаотический аттрактор, f) а= 1, (0 = 3: хаотический аттрактор.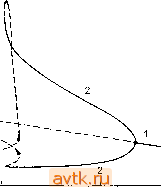

о

Рис. 5.42. Диаграмма 1- и 2-периодических решений системы (5.11.12); Л = 2, 5=6, (0 = 3; сплошные линии - устойчивые решения, штриховые - неустойчивые решения, - точка бифуркации удвоеиня периода.

бифуркации -Ь от 2-периодического решения ответвляется 4-периодическое (на рисунке оно не изображено). Отмеченный недостаток изображения на диаграмме решений проявляется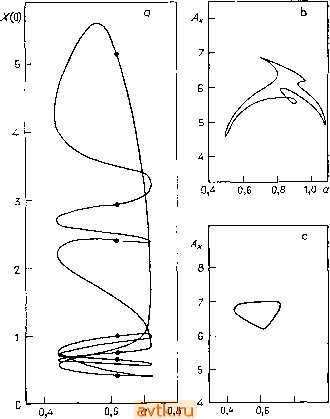

0,8 0-1,0

Рис. 5.43. Диаграммы -периодических решений для системы (5.11.12); Л = 2,. 5 = 6, со = 3, Ах - амплитуда переменной X. а) k = 7, точками обозначены решения, отличающиеся лишь сдвигом на 1/7 периода; Ь) = 6, с) k = 7,

ср. рис. а).

еще более заметно у А-периодических решений, где k достаточно велико. Примером служит диаграмма 7-периодического решения (рис. 5.43а), на которой каждое решение изображено семикратно (см., например, решение, обозначенное жирными точками). Если вместо Xifi) по оси ординат откладывать амплитуду периодического решения, то мы получим диаграмму

решений, представленную на рис. 5.43с. На рис. 5.43Ь приведена диаграмма 6-периодических решений.

При анализе периодических решений неавтономных систем мы сталкиваемся с проблемой, как найти какое-либо yfe-периоди-ческое решение, которое в дальнейшем могло бы служить для запуска алгоритма продолжения. При достаточно больших k вероятность наугад найти такое решение мала. Это утверждение иллюстрирует табл. 5.32, в которой приведены результаты применения метода Ньютона для системы уравнений (5.11.12) при случайном выборе начальных значений для переменных

Таблица 5.32. Применение метода Ньютона для нахождения й-периодического решения системы (5.11.12), Л = 2, В = 6, со = 3. Начальные значения выбирались случайным образом из указанных промежутков, для каждого k было выбрано 500 начальных точек

Область выбора Х(0); Уф); а

Число найденных fe-периодических решений

Найденные т-периодические решения, где k делится па тп

-10; 0-

1,5 1,5

Таблица 5.33. Некоторые Апериодические решения системы (5.11.12), А =2, В = 6, (о = 3

r\i=X{0), r\2==Y{0), а. В случае больших k ситуация осложняется тем, что мы можем, задав k, найти т-периодическое решение, где k делится на т (табл. 5.32 это подтверждает). В табл. 5.33 приведены найденные значения переменных для различных -периодических решений.

Нахождение точек бифуркации и -1 производится

совершенно аналогично тому, как это делалось в случае автономной системы. Ответвление 2-периодических решений в точке бифуркации -1 от семейства -периодических решений можно приближенно рассчитать с помощью метода, описанного в п. 5.4.2.

5.12. ЗАДАЧИ

Ниже приведено несколько задач для самостоятельного решения с помощью подходов, описанных в данной главе.

5.12.1. Постройте диаграмму стационарных решений для задачи 1, используя в качестве параметра переменную А. Используйте метод отображения параметра (см. § 5.2), выбирая последовательность значений в. Параметры задачи: 7 = 20, р = 0,. Da = 0,01, = 6; 7; 8; 10; 12. Покажите, что во всех указанных случаях существует интервал значений Л, при которых задача имеет три решения. На найденной зависимости решения от параметра укажите также характер устойчивости этого решения. Далее постройте эволюционные диаграммы для Л, возрастающих и убывающих со временем.

5.12.2. Рассчитайте диаграмму решений задачи 5 в зависимости от параметра Ki с помощью метода отображения параметра, описанного в § 5.2. Покажите, что при /(i = 10- существует три стационарных решения, два из которых являются устойчивыми. Укажите на каждой ветви решений характер их устойчивости. Затем постройте диаграмму решений в зависимости От параметра Cso при Ki = 10-.

5.12.3. Рассмотрим энзиматическую реакцию с конкурентным иигибированием субстратом

E-bS=!=ES-iE + P.

При этом для скорости реакции можно получить соотношение

s + Cs + cJi

Здесь V означает скорость реакции (в энзиматической кинетике обычно используется обозначение v (velocity) вместо г (rate)), Cs - концентрацию субстрата, а Umax, Ks, К\ - положительные параметры. Аналогичная формула может быть использована и для описания кинетики роста микроорганизмов, ингибирован-ных субстратом; при этом параметр Umax обозначается как ji (ср. задачу 6).

Уравнение баланса массы для реактора проточного типа с полным перемешиванием при постоянной температуре, объеме V, расходе F и концентрации на входе Cso может быть записано в виде

dc ~dt

maxsl

(5.12.2)

Вводя время задержки x=V/F и безразмерную концентрацию на выходе х= Csi/Cso, можно переписать это уравнение баланса в безразмерной форме

dx dt

= 1 -X-

аа + а^х+х'

(5.12.3)

Здесь мы использовали обозначения Оа=тиз^АГ Qosiso и ai = CsdKi-

Постройте диаграмму стационарных решений как функцию параметра Da при следующих значениях параметров: Cso = 5 и

5.12.4. Модель реактора проточного типа с перемешиванием, в котором происходят две последовательные ферментативные реакции

со скоростями, учитывающими ингибирование субстратом, можно представить в виде (системы) трех дифференциальных

уравнений

dt ~ V (Ао а) + -а'

в

dcz dt

- V (во в) ~Ь F

~ IF ipzG z) z

где

=-kx

si + A + dMii

Вводя переменные

A>

2 = -

tk,c

I-El

ao AO

перепишем исходную систему в безразмерной форме

da I /, ч 1 = -(1 -а) + г„,

dz \ , . ,

где

(5.12.4a)

(5.12.4b)

(5.12.4c)

(5.12.4d)

Ksi+a + aKa 1 b

n=--r

К /Cs2 + * + *V-i2 z~ a~b 0~Bo/AO 0~Zo/AO

(5.12.4e)

Рассчитайте диаграмму стационарных решений в зависимости от параметра т для следующих значений остальных параметров: Ksi = Ks2 = 0,l; &о==2:о = 0 и

a) Яп = 0,1,/С = 3, Ki2 = 0,01; 0,1; с ;

b) ii=i2 = 0,l,/С = 0,366; 1; 3;

c) Я.1 = 0,1, Я12 = 0,01, К = 0,3.

Используйте алгоритм продолжения, описанный в п. 5.2.3, либо метод отображения параметра (п. 5.2.1) по следующей схеме: выберите а, из первого уравнения (5.12.4d) подсчитайте т (положив d = 0), затем из второго уравнения (при & = 0) найдите значение параметра Ъ, последовательно подставляя ряд значений Ъ и используя метод Ньютона. Покажите, что существует несколько решений для некоторых интервалов значений параметра т (например, для т = 3 в случае с)). Определите характер устойчивости отдельных ветвей решения. Продумайте способ, как находить точки поворота. Попытайтесь построить соответствующую бифуркационную диаграмму в плоскости параметров {К - т).

5.12.5. Модель проточного реактора с перемешиванием, в котором происходят последовательные экзотермические реакции типа А->В->С, можно описать с помощью системы трех дифференциальных уравнений (см. п. 4.2.1):

=1 у 0аУехр-р:, (5.12.5а)

= -ir + Dayexp-p-Da5irexp, (5.12.5b)

= e p(e-0,) + DaBrexpy +

+ Da BaSW ехр , . (5.12.5c)

Здесь в - безразмерная температура, Y и W -безразмерные концентрации компонентов А и В. При этом предполагается, что рассматриваемые реакции имеют первый порядок.

Для построения диаграммы стационарных решений по параметру Da (остальные параметры фиксированы) можно воспользоваться следующим методом отображения параметра (при этом мы рассматриваем уравнения, у которых вместо левых частей стоят нули):

1. Из уравнения (5.12.5а) представим У как функцию от в.

2. Умножим уравнение (5.12.5Ь) на Ва и сложим с уравнением (5.12.5с). Из полученного соотношения определим W как функцию от в, используя при этом уже найденную зависимость У(0).

3. Обе эти зависимости подставим в уравнение (5.12.5с) и получим уравнение следующего типа:

a(e)Da2 + &(e)Da + c(e) = 0. (5.12.6)

4. Для каждого заданного значения в из квадратного уравнения (5.12.6) найдем Da.

Постройте указанным способом соответствующую диаграмму решений при у-оо, В = 10, a = b=:k= I, вс = О, 5 = 0,013. Покажите, что при Da = 0,06 существует пять стационарных решений задачи (5.12.5). Укажите на диаграмме характер устойчивости стационарных решений. Используйте также для построения диаграммы метод продолжения типа предиктор-корректор и сравните полученные результаты. Найдите пять стационарных состояний исходной задачи при у^оо; а = р = = k=l, 5 = 0,01; вс = 0; В =10,05; Da = 0,0705 и выясните характер их устойчивости (значения 0 для отдельных решений должны выбираться следующим образом: 0,55; 3,05; 5,15; 6,55; 9,6). Покажите, что три из этих решений являются устойчивыми, и с помощью динамического моделирования (численного интегрирования) уравнений (5.12.5) проверьте, что решение на них стабилизируется.

Далее, путем динамического моделирования уравнений (5.12.5) покажите, что для значений параметров у^оо] В = 14; Р = 3; вс = 0; =1; а = 5 = 0,03 и значений Da, выбираемых из интервала (0,165; 0,33), в данной задаче существует некоторый предельный цикл. Более подробные результаты, которые можно использовать для сравнения, приведены в работе: Н1а-vacek V., Kubicek М., Visnak К.: Chem. Engng. Sci. 27(1972), 719-742.

5.12.6. Постройте бифуркационную диаграмму в плоскости параметров р и Da для задачи 1. Выберите следующие значения остальных параметров: у = 20, Л = 1, вс = О, В = 6; 8; 10; 12. Для построения бифуркационной диаграммы воспользуйтесь методом отображения параметра; после преобразования уравнений выберите последовательность значений в, для каждого из них найдите значения Da и р из условий для точки поворота (бифуркации слияния) или условий для бифуркации Хопфа.

5.12.7. Постройте бифуркационную диаграмму в плоскости параметров p = Pi = P2 и Da = Dai=Da2 для задачи 2. Значения остальных параметров выберите следующими:

a) V = 1000, вс1 =вс2 = О, В = 22, Л = 1,

b) 7 = 20, вс1 = вс2 = -5, В = 8 (В =10), Л=1. Далее, для нескольких значений параметра р постройте диаграмму решний как функцию параметра Da.

5.12.8. Модифицированная модель Лотки может быть описана системой трех дифференциальных уравнений вида

x=\-bx - xy - gxy+ Z,

y = a{xy + d-y), (5.12.7)

z = f{gxy-z).

Одна из многочисленных модификаций уравнений Лотки - Вольтерры.

Выберите значения параметров равными а = 4, 6 = 0,35, d=0,l, f = 0,2. У данной модели существуют периодические решения, для некоторых значений параметра g они представлены в следующей таблице (для каждого решения указана одна точка на траектории. - Ред.):

Найдите периодические решения для этой модели как функции параметра g и постройте диаграмму периодических решений:

(Литература: Schulmeister Th. Chaos in a Lotka-Scheme with Depot. Stud. Biophys., 72(1978), 205-206; Хибник A. И. Периодические решения системы n дифференциальных уравнений.-НЦБИ АН СССР, Пущино, 1979.)

5.12.9. Одна из моделей хищник-жертва , используемых в математической экологии, может быть описана системой трех дифференциальных уравнений вида

Хх = дг, (дг, - Р) (1 - Хх) - Xiy - a (д:, - х^),

Х2 = Х2 {Х2 - Р) (1 - ДГа) - Х2У~а {Х2 - Xl),

y = y{xi + X2 - p - М).

(5.12.8)

Параметры задачи выбираются следующими: р = 0,25; а = = -0,02; ц = 0; р. У такой модели существуют периодические решения (Т - период), например,

Продолжите эти периодические решения по параметру р.

(Литература: Хибник А. И. Периодические решения системы п дифференциальных уравнений. - НЦБИ АН СССР, Пущино, 1979.)

5.12.10. Исследуйте уравнение Дюффинга специального вида:

118 2

x+gg-x-д-д: + -1д-> = -5-005(0/, (5.12.6)

где точка означает дифференцирование по t. Перепишите это уравнение второго порядка в виде системы двух уравнений первого порядка. Покажите, что для некоторых со из интервала (0,1; 2) существует несколько устойчивых периодических решений данной задачи (их можно найти с помощью динамического моделирования). Постройте диаграмму периодических решений в зависимости от параметра со.

(Литература: Rudiger Seydel. From Equilibrium to Chaos. Practical Bifurcation and Stability Analysis. Elsevier, New York - Amsterdam - London, 1988.)

5.12.11. Проанализируйте математическое описание задачи 6 с запаздыванием во времени в функции роста, задаваемой формулой (Р6-4). Выберите следующие значения параметров: р = 0,5; V/F = 3; Схо = 0,005, Cso = 5, = 0,03, Ki = 5, 5xs = = 0,5. В случае /l = 0 задача имеет два устойчивых стационарных решения, одно с низкой конверсией субстрата (Cs 5), другое - с высокой конверсией субстрата (cs 0). При возрастании величины запаздывания устойчивость первого решения не меняется, в то время как второе решение при t>t*0,19 становится неустойчивым и возникает установившееся периодическое решение. Используя стандартное программное обеспечение для интегрирования уравнений с запаздыванием, исследуйте указанную выше потерю устойчивости. Если в вашем распоряжении нет соответствующей стандартной программы, то воспользуйтесь методом Эйлера с интерполяцией по таблице значений (см. п. 5.7.4.4).

ЛИТЕРАТУРА

[5.1] Ortega J. М., Rheinboldt W. С: Iterative Solution of Non-linear Equations in Several Variables. Academic Press, New York, 1970. [Имеется перевод: Ортега Дж., Рейнболдт В. Итерационные методы решения нелинейных систем уравнений со многими неизвестными. - М.: Мир, 1975. - 558 с]

5.2 Schreiber I.: MS Thesis (на чешском), КРА VSCHT, Praha, 1979.

5.3 Wacker Н. (ed.): Continuation Methods. Academic Press, New York, 1970.

[5,4] Kubicek M., Holodniok M Marek I.: Numer. Funct. Anal, and Optimiz. 3 (1981), 223.

:5.5] Kubicek M.: ACM Trans. Math. Software 2 (1976), 98. ,5.6] Фаддеев Д. К., Фаддеева В. Н. Вычислительные методы линейной

алгебры. - М.-Л.: Фнзматгиз, 1963.- 734 с. [5.7] Демидович Б. П., Марой И. А. Основы вычислительной математики.- М.: Наука, 1966.