*> Имеются в виду точки на такой диаграмме периодических решений, которая различает два взаимно симметричных решения.-Прим. ред.

рое решение уравнений (5.5.1) с траекторией у, то P{t) = = {-x{t),-y{t),z{t)) - также решение (с траекторией g{y)). В частности, если P{t)-периодическое решение, то Р (/), очевидно, тоже. При этом могут иметь место два случая:

1- ff(V) = Y. т. е. решения Р и Р имеют одну и ту же траекторию, которая симметрична относительно оси г; при этом Р (t) = Р ( + Т/2). Такие решения мы будем обозначать символом S; примером служит решение, представленное на рис. 5.26Ь.

2. g{y)¥=y и, следовательно, функции Р и Р задают два существенно различных периодических решения, траектории которых у и g{y) взаимно симметричны относительно оси z (такие решения мы будем обозначать символом А). Примером может служить решение на рис. 5.26с.

Другие модели также обладают симметрией, в соответствии с которой с данным решением сосуществуют несколько других симметричных решений.

Опишем теперь зависимость периодических решений от параметра г для задачи 10, показанную на рис. 5.26а.

Из точки бифуркации Андронова-Хопфа субкрнтически отделяется ветвь неустойчивых периодических решений. С учетом упомянутой симметрии таких точек бифуркации оказывается две'> (на рис. 5.26а им отвечает одна точка), и из них ответвляются две ветви периодических решений, траектории которых взаимно симметричны по отношению к оси z. При уменьшении значения параметра г уменьшается расстояние периодических траекторий до состояния равновесия х = у - z = 0. Эти периодические траектории сходятся к двум гомоклиническим траекториям, которые входят и выходят из состояния равновесия X = у = z = 0 (мы обозначим их как yi и уг). Некоторые ветви периодических решений сходятся при изменении г к множеству, представляющему собой объединение этих гомоклиннческих траекторий, т. е. к множеству yiUy2- Амплитуда изменения переменной у на этом множестве вдвое больше, чем на одной гомоклинической траектории. На рис. 5.26а это отображено в виде скачка кривой.

На этом же рисунке в диапазоне параметра re(50,250) показано несколько точек поворота (где встречаются две ветви периодических решений). Вблизи каждой точки поворота существует узкий интервал изменения параметра г, в котором периодическое решение оказывается устойчивым. Отметим, что рис. 5.26 не показывает все существующие ветви периодических

решений [4.40]. Описание того, как периодическое решение теряет устойчивость, мы дадим в следующем пункте.

300 F Ау -

200 -

100 -

НВВ* i i 1 i i

-1 L

SO 1DD 150 200 250 300 350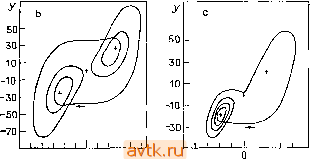

-БО -40 -20 о 20 40 а-

-40 -20

20 40 X

Рис. 5.26. Периодические решения задачи 10, а = 16, 6 = 4. а) Диаграмма периодических решений. Ау - амплитуда 2-й составляющей вектора решения, НВВ - точка бифуркации Хопфа, НО - гомоклиническая орбита, сплошная линия - устойчивое решение, штриховые линии - неустойчивые решения, - точка бифуркации с потерей симметрии. Ь) Симметричное устойчивое решение для значения г = 137; Т = 1,48629, Ау = 154. Показана проекция иа плоскость х - у, т) = (-0,02624, -36,5315, 135,279), стационарное решение, с) Несимметричное устойчивое решение для значения г = 87,487; Т= 1,54563; Ау = 101. Показана проекция иа плоскость х - у, г\- = (7,7979, -26,7059, 99,7729); + стационарное решение.

Верхние ветви решений, идущие из точек поворота, оканчиваются на разных гомоклинических траекториях, нижние же ветви на концах стремятся к паре гомоклинических траекторий ( восьмерка ). При г > 500 существует только одна ветвь пе-

риодических решений, которые являются устойчивыми и симметричными, при г ~ 470 эта ветвь теряет устойчивость в точке бифуркации с потерей симметрии. В табл. 5.24 приведены устойчивые периодические решения из всех устойчивых участков ветвей, показанных на рис. 5.26а, а также два неустойчивых периодических решения. Напомним, что устойчивые периодические решения можно искать также, имитируя (численно) динамику уравнений (5.8.1) (процесс установления периодического режима).

Таблица 5.24. Некоторые периодические решения для задачи 10)

>) (ж, у, г)-точка на траектории периодического решения.

) Устойчивое несимметричное решение после бифуркации с потерей симметрии.

Скажем теперь несколько слов о графическом представлении периодических решений и зависимости периодических решений от параметра. Периодические решения (некоторые их составляющие) мы либо представляем графически в зависимости от времени (см. рис. 5.27d), либо изображаем проекцию траектории на фазовую плоскость Xi - x,-, 1ф} (см. рис. 5.26Ь, с, а также рис. 5.27с). В последнем случае мы получаем представление о траектории, но теряем информацию о зависимости решения от времени. Для заданного периодического решения часто используется также проекция траектории отображения Пуанкаре на некоторую плоскость (см. § 5.9). При изображении диаграммы периодических решений (см. рис. 5.26а, 5.27а, b и 5.28) на оси ординат мы откладываем какую-либо величину, которая характеризует периодические решения в зависимости от параметра. Это может быть, например, координата какой-либо из неподвижных точек отображения Пуанкаре. Более наглядно изображение значений амплитуды (какой-либо пере-

менной) или периода отдельных решений. При этом в случае изображения периода для ветвей, которые возникли в точке бифуркации удвоения периода, мы вводим некий модифицирован-

С, 1,28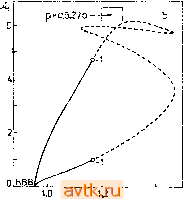

6 X,

1.А о,

Z 1

Рис. 5.27. Периодические решения задачи 8, N = % Л = 2, В - 5,9, р = = Di/D2 = 0,l. а) Диаграмма периодических решений. Л, -амплитуда переменной Хи сплошная линия - изолированное семейство периодических решений с периодом 7 ~ 11-13, штриховая линия -ветви периодических решений с удвоенным периодом Т ~ 22-26. О-1 точки бифуркации удвоения периода. Ь) Диаграмма периодических решений. Ai - амплитуда переменной Хи сплошная линия - устойчивое решение, штриховая линия - неустойчивые решения, НВВ - бифуркация Андронова - Хопфа, О-1 - точки бифуркации удвоения периода, с) Траектория периодического решения для значения параметра Di = 1,26. Т - 12,31918, Л, = 6,20, т) = (3,7335, 2,0840, 1,2159, 2,5000). Показана проекция иа плоскость Хх - Хг. d) Периодическое

решение с рис. с).

НЫЙ период (для ветви решения с периодом Tz 2Ti, которая отделилась от ветви решений с периодом Ти модифицированный период определяется как 2 = 2/2), в результате чего диаграмма остается в этих точках непрерывной.

Описанный выше алгоритм с успехом использовался также для изучения периодических решений в случае модели двух

связанных реакторов, в которых имеет место реакция типа брюсселятор (задача 8). На рис. 5.27а, b приведены две небольшие части диаграммы периодических решений для этой задачи. Изола, изображенная на рисунке 5.27а, содержит четыре точки поворота и очень близко к ним четыре точки бифуркации удвоения периода (последовательность дальнейших бифуркаций удвоения на рисунке не представлена). На части диаграммы.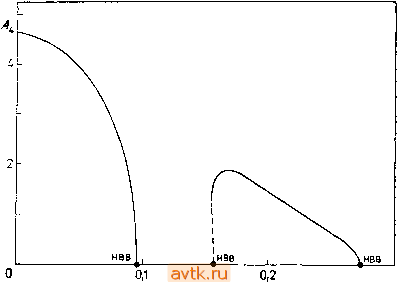

Da,. 0,3

Рис. 5.28. Диаграмма периодических решений задачи 2; у = 1000, В = 12, Pi = = 2, вс = О, Л = 0,8, Оэг = 0,2. Сплошные линии - устойчивые решения, штриховые линии - неустойчивые решения. А* - амплитуда переменной 02, НВВ - точка бифуркации Андронова - Хопфа.

представленной на рис. 5.27Ь, изображены две ветви, которые выходят из точки бифуркации Андронова-Хопфа, а затем вновь возникает последовательность бифуркаций удвоения периода (на рисунке показаны только точки первого удвоения). В целом диаграмма периодических решений оказывается гораздо более сложной, чем показано на рис. 5.27а,b (см. работу [5.29]). Точки бифуркации, изображенные на рис. 5.27а, мы рассмотрим в следующем пункте.

Диаграмма периодических решений для задачи 2 изображена на рис. 5.28а, Ь.

Для сильно неустойчивых периодических решений (мультипликаторы порядка 10 и больше) метод простой стрельбы не

работает. В таких случаях для процесса продолжения можно использовать разностные методы или метод многократной стрельбы. Метод многократной стрельбы можно применять также для продолжения периодических решений вблизи гомоклинических орбит. Таким способом можно находить периодические решения с ббльшими значениями периода Т, чем при использовании метода простой стрельбы.

При запуске процесса продолжения периодических решений нам необходимо определить начальную точку на ветви, т. е. лериодическое решение для одного значения параметра а. Относительно легко такое решение можно найти в окрестности точки бифуркации Андронова-Хопфа (х+, х+, х+, а+), методы определения которой изложены в § 5.5. Здесь используются, по существу, два подхода.

Первый из них основан на асимптотическом анализе характера ветвления в данной точке путем учета высших производных. Описание этого метода можно найти в работе [5.33], где приведен также собственно алгоритм вычислений, В результате мы получаем:

a) оценку периода Т;

b) возможность узнать, является ли ответвившееся решение устойчивым;

c) возможность определить направление ответвления, т. е. узнать, отходит ветвь периодических решений при а <. а+ или при а > а+.

Другой подход к данной задаче является эвристическим. Именно, делается попытка найти периодическое решение при <а, близком к а+ (см. п. 5.8.2). В качестве начального приближения для величины периода Т обычно годится величина f =

= 2я/д/ю , где Ai,2 = ±iV® - собственные числа матрицы Якоби правых частей в точке бифуркации Андронова-Хопфа. Начальное приближение ri можно выбрать, например, в виде

Т1, = Х+, . . ., Т1, , = Т1, = х+ + 6,

где 6=70 есть некоторое фиксированное малое число, а ri; в процессе ньютоновских итераций остается неизменным. В зависимости от того, будет ли этот выбор успешным для а = = a+-f б или для а = а+ -б, выясняется обычно, в какую сторону ответвляются периодические решения. Здесь 6=70 есть опять подходящим образом выбранное малое число. В целом указанный подход дает вполне удовлетворительные результаты.

5.8.5. Бифуркации периодических решений

При изменении параметра а устойчивость периодических решений на одной ветви решений может изменяться. Значения параметра, при которых меняется устойчивость и от исходной ветви решений отходит новая ветвь (т. е. бифуркационные значения параметра), характеризуются значениями собственных чисел матрицы монодромии В (5.8.17), лежащими на единичной окружности в комплексной плоскости. При изменении устойчивости одно или два собственных числа переходят через эту единичную окружность.

Если одно собственное число матрицы монодромии В проходит по вещественной оси через точку -1, то от ветви периодических решений отходит ветвь решений с двойным периодом (см. § 2.3). На рис. 5.29с схематически представлены некоторые возможные варианты такого ветвления, при этом если исходная ветвь была устойчивой, она эту устойчивость теряет, а устойчивость новой ветви определяется направлением ветвления. Бифуркация такого типа называется в литературе бифуркацией удвоения периода, или бифуркацией типа -1 . Указанная бифуркация обычно последовательно повторяется в достаточно узком интервале значений параметра а, образуя при этом так называемую последовательность Фейгенбаума (см. табл. 5.31). Описанная структура бифуркаций изображена на рис. 5.29d.

Другие явления возникают в случае, когда одно собственное число проходит по вещественной оси через точку -j-l; как правило, это соответствует точке поворота на диаграмме решений (рис. 5.29а). Если одна из ветвей отвечает устойчивым периодическим решениям, то другая отвечает неустойчивым. Более сложная картина наблюдается в системах, обладающих симметрией (см. задачу 10, которая рассматривается в п. 5.8.4). Схематически эта ситуация представлена на рис. 5.29Ь. От ветви устойчивых симметричных решений при бифуркации типа -f 1

Оба этих подхода оказываются слишком сложными в случае, когда разыскивается периодическое решение на устойчивой ветви. В этом случае достаточно просто интегрировать дифференциальные уравнения вплоть до установления колебаний. [)

Направления ветвлений в точках бифуркации удвоения периода или в точках бифуркации с потерей симметрии приближенно можно подсчитать с помощью методики, описанной в п. 5.4.2.

ОТХОДИТ ветвь устойчивых несимметричных решений. При этом исходная ветвь симметричных решений теряет устойчивость.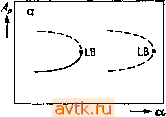

о.

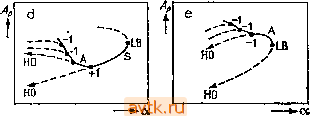Рис. 5.29. Схематическое изображение бифуркаций периодических решений; сплошные линии - устойчивые решения, штриховые линии - неустойчивые решения. Ар - амплитуда или какая-либо другая величина, характеризующая периодические решения, -fl-точка бифуркации с потерей симметрии, -1- точка бифуркации удвоения периода, LB - предельная точка (точка поворота), S - симметричное решение, А - асимметричное решение; а) точка поворота, Ь) точка бифуркации с потерей симметрии, с) точка бифуркации удвоения периода, d) последовательность бифуркаций, удваивающих период, которая следует за бифуркацией с потерей симметрии, е) последовательность бифуркаций, удваивающих период.

Следующий тип бифуркации возникает при переходе двух комплексно сопряженных собственных чисел через единичную окружность. Здесь от исходной ветви, которая утрачивает устойчивость, отходит ветвь двухчастотных колебаний. Более точно, рождается инвариантный двумерный тор, устойчивый или не-

устойчивый в зависимости от суперкритического или субкритического характера бифуркации (т. е. от того, что больше, а или а*; см. п. 2.3.1).

В качестве примера описанных бифуркаций обратимся вновь к рис. 5.26а для задачи 10, приведенному в п. 5.8.4. В окрестности каждой точки поворота на узком интервале изменения г существует устойчивое периодическое решение. Это решение теряет устойчивость либо через бифуркацию удвоения периода (в случае ветви несимметричных решений, см. рис. 5.29е), либо в точках бифуркации -4-1 с потерей симметрии (в случае ветви симметричных решений, см. выделенные точки на рис. 5.26а). За этой бифуркацией возникает последовательность бифуркаций типа -1 (см. рис. 5.29d). Кроме того, на основной ветви на рис. 5.26а при г 350 имеется последовательность бифуркаций удвоения периода. На рисунке для последней указаны только ветви решения с периодом 27 и ATt

В последнее время внимание исследователей уделялось, в основном, разработке новых методов нахождения точек бифуркации на ветвях диаграммы периодических решений. Опишем здесь два итерационных метода для нахождения точек бифуркации удвоения периода. Оба метода основаны на нахождении периодического решения, для которого один из мультипликаторов строго равен-1 [5.26].

Метод 1 (бифуркация -1 )

Пусть характеристический многочлен матрицы монодромии В есть P(A) = (-l) det(B -Я1).

Соответствующее характеристическое уравнение записывается в виде

Р (Я) = Г -f а,Я - -f ... -f а„ ,Я -f а„ = 0. (5.8.28)

Вычисление коэффициентов может производиться произвольным образом, например, с помощью методов, рассмотренных в § 5.3.

Для того чтобы матрица В соответствовала точке бифуркации типа -Ь, значение Я = -1 должно быть корнем уравнения (5.8.28), т. е. должно выполняться следующее соотношение:

Fn+iir\u ...,г\п,Т, a)=l-f Е(-1)а, = 0. (5.8.29)

Уравнения (5.8.19) и (5.8.29) представляют собой систему n-f-l нелинейных (алгебраических) уравнений относительно n-f-l неизвестных г\и щ-г, Цк+х, Цп, Т, а (неизвестную r\ii мы вновь считаем фиксированной и лежащей на искомом

Точнее, соответствующие значения TI2, Цз, щ, Т, a(i!]i -2). -Прим. ред.

Профиле). Для решения этой системы воспользуемся методом Ньютона. Первые п строк матрицы Якоби найдем с помощью соотношений (5.8.15), (5.8.16) и (5.8.22). Элементы последней строки dFn+\/dy\j, dFn+i/дТ, dFn+i/da можно вычислить, используя, например, соответствующие разностные формулы.

Метод 2 (бифуркация типа -1 )

Матрица монодромии В имеет в точке бифуркации удвоения периода собственное число, равное -1. Это означает, что существует не равный нулю вектор \ = {vu у„), для которого

(B + I)v = 0. (5.8.30)

Вектор V, задаваемый системой (5.8.30), определен с точностью до некоторого множителя. Поэтому одну составляющую вектора V мы можем считать фиксированной в ходе всего процесса вычислений, положив, например,

Vs=l, (5.8.31)

где 1 S /г. Тем самым мы получаем 2п уравнений (5.8.19), (5.8.30) относительно 2п неизвестных rii, ris-i, Цк+\, Цп, Т, а, Vu Vs-i, Vs+i, Vn. Для решения этой системы вновь, как и в методе 1, воспользуемся схемой Ньютона. При этом по аналогии с методом 1 часть матрицы Якоби вычислим с помощью соотношений (5.8.15), (5.8.16), (5.8.22), а оставшуюся часть с помощью соответствующих разностных формул (существует также возможность их аналитического вычисления).

Проиллюстрируем описанные методы на примере задачи 8, в которой рассматривалась модель двух связанных между собой реакторов. На рис. 5.27а была представлена диаграмма периодических решений для этой задачи, на которой появились четыре точки бифуркации типа -1 . Координаты этих точек') приведены в табл. 5.25. Для точного определения критического значения параметра a = Dai и соответствующего периодического решения в одной из бифуркационных точек были применены оба описанных выше метода. Результаты расчетов представлены в табл. 5.26 и на рис. 5.30. Четыре строчки таблицы отвечают одному и тому же периодическому решению, более точно - четырем периодическим решениям, отличающимся лишь сдвигом во времени. То, что таких решений при гц = 2 должно быть ровно 4, очевидно из рисунка.