скими. Остальные случаи, в которых последующая ветвь выбирается с локальной точки зрения случайно (случаи Ь), с), е), f) на рис. 5.35), мы будем называть стохастическими переходами. Отметим, что стохастический переход может давать в той или иной степени детерминированное продолжение. Это, например имеет место в случае с) на рис. 5.35, если при а > а* существует единственный аттрактор системы x = f(x, а).

Переходы в стохастическом случае могут быть очень быстрыми, однако могут происходить и в течение достаточно долгого времени. При этом переменные состояния не обязаны меняться монотонно.

Если одновременно существует несколько устойчивых реще-ний задачи, то в инженерной практике мы часто сталкиваемся с проблемой реализации выбранного стационарного рещения путем соответствующего медленного изменения параметра (для которого такое изменение удается осуществить). Принимая вО внимание то, что начальные условия для переменных состояния часто с трудом поддаются регулированию, этот вопрос оказывается чрезвычайно важным. Типичным примером здесь служит проблема перевода химического реактора в режим с высокой степенью конверсии с помощью изменения того или иного параметра, например, времени задержки.

5.10.2. Примеры эволюционных диаграмм

Рассмотрим теперь на примерах некоторые наиболее характерные типы эволюции системы при медленном изменении параметра, т. е. соответствующие эволюционные диаграммы. На рис. 5.36 представлены шесть случаев, когда при переходе через точку поворота или точку бифуркации Андронова-Хопфа происходит резкое изменение (скачок) решения. На рисунках изображены перескоки при увеличении или уменьшении значений параметра со временем. На рис. 5.36а и 5.36b приведены наиболее типичные случаи так называемого явления гистерезиса. Случай двух петель гистерезиса представлен на рис. 5.36с. Общим для всех трех случаев является то, что с помощью соответствующих изменений параметра здесь можно получить все устойчивые стационарные решения. Иначе обстоит дело в случае, изображенном на рис. 5.36d: здесь нельзя с помощью изменения параметра т во времени достигнуть верхнего устойчивого стационарного состояния, отправляясь от нижнего (при изме-нении т решение остается на нижней устойчивой ветви). Верхнего же состояния можно достигнуть путем изменения начальных условий или какого-либо другого параметра задачи. Аналогичная ситуация имеет место на рис. 5.36 е, f. Читатель может

0,01 0,1 1 Т 10 0,01 0,1 1 ТГ 10

0,01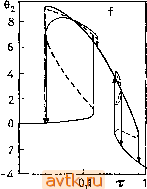

1 0,01

Рис. 5.36. Скачки в точках поворота и точках бифуркации Андронова - Хопфа на диаграммах решений при изменении параметра; сплошные линии - устойчивые стационарные решения, штриховые - неустойчивые стационарные решения, а) Задача &, V = 12, 60 = 0.005, с^о = 5, А = 0,5, = 0,03, /fj = 5, Sg = 0,5. b) Задача 5, см. параметры в табл. 4.1. с) Задача 1, у =

= 20,5=10, Л=1, Ос =-5, ko = l,a = l. d) Задача 1, у = 20, 5 = 10, Л = 1, вс = -5, feo = 1, а = 2,5. е) Задача 2, у = 20, 5 = 10, вех = &с2 = -5, а=1, ka = 0,5. f) Задача 2, у = 20, 5 = 10, вс1 = Осг = -5, а = 1, feo = 0,6.

легко установить, какие именно устойчивые состояния могут быть достигнуты путем медленного изменения параметра т

На рис. 5.37 изображена эволюционная диаграмма для задачи 2, где существуют устойчивые периодические решения. На нем видно влияние выбора величины 1 в формуле (5.10.4) (скорости изменения параметра а во времени) при о = = Daio = 0. В случае, представленном на рис. 5.37а, эта скорость была выбрана слишком большой, так что процесс не смог достаточно стабилизироваться.

Аи 41-

О 4 Аи

г

г^ = 500

г;=10ооо

0,3 .Dat)

Рис. 5.37. Эволюционная диаграмма задачи 2. у = 1000, В = 12, Pi = Pj = = 2, Qci = вс2 = О, Л = 1, Daj - 0,2, At = амплитуда переменной вг; а) Dai = 0,0007Л Dai = 0,000035/.

Поучительно сравнить эволюционную диаграмму рис. 5.37b с бифуркационной диаграммой по параметрам Daj и Оаг на рис. 5.20с, где видны точки бифуркации Андронова-Хопфа. На рис. 5.37b показано резкое нарастание амплитуды колебаний вблизи ВаГ 0,1574. Обращаясь к рис. 5.28, мы видим, что этому значению Dat отвечает бифуркация Андронова-Хопфа с жесткой потерей устойчивости стационарного режима (ветвь периодических решений отходит в сторону Da, < Dal* ).

Интересное поведение решения можно наблюдать в случае системы двух связанных между собой реакторов (задача 8). Выберем значения параметров из диаграммы стационарных решений на рис. 5.6, а именно, положим А =2, 6 = 6, D1/D2 = 0,1. Исследуем поведение системы при изменении параметра Di,

Сведений только о стационарных состояниях для этого, конечно, недостаточно.- Прим. ред.

А

2 О

ОСР

ТБХ

НСР

ОСР

0,001 ао1 0,1 1 z?i

Рис. 5.38. Эволюционная диаграмма задачи 8. N = 2, Л = 2, В = 6, р = = Z),/Z)2 = 0,1. а) Z), = 0,006-2/=°, 6) D, = 1,5-2-/°. ТБХ -точка бифуркации Андронова - Хопфа, НСР - неоднородное стационарное решение, ОСР - однородное стационарное решение, (g) - однородное периодическое решение, О - неоднородное периодическое решение, S - старт при / = 0.

шееся вследствие симметрии системы. При дальнейшем увеличении Dl происходит перескок на неоднородное стационарное решение, затем в точке комплексной бифуркации появляется неоднородное устойчивое периодическое решение. Это решение через каскад бифуркаций, удваивающих период, порождает хаотическое решение, которое в конце концов утрачивает устойчивость и мы вновь получаем однородное периодическое решение. При уменьшении Di (см. рис. 5.38b) однородное периодическое решение переходит прямо на неоднородное стационарное

Последние события иа рисунке ие отражены. - Прим. ред.

выбрав начальные условия в виде

= 0:Х, = 2,1, У, = 2,9, Х2=1,9, 2 = 3. (5.10.7)

При этом параметр D, будем изменять во времени по формуле

D, = D,o2-°. (5.10.8)

Эволюционные диаграммы приведены на рис. 5.38. В случае возрастающих Di (рис. 5.38а) при Di 0,01 мы имеем однородное периодическое решение (Z, = 2, Yi = Y2), получаю-

решение, затем в точке комплексной бифуркации на неоднородное периодическое решение и, наконец, вновь на однородное периодическое решение.

На рис. 5.39 изображена эволюционная диаграмма для задачи 10. В случае а) параметр г (число Рэлея) возрастает со временем в области, где стационарное решение в точке субкритической бифуркации Андронова-Хопфа (г - 33,45) теряет устойчивость, и система переходит в хаотический режим. Из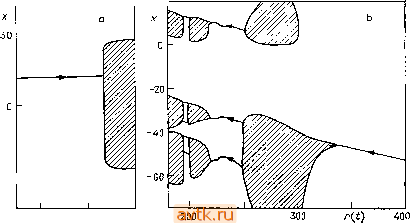

-30 -

35 r(t) 37

Рис. 5.39. Эволюционные диаграммы задачи 10, о = 16, 6 = 4. а) r(t) = = 32 -- 0,0005i. Приведены значения переменной х. В заштрихованной области траектория идет по хаотическому аттрактору, причем эта область представляет собой приближенную проекцию указанного аттрактора на ось х. Ь) /(;)= 400 - 0,1/. Показаны величины проекции орбит отображения Пуанкаре на ось X. Сечение 2 определяется уравнением I/ = 0. В заштрихованных областях траектория системы идет по хаотическому аттрактору.

рисунка видно, что система еще некоторое время, зависящее от скорости изменения г, следует ветвью неустойчивых (для г > > 33,45) стационарных решений, прежде чем ее поведение станет хаотическим.

На рис. 5.39b параметр со временем убывает. Сначала система устанавливается (приближенно) на периодическом решении, затем происходит удвоение периода, потом следующее удвоение и так далее - до тех пор, пока поведение системы не станет хаотическим. Хаотическое поведение наблюдается до значения г, приблизительно соответствующего точке поворота на ветвь устойчивых периодических движений (г 248) (ср. рис. 5.26а). После этого поведение системы становится (приближенно) периодическим и хаотический аттрактор перестает

В приложениях чаще всего встречается случай периодического (внешнего) воздействия иа динамическую систему, когда функция f представляет собой периодическую функцию переменной t с периодом Т, т. е. когда для любых , х и а имеет место соотношение

i(t + T, X, a) = f(, X, а). (5.11.2)

При этом периодическое решение системы (5.11.1) обычно удовлетворяет условию

x(t + kr) = x(t), (5.11.3)

где k - натуральное число. Такое решение мы будем называть -периодическим.

Отметим, что могут существовать системы типа (5.11.1), для которых условие (5.11.2) выполняется, имеющие решение периода (О ф kT.

Примером такого рода служит система

x = y + ix + y-l)sin2nt, У = ~х,

для которой Т=\, а ее периодическое решение х = -cos , у = sva.t имеет период, равный 2л;.

В данном случае в точках траектории указанного периодического решения (т. е. в точках окружности х^-\-у^=\) правые части системы не зависят явно от времени t. Оказывается, что подобная ситуация имеет место для любой периодической

быть аттрактором . При г ~ 230 возникает бифуркация с потерей симметрии (излом на соответствующей кривой), затем опять происходит каскад бифуркаций удвоения периода и, наконец, вновь наступает хаотический режим. Указанная ситуация, т. е. движение системы вдоль ветви устойчивых периодических решений, возникает еще раз при г 198. При дальнейшем уменьшении г система вновь ведет себя хаотически.

5.11. РАСЧЕТ И АНАЛИЗ ПЕРИОДИЧЕСКИХ РЕШЕНИИ В НЕАВТОНОМНЫХ СЛУЧАЯХ

В § 5.8 мы исследовали случай, когда правые части системы дифференциальных уравнений (5.8.1) ие зависели явно от t. Во многих задачах, однако, время t в правых частях появляется, и система оказывается неавтономной:

i(t, X, а); xeR (5.11.1)

системы, которая обладает решением с периодом, несоизмеримым с периодом правой части системы.

В п. 2.3.2 было введено определение отображения Пуанкаре для случая автономной системы. В случае периодической неавтономной системы ее решения определяют некоторое отображение Р, которое называется отображением за период; мы будем его иногда также называть отображением Пуанкаре.

Опишем, как возникает такое отображение Р. Зафиксируем в системе (5.П.1), (5.11.2) некоторое конкретное значение параметра а. Возьмем произвольную точку R ; пусть x(/; Хо есть решение системы (5.11.1). Положим

Р(хо) = х(Г; Хо). (5.11.4)

Определенное таким образом отображение Р обладает теми же свойствами, что и отображение Пуанкаре из п. 2.3.2. В частности:

1. Неподвижной точке хо отображения Р соответствует 1-периодическое решение системы (5.11.1), так как Р (хо) = Хо- - -- ->х(Г;хо) = Хо.

2. Если система (5.11.1), (5.11.2) (при фиксированном а) имеет А-периодическое решение, то k-я итерация, отображения Р имеет неподвижную точку, поскольку если х(АГ;хо) = Хо, то

РМХо)=Хо.

3. Устойчивость периодического решения определяется устойчивостью соответствующей неподвижной точки отображения Р или Р*.

Так же, как в автономном случае, мы в принципе имеем две возможности для нахождения периодического решения при фиксированном а, т. е. решения нелинейной краевой задачи (5.11.1), (5.11.3), где k заранее фиксировано. Первая из этих возможностей связана с применением разностных методов (ср. с соотношением (5.8.6)). Другая возможность заключается в использовании метода стрельбы и связана с выбором начальных условий

xi{0) = ni, /=1, 2, п. (5.11.5)

Решая уравнение (5.11.1) при условиях (5.11.5), находим при t = kT (ищем -периодическое решение):

XilkT) = (Ль . . ., Лп, а), /=1,2.....п. (5.11.6)

Для выполнения граничных условий (5.11.3) потребуем, чтобы

Pi (Ль , Лп, а) = ф| (л,-, ..., Лп, а) - Лг = 0. i = 1, 2, ...,п.

(5.11.7)

irZTP Р./(0) = 6./, (5.11.8)

4r = ts + % ЯЛ0) = 0. (5.11.9)

s = l

Устойчивость найденного периодического решения определяется его мультипликаторами - собственными числами матрицы монодромии

B = [d<pt/dn,] = [paikT)]. (5.11.10)

Таким образом, изменение характера устойчивости периодического решения вновь оказывается возможным лишь при переходе мультипликатора через единичную окружность. Переход через --1, так же как и в автономном случае, указывает на наличие точки поворота или точки бифуркации на зависимости решения от параметра. Переход через - 1 дает нам ответвление ветви периодических решений с двукратным периодом, т. е. периодом 2кТ.

Отображение Пуанкаре Р, определенное соотношением (5.11.4), при численном интегрировании системы (5.11.1) реализуется с помощью отображения <р, задаваемого формулой (5.11.6) при k=l. Выбрав точку i\ = rf, мы (приближенно) получим траекторию отображения Пуанкаре rf, т).....л'-

т,+1 =ф(л', а). (5.11.11)

Изобразив на плоскости две выбранные координаты точек т) (/ = 0, 1, 2, ...) траектории отображения Р, получим проекцию этой траектории на заданную плоскость. Так же, как в автономном случае, процесс может стабилизироваться, и мы будем последовательно (многократно) находить совокупность k точек; этой совокупностью будет характеризоваться А-периодическое решение системы (5.11.1). Если же эти точки образуют в пло-

Полученная система представляет собой систему п нелинейных уравнений с параметром а, и для ее решения мы можем использовать методику, описанную в § 5.1, а для продолжения решения по параметру-алгоритм DERPAR, описанный в § 5.2. В отличие от автономного случая, где период не был известен и поэтому одну составляющую щ мы считали фиксированной, здесь период кТ задается заранее, а все составляющие вектора ц неизвестны. Производные ,функций Ft мы опять находим с помощью проварьированных переменных pi,-dxi/dr\j, qi = = dxi/da и уравнений в вариациях

dpi, А df.

СКОСТИ замкнутую кривую, то скорее всего речь идет о квазипериодическом решении. Третья возможность состоит в том, что решение стабилизируется на хаотическом аттракторе; в этом случае траектория отображения Пуанкаре имеет более сложную структуру. Проиллюстрируем сказанное на примере задачи о реакторе с перемешиванием, в котором происходит реакция типа брюсселятор (ср. задачи 7, 9), находящаяся под влиянием некоторого внешнего воздействия. Предположим, что из-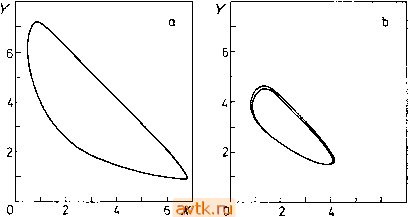

Рис. 5.40. Траектории периодических решений системы (5.11.12); Л = 2, S = 6, (О = 3, а) а = О, 6) а = 1,7084.

менение концентраций при этом описывается дифференциальными уравнениями вида

= A-{B+l)X + XY + a sin mt, = BX- J2y,

(5.11.12)

где a - амплитуда и <в - частота внешнего воздействия. Выберем значения параметров (концентраций подаваемых компонентов), полагая Л =2 и 6 = 6. Читатель может легко убедиться, что система (5.11.12) при а = 0 (при отсутствии внешнего возбуждения) имеет неустойчивое стационарное решение Х = А, У = В/А, около которого существует устойчивое периодическое решение с периодом Т = 5,0953 (собственная частота (Do = 2л;/7= 1,23313). Траектория этого решения изображена на рис. 5.40а. На рис. 5.40Ь представлено 1-периодическое решение для случая, когда имеет место синхронизация с внешним воздействием.

На рис. 5.41а - d приведены траектории отображений Пуанкаре установившихся периодических решений, а также квазипериодического решения. В случае -периодического решения здесь отмечено k точек траектории отображения Пуанкаре. На рис. 5.41е, f представлены примеры траекторий отображения Пуанкаре, которые определяют хаотический аттрактор. При сильном увеличении отдельного участка рис. 5.41е (или i) можно было бы увидеть сложную структуру хаотического аттрактора.

На рис. 5.42 изображены зависимости 1- и 2-периодических решений от параметра а (амплитуды внешнего возбуждения). При этом на графике зависимости Х(0) от параметра а каждое 2-периодическое решение изображено дважды. В точках

J L.

-J I I I L

У

-J-1 I I L