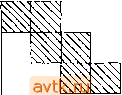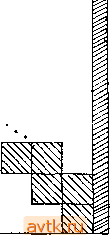Рис. 5.23. Схема размещения для системы (5.8.6), (5.8.7).

ЧТО выбор значения указанной переменной связан с известным риском: при неудаче мы не знаем, является ли она следствием расходимости выбранного итерационного метода или же результатом неудачного выбора этой переменной.

Для решения системы нелинейных уравнений (5.8.6) - (5.8.7) можно воспользоваться, например, итерационным методом Ньютона. Матрица размещения для этих уравнений является почти ленточной (ленточный характер нарушается лишь вхождением неизвестной Т и условиями (5.8.7), см. рис. 5.23). Для решения линейных систем в случае ленточной матрицы обычно используется одна из модификаций метода исключения Гаусса.

Предполагается, что система (5.8.1) имеет (при фиксированном а) лишь конечное число замкнутых траекторий. - Прим. ред.

Соотношения (5.8.6), (5.8,7) представляют собой систему л(Л'+1) нелинейных уравнений относительно п(Л'+1)+1 неизвестных х , х', ..., х', Т. Одну из неизвестных мы можем фиксировать заранее (это не может быть Г, поскольку периодическое решение существует только при дискретных, заранее неизвестных значениях Т Однако для того, чтобы такой подход был успешным, это фиксированное значение должно соответствовать существующему периодическому решению. Ясно,

х2 У^Г

Для уменьшения числа решаемых уравнений можно использовать неравномерную сетку узловых точек на интервале [О, !] Можно также вместо схемы 0{h) в формуле (5.8.6) использовать схемы высших порядков.

В табл. 5.22 приведены полученные в результате профили периодического решения (при различных значениях шага сетки h) для случая задачи 10 {х = хи у = Хг, г = хз). Сравнивая

Таблица 5.22. Профили периодического решения, найденные разностным методом (5.8.6), (5.8.7) (задача 10: а = 16, 6 = 4, г = 200,0). Значение x(t = 0) = О в ходе итераций фиксировано (т е [О, 1], < = Гт).

значения периода Т, полученные для различных величин шага Л, мы видим, что при уменьшении шага Л период Т стремится К некоторому предельному значению, приближенно равному Т'ке == 0,8226. Этот предел получается экстраполяцией по Ричардсону нз значений Т прн h = 0,005 и Л = 0,0025. Сравнивая теперь найденные значения периода Т с результатами, полученными с помощью метода стрельбы (см. табл. 5.24), мы видим, что точность, обеспечиваемая разностным методом, является не очень высокой.

5.8.2. Метод стрельбы

Другим подходом, используемым для вычисления периодических решений, является переход от краевой задачи к задаче Коши, или метод стрельбы. Выберем для нашей задачи некоторые начальные условия вида

. (0) = т)ь -=1,2.....п (5.8.8)

и определенное значение периода Т. Тогда систему дифференциальных уравнений (5.8.4) можно проинтегрировать от точки z = 0, где мы имеем полные начальные условия (5.8.8), до точки г=1, используя при этом методы, описанные в § 5.7. (В случаях, когда задача Коши более устойчива в отрицательном направлении, используется интегрирование от г == О до Z - -1. Читатель может легко внести в алгоритм соответствующие изменения.) В результате интегрирования мы получаем значения неизвестных х,- в точке 2=1:

xiil) = ((>i{m, ...,Цп, Т), /=1,2,..., п. (5.8.9)

Для выполнения условия (5.8.5) необходимо, чтобы удовлетворялась система п нелинейных уравнений

Р{{Ць Цп, 7) = Фг(Пь Цп, Т) - г]1 = 0, i=l, 2, п

(5.8.10)

относительно п+1 неизвестных гц, ..., ti , 7. Так же, как и в случае разностных методов, нужно задать произвольно значение одной из неизвестных. Выберем в качестве такой неизвестной переменную Цк и положим jn = Этот выбор будет успешным лишь в случае, когда fj лежит на искомой зависимости Xk.{z), т. е. когда при некотором ze[0, 1] выполнено соотношение fjft = Xft(z) (см. рис. 5.24). Для решения системы нелинейных уравнений (5.8.10) относительно неизвестных rii, ...

Пй-ь Лй+ь > Цп,Т воспользуемся методом Ньютона. При этом соответствующая матрица Якоби будет включать в себя

элементы dFi/dx\j {j ф k) и dFi/дТ. Эти элементы можно вычислить либо с помощью разностных формул, когда мы решаем задачу Коши (т. е. вычисляем Fi) для одной итерации в общей сложности п+ 1 раз (см. § 5.1), либо с помощью соответствующих вариационных переменных и системы дифференциальных уравнений в вариациях. Покажем, как это можно сделать в по-

v-min

Рис. 5.24. Схематическое изображение адаптивного выбора т).

следнем случае. Для этого, рассматривая х как функцию tj, введем обозначения

Pi = 2, (5.8.11)

Дифференцируя уравнение (5.8.4) по переменной г\ находим

(5.8.12)

Далее, дифференцируя (5.8.4) по Т, для производных qi - = dXi/дТ получаем

= + /=1, 2, (5.8.13)

Начальные условия для этих уравнений в вариациях имеют вид РцФ)-Ь,;, 9И0) = 0, (5.8.14)

где б,/ -символ Кронекера (равный О при ьф] ъ 1 при i = j).

= qdl) = fi{x(\), а), i=l,2,...,n. (5.8.16)

Из последней формулы следует, что уравнения (5.8.13) интегрировать не нужно, поскольку достаточно знать лишь концевое значение х(1).

Заметим, что столбец производных дР/дцц матрицы Якоби также оказывается ненужным, поскольку значение уже зафиксировано. Выбор этого значения r\k является довольно непростым делом, если только не использовать какую-либо априорную информацию об искомых периодических решениях (вытекающую, например, из неких физических соображений).

Если никакой предварительной информации у нас нет, то можно воспользоваться поисковым подходом, описанным в § 5.1, т. е. случайным выбором начальных приближений (всех Ль ..., Цп, Т) для метода Ньютона в сочетании со случайным выбором индекса k. В настоящее время, когда требуемый объем машинного времени перестает быть ограничивающим фактором, указанный подход становится, по-видимому, вполне реалистичным.

Пример сходимости метода Ньютона для задачи 10 показан в табл. 5.23. При этом, хотя начальное приближение выбиралось вблизи устойчивого периодического решения (ср. четвертое решение в табл. 5.24), метод привел к неустойчивому периодическому решению ( дважды повторенному - его минимальный период вдвое меньше найденного). Это обстоятельство, по-видимому, вызывается существованием в рассматриваемой области большого числа периодических решений (см. рис. 5.26). Оно подчеркивает преимущества продолжения периодических решений (см. п. 5.8.4) по сравнению с поиском решений для отдельных значений параметра.

Метод стрельбы является эффективным в тех случаях, когда соответствующие задачи Коши легко интегрируются. Если же функция x(z) сильно зависит от tj, то задача Коши становится плохой и сам метод уже не работает; в частности, так обстоит дело в случае сильно неустойчивых периодических решений. При этом в качестве альтернативного метода можно

Эти равенства сразу вытекают из исходной записи (5.8.4) (но могут быть, конечно, выведены и из (5.8.13)).-Прим. ред.

Для элементов матрицы Якоби системы (5.8.10) имеют место соотношения

= 1, j=l,2,...,n, (5.8.15)

Таблица 5.23. Метод стрельбы для нахождения периодического решения задачи 10: а = 16, 6 = 4, г = 197, т) = -5,5, k= I. Найденное неустойчивое решение составлено из двух идентичных периодических решений с периодом Г/2

использовать либо разностный метод, либо метод многократной стрельбы (см. п. 5.8.6).

5.8.3. Устойчивость периодических решений

Исследуем теперь устойчивость уже известного периодического решения, характеризующегося значениями iji, ..., fj , Т (см. п. 5.8.2).

Орбитальная устойчивость исследуемого периодического решения определяется собственными числами матрицы монодро-мии (см. (5.8.9) и § 2.3)

d<fi

= [р (1)].

(5.8.17)

При этом вариационные переменные pijiz) (5.8.11) находятся для значений т] и 7, отвечающих изучаемому периодическому решению. Напомним, что для нахождения собственных чисел матрицы В можно использовать методику, описанную в § 5.3. В случае автономной системы одно собственное число всегда равняется единице (Xi = l). Остальные п-1 собственных чисел Ki, Я„ (которые мы в гл. 2 называли мультипликаторами) соответствуют собственным числам линейной части отображения Пуанкаре и определяют устойчивость периодического решения. При этом периодическое решение является устойчивым (точнее, орбитально асимптотически устойчивым), если выполняются неравенства

\Xi\<l, 1 = 2, ...,п. (5.8.18)

Периодическое решение является неустойчивым, если хотя бы для одного мультипликатора имеет место условие Я(> 1. Если

с начальными условиями

/-г(0) = 0. (5.8.21)

К формулам (5.8.15) и (5.8.16) следует теперь добавить соотношения

= г,(1), /=1,2,..., п. (5.8.22)

Успешно продолжать решение системы (5.8.19) (т. е. двигаться вдоль (связной компоненты) кривой (5.8.19).- Ред.) можно до тех пор, пока щ будет лежать на профиле Хй(г) (см. рис. 5.24). Если же щ покинет профиль Xk{z), т. е. при данном выборе fife периодическое решение не будет существовать.

;>:, 10-*-10~, МОЖНО говорить о сильно неустойчивом перио-дическдм решении. В п. 5.8.5 мы рассмотрим различные случаи изменения устойчивости периодических решений при изменении параметров задачи.

5.8.4. Продолжение периодических решений по параметру

Займемся теперь исследованием решения задачи i(5.8.1), (5.8.2) (или, что то же самое, (5.8.4), (5.8.5)) в зависимости от параметра а. Опишем алгоритм для нахождения указанной зависимости периодических решений, который основывается на алгоритме DERPAR из § 5.2, использовавшемся для продолжения решений нелинейных (алгебраических) уравнений.

При фиксированном т1й (значение индекса k также не изменяется) соотношения (5.8.10) принимают вид

FMi.....Л*-ьЛ*+1.....Цп,Т,а) = 0, i=U2,...,n. (5.8.19)

Решение этой системы п уравнений относительно п+1 неизвестных Til, ..., Tife-i, Цк+и rin, Т, а можно исследовать с помощью алгоритма DERPAR.

Для процесса продолжения нам потребуется вычислять частные производные функций Fi по tj, Г и а. Вычисление dF,/dr]j, dFi/дТ описано в п. 5.8.2. (Непосредственно для самого процесса продолжения производные dF,/dv\k не нужны; для определения устойчивости по матрице В (5.8.17) они необходимы.) Покажем, как вычислить производную dF/da. Обозначим п = дх,/да; дифференцируя уравнение (5.8.4) по а, получим уравнения в вариациях

fr-s + -fr 2, ...,п (5.8.20)

> Речь идет о монотонности функции Xk{z).-Прим. ред.

то данный алгоритм не сработает. Поэтому в процессе продолжения мы будем адаптивно приспосабливать значение % к функции Xklz).

Рассмотрим этот вопрос более подробно. Предположим, что нам известно некоторое решение системы (5.8.19) и найдено соответствующее периодическое решение системы (5.8.4). Опишем, как выбирается значение при следующем значении а (см. рис. 5.24).

1. Возьмем монотонный участок периодического профиля > на промежутке [0,2i]U [22, 1] (где лежит значение fjj,). Через х^ (или соответственно л: ) обозначим максимум (или соответственно минимум) на этом участке. Введем следующие обозначения (О < Oi < I):

ft =Т[( + (5.8.23а)

ft = Т [(1 + 0 ft+ (1 - ft (5.8.23b)

При этом для fjft потребуем выполнения неравенства

Ч<%< (5.8.24)

Это условие означает, что % располагается достаточно далеко от локального максимума и локального минимума. Поэтому можно надеяться, что для следующего значения параметра а значение % не пропадает с профиля Xk-

2. Обозначим через Ятах максимальную разность между максимумом и минимумом на монотонном участке профиля Xkiz), если этот монотонный участок выбирать из всего промежутка [О, 1]:

Hrn.x = Xk{Z+)-Xki2-)-

Потребуем теперь, чтобы

r-r>(l~ >2)max- (5.8.25)

Это, второе условие означает, что fj лежит на достаточно широком монотонном участке.

Опыт показывает, что обычно разумно выбирать значения щ и Ш2 в диапазоне [0.5, 0.8].

Если хотя бы одно из условий (5.8.24) и (5.8.25) не выполняется, то значение % выбирается заново по формуле

овое (2+) + X, (г-)]. (5.8.26)

Остальные составляющие тц, щ-и Щ+и Л/г должны пересчитываться с использованием профилей Xi{z), Xn{z), которые были найдены для последнего значения параметра а. Для этого пересчета выберем координату г* между z- и z+ таким образом, чтобы выполнялось условие

Ч (2*) ЛГ°- (5.8.27)

Тогда значения ti?°° = лг (г ), г=1, п, будут представлять собой стартовые значения для дальнейшего процесса продолжения. При этом многошаговая схема интегрирования (например, схема Адамса-Бэшфорта), используемая в качестве предиктора в алгоритме DERPAR, вновь начинается со схемы первого порядка (т. е. схемы Эйлера). При такой организации вычислений должны также пересчитываться и некоторые управляющие параметры в алгоритме DERPAR. Прежде всего это относится к параметрам направления Л^ поскольку нам необходимо сохранять направление движения вдоль ветви периодических решений. Все детали указанного подхода читатель может найти в работе [5.17]. На рис. 5.25 схематически изображена схема описанного алгоритма нахождения периодических решений, который далее мы будем называть алгоритмом DERPER.

Отметим, что в процессе продолжения для каждого найденного периодического решения легко вычисляются его мультипликаторы. Действительно, элементы матрицы монодромии В= = (р,7(1)) получаются попутно (см. формулы (5.8.12), (5.8.17)), после чего остается лишь найти собственные значения матрицы В.

Трудности с нахождением параметрической зависимости возникают иногда в окрестности точек бифуркации (например, точки бифуркации с потерей симметрии), однако в большинстве случаев описываемый алгоритм отслеживает (гладкое) продолжение исходной ветви решений. Алгоритм беспрепятственно проходит точки рождения инвариантного тора и точки ответвления решений с двукратным периодом и прослеживает продолжение исходной ветви решений; в случае точки поворота (отвечающей бифуркации +1 (слияние двух периодических решений).- Ред.) алгоритм, пройдя эту точку, переходит на другую ветвь. Окончание ветви решений в точке бифуркации Андронова-Хопфа и в точке, где периодическое решение превращается в гомоклиническую траекторию, также контролируется этим алгоритмом (см. рис. 5.25). Проиллюстрируем использование алгоритма DERPER на нескольких примерах.

Модель Лореица {задача 10, см. (5.5.1)) обладает симметрией в следующем смысле. Введем отображение g: R-R

Корректор: предсказанные значения rj ,...,tji,1((+1 ,T,cf, корректируется с помои1,ью матода сглрельды и метода Ньютона. Полученные профили сохраняются на достаточно густой сетке j/зладых точек

Вычисление Hax-ixf , х™

Точки дифуркаи,ии Хопфа. Аонеи, семейстйа периодических решений

\рактически растет лишь Т, Г-*>-

Гомоклинная ордита-прийл.

<ыполненьг ойаусловия (5.8.24), (5.8.25)

Рис. 5.25. Схема применения алгоритма DERPER.

(симметрию относительно оси z) посредством соотношения g(x,y,z) = {-x,-y,z). Если Р (t) {x{t), у {t),z{t))--некого-