Для нахождения точки комплексной бифуркации (бифуркации Хопфа) в случае задачи 1 в § 5.5 мы вывели уравнение (5.5.15), которое в общем виде записывается как

Вф,(в, Л, Р, Y, в,) + ф2(в, Л, Р, Y, в,) = 0. (5.6.4)

Конкретный вид функций ф, и фг читатель легко может найти из формулы (5.5.15). Это уравнение вновь оказывается линей-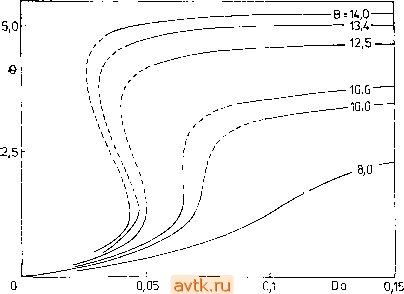

Рис. 5.18. Диаграмма стационарных решений задачи 1 для нескольких значений параметра В, у-оо, Л = 0,5, р = 0,8, вс = 0; сплошные линии - устойчивые решения, штриховые линии - неустойчивые решении.

НЫМ относительно параметра В, в связи с чем мы можем применить использованный выше подход и для построения линии нейтральности (кривой точек комплексной бифуркации). Полу-ченная кривая также изображена на бифуркационной диаграмме (рис. 5.17). Читатель может сопоставить кривую точек комплексной бифуркации и точки потери устойчивости на диаграммах решений, представленных на рис. 5.18. Далее, на рис. 5.19 изображены фазовые портреты системы двух дифференциаль- ых уравнений (Р1-6), (Р1-7) задачи 1 для нескольких выбранных значений параметров S и Da с диаграммы бифуркаций. Здесь рассмотрены следующие качественно различные случаи:

a) предельный цикл вокруг одного неустойчивого стационарного состояния;

b) предельный цикл вокруг трех неустойчивых стационарных состояний;

c) три стационарных состояния, одно из которых устойчиво, а также предельный цикл вокруг неустойчивого стационарного состояния;

Рис. 5.19. Фазовые портреты задачи 1, у-оо, р = 0,8, Л = 0,5, вс = 0. а) В= 10, Da = 0,08, b) В = 10,6, Da = 0,0653, с) S = 12,5, Da = 0,0505, d) В = 12,6, Da = 0,0475, e) В = 14, Da = 0,04; сплошная линия -траектория, штриховая линия - предельный цикл, штрихпунктирная линия -сепаратриса

d) три стационарных состояния, одно из которых устойчиво;

e) три стационарных состояния, два из которых устойчивы. Эти примеры были выбраны нами для того, чтобы читатель мог более четко уяснить зависимость между бифуркационной диаграммой, диаграммой решений и динамическим поведением системы (её фазовым портретом).

На рис. 5.20 приведены бифуркационные диаграммы для некоторых задач из гл. 4. При этом бифуркационная диаграмма для модели Лоренца {задача 10, рис. 5.20а) может быть построена аналитически.

Бифуркационная диаграмма для задачи 3 представлена на рис. 5.20Ь. Здесь изображены лишь кривые точек поворота, которые ограничивают область трех решений. Отметим, что точка возникновения изол (п. 5.4.3) отвечает крайней точке Р на кривой точек поворота. Тот же вывод можно сделать из сравнения бифуркационной диаграммы с геометрической схемой, изображенной на рис. 5.10.

На рис. 5.20с приведена бифуркационная диаграмма для задачи 2. На ней изображены лишь кривые комплексной бифуркации (бифуркации Хопфа), причем стационарное решение остается единственным во всей плоскости параметров Dai-Ваг. Выделенные точки на бифуркационной диаграмме соответствуют точкам бифуркации Хопфа, вычисленным в § 5.5 (см. также табл. 5.13). При этом стационарное решение оказывается устойчивым в областях II и IV и, наоборот, неустойчивым в областях I и III, в которых, как мы увидим в § 5.8, существуют устойчивые периодические решения (предельные циклы).

На рис. 5.20d изображена бифуркационная диаграмма для задачи 6. Кривую точек поворота (линию кратности) можно вновь построить с помощью метода отображения параметра, как это сделано для рис. 5.17. Указанная кривая ограничивает область возникновения трех стационарных решений; вне этой области существует одно стационарное решение.

Бифуркационная диаграмма для задачи 4 представлена на рис. 5.20е в плоскости параметров б - а. В области, ограниченной кривыми вещественных бифуркаций, существует три решения, вне этой области -одно решение. Кривые комплексной бифуркации указывают нам на ответвление периодических решений и изменение характера устойчивости стационарных решений. В области единственности стационарных решений эти кривые выделяют область существования устойчивых предельных циклов.

На рис. 5.20f изображена бифуркационная диаграмма для задачи 8 в плоскости параметров B - Du Ввиду симметрии системы некоторые кривые являются фактически сдвоенными, поскольку бифуркация возникает одновременно у двух взаимно симметричных решений при тех же самых значениях параметров (сравните с диаграммой решений на рис. 5.6d). Для каждой области на бифуркационной диаграмме указано общее число стационарных решений.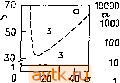

0,3 0,2

0,1 h 0

о 0,1 0,2 р^0,3

0,001 011 0,1 1 10 рЮО 100D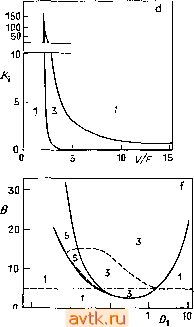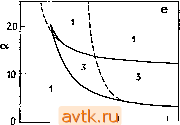

0,001 0,01 0,1

0,02 0,0Б рд0,1

Рис. 5.20. Бифуркационные диаграммы для отдельных задач; сплошная линия - кривая предельных точек, штриховая линия - кривая точек комплексной бифуркации (бифуркации Андронова - Хопфа). Числа в отдельных областях указывают число стационарных решений, а) задача 10, 6 = 4. Ь) Задача 3, l = 8,410- = 2, 8 = 6,6667-10-, е'= 1,7778-10-=. Точки Р и Q -см. рис. 5.10 и 5.12. с) Задача 2, у = 1000, В = 12, Pj = Pj = 2, в^ = = = О, Л = 1. d) Задача 6, cq = 5, cq = 0,005, S = 0,5, = 0,03, ji= = 0,5. е) Зааача 4, Y = 3, Р= 1,5. = О, 01. f) Задача 8, N = 2, уравнения (Р8-2)-(Р8-5), Л=2, £)2=10£>1, штрихпунктирная линия-кривая точек бифуркации Андронова - Хопфа на ветви неустойчивых стационарных решений, g) Задача у = 20, 6, = в^ = ~ 5, Л = 1, В = 10, р, = р^ = 0,2.

Более сложная бифуркационная диаграмма имеет место для задачи 2 (рис. 5.20g). Здесь также в каждой области параметрической плоскости Dai - Da2 указано общее число стационарных решений.

В случае более сложных задач основная проблема заключается в том, чтобы простроить полную бифуркационную диаграмму, т. е. найти ее кривые точек поворота и точек комплексной бифуркации. Если мы сумеем построить такую диаграмму, то тем самым получим полную информацию о поведении стационарных решений системы в зависимости от двух параметров исходной задачи.

5.7. МЕТОДЫ МОДЕЛИРОВАНИЯ ДИНАМИЧЕСКИХ СИСТЕМ

Решение x{t) системы обыкновенных дифференциальных уравнений

=-nt, X) (5.7.1)

с начальным условием х(0) = х' (за редкими исключениями, когда нам удается решить уравнение (5.7.1) аналитически) обычно приходится находить численными методами. За последние 40 лет разработан целый ряд таких методов, позволяющих строить решения задач Коши для обыкновенных дифференциальных уравнений, и в настоящее время соответствующие программы являются частью математического обеспечения практически любой ЭВМ.

Подчеркнем, что некритическое использование этих программ может в некоторых задачах приводить к неправильным результатам (или вовсе не приводить к результатам). Это может случиться, в частности, при интегрировании систем с сильно неустойчивыми траекториями или систем, содержащих малые параметры.

В этом параграфе будет приведен лишь краткий обзор указанных методов и рассмотрены некоторые практические аспекты их использования. Читателей, которых данная проблематика заинтересует более глубоко, мы отсылаем к обширной библиографии по этому вопросу (см., например, [5.7], [16*], [18*], [19*]).

5.7.1. Одношаговые методы

Общая особенность численных методов решения задачи Коши (или методов численного интегрирования) состоит в том, что решение ищется в виде некоторой дискретно определенной

функции, заданной на сетке, состоящей из узлов to = О, /2, ... с шагом hj = tj+i - tj > 0. Методы интегрирования можно разделить на две группы: одношаговые и многошаговые.

В одношаговых методах для нахождения приближенного решения в точке tj+i используется аппроксимация решения лишь в одной предшествующей узловой точке t/, т. е.

хЖ = х' + Л/Ф(0, х'. Л/). (5.7.2)

Вид функции Ф зависит от конкретного задания правых частей дифференциальных уравнений (5.7.1) и от выбранного метода. Начиная с х' = х(0) при вычислениях можно использовать рекуррентную процедуру (5.7.2), продвигаясь шаг за шагом по оси t. Для так называемых неявных методов функция Ф зависит также от вектора х'+, так что алгоритм перехода от tf к tj+i должен включать в себя какую-либо итерационную процедуру для решения системы нелинейных уравнений, относительно компонент х'+.

5.7.1.1. Методы с использованием разложения Тейлора

Эти методы используются лишь в случаях, когда правые части уравнений (5.7.1) можно легко продифференцировать аналитически и когда размерность системы не слишком велика. Соотношение (5.7.2) при этом принимает вид

Х/+1 = x + h, (х') + (х') + If Ы) + + (х') , (5.7.3)

где использовано обозначение (х^)= f ((/, х'), а последующие производные получаются путем дифференцирования уравнений (5.7.1) по переменной t и последующей подстановки значений tj, X. Так, для (х'У имеем

, di(t х') df(ti, х') , , ,

Дальнейшее дифференцирование для конкретного вида уравнений читатель может проделать самостоятельно. Очевидно, что для сложных правых частей, а также в случае системы больших размеров такие вычисления могут оказаться громоздкими и весьма трудоемкими.

Если обозначить через x(t) точное решение дифференциальных уравнений (5.7.1), удовлетворяющее начальному условию х(/) = х', то значение x(/+i) будет отличаться от х'+, найденного по формуле (5.7.3), на остаточный член тейлоровского

(p + i)l

Эта разность называется погрешностью аппроксимации на одном шаге, или, иначе, локальной погрешностью аппроксимации. Обозначим теперь через \{t) решение уравнения (5.7.1), удовлетворяющее условию х(о) = х°. Тогда глобальной погрешностью аппроксимации при фиксированном = ? мы называем выражение

£ = ttx-x(OII, (5.7.4)

где / = (i - to)/h. Если при /i->-0 локальная погрешность аппроксимации есть 0{hP+), то глобальная погрешность аппроксимации имеет порядок малости на 1 меньше (E = 0(h)). В связи с этим схема (5.7.3) называется схемой р-го порядка. Ниже для всех численных схем мы будем указывать только порядок глобальной погрешности аппроксимации для h = const.

5.7.1.2. Варианты метода Рунге - Кутты

Наиболее распространенными из всех являются различные варианты метода Рунге - Кутты. При этом функция Ф в соотношении (5.7.2) задается с помощью расчетной схемы

Х/+1 = X -f Yiki + Y2k2 + ... + Ym+.k +.. (5.7.5)

где векторы к,- вычисляются рекуррентно по формулам

к, = ( , х'),

к2 = М( + а,Л, x + Puki).

кз = М {ti -f аА х' + Paiki + Разкг), (5.7.6)

k,n+i = h.i {tj + a h, х' + pik, + ... + ттЮ-

Для наглядности сопоставим соотношениям (5.7.5), (5.7.6) следующую схему:

(5.7.7)

разложения, т. е. на член вида (Л/ = h)

Таблица 5.18. Варианты метода Рунге-Кутты а) усовершенствованный метод Эйлера, O(ft)

b) модифицированный метод Эйлера, 0(№)

с) метод Хюна, 0(h?)

d) метод Кутты, 0(h)

е) стандартный вариант метода, О (Л*)

g) метод Нюстрёма, 0(№)

В табл. 5.18 представлены схемы различных вариантов метода Рунге - Кутты, соответствующие разным значениям коэффициентов а, р и 7. Для каждого из них указывается также порядок погрешности аппроксимации (см. п. 5.7.1.1). Наиболее простым вариантом метода Рунге - Кутты является метод Эйлера

x/+i = x/-f М(/,-, хО, (5.7.8)

имеющий первый порядок точности (одновременно он является методом, основанным на разложении Тейлора). Чтобы получить у метода Рунге - Кутты порядок погрешности 0(/ip) для р = \, 2, 3, 4, необходимо выполнить соответственно 1, 2, 3, 4 подстановки в правую часть решаемого дифференциального уравнения. При р = 5 требуется уже минимум шесть подстановок; вообще говоря, для р > 4 всегда оказывается необходимым использовать больше чем р подстановок. Методы, имеющие порядок погрешности больше 4, используются поэтому достаточно редко - их преимущества проявляются лишь при высоких требованиях к точности вычислений.

5.7.1.3. Апостериорная оценка погрешности аппроксимации

При численном решении нам всегда нужно выяснить, с какой точностью мы нашли решение исследуемой задачи. В большинстве численных методов для оценки погрешностей аппроксимации получены соотношения, основанные на использовании производных высших порядков от решения и правых частей на всем исследуемом промежутке. Однако эти так называемые априорные оценки погрешностей аппроксимации часто получаются чересчур пессимистичными: фактическая погрешность аппроксимации оказывается существенно меньше оценки. Вдобавок они требуют громоздких вычислений. Поэтому в подавляющем большинстве случаев используются апостериорные (т. е. осуществляемые после проведения вычислений) оценки погреш-

lim ±i = CO.

Более точно, предположим, что

£(A) = C/i-f 0(/i+). (5.7.9)

Здесь член 0(hp+) убывает быстрее, чем предыдущий, и при достаточно малых h мы можем им пренебречь. Подсчитаем две различных аппроксимации решения Qi и Q2 (при одном t) для двух различных шагов hi и /12, полагая, например, hi/h2 = 2 (Qs здесь играют роль переменной х' в (5.7.4), однако для различных шагов индекс / также будет различным). Обозначим через Q точное решение задачи. Для вычислений с шагом hi мы имеем

Qi Q-faf, (5.7.10)

а в случае шага Лг

Q2>Q + Chl (5.7.11)

Если рассматривать уравнения (5.7.10) и (5.7.11) как точные, то они составляют систему двух линейных алгебраических уравнений относительно неизвестных Q и С. Значение Q, найденное из этой системы, обозначим Q12:

Величина Q12 не равна в точности Q, поскольку мы пренебрегли слагаемым 0(/iP+) в формуле (5.7.9). Соотношение (5.7.12) и связанный с ним подход называются экстраполяцией Ричардсона и используются для апостериорной оценки погрешности аппроксимации:

£i = IIQ.-Qi2ll, £2 = IIQ2-Qi2ll. (5.7.13)

ностей. Для решения задачи Коши х(/) при фиксированном t (см. формулу (5.7.4)) погрешность аппроксимации зависит от:

а) характера исследуемой задачи (вида дифференциальных уравнений, начальных условий и т. д.),

б) применяемого метода и его порядка,

в) используемого шага h - в данном случае мы считаем его постоянным.

Если же мы фиксировали задачу и метод расчета, то в таком случае погрешность аппроксимации решения (при фиксированном t) зависит только от величины шага h. Предположим, что

EJh)