

 |
 |
|
Разделы
Публикации
Популярные
Новые
|
Главная » Квазистационарное поведение динамических моделей 1 ... 14 15 16 17 18 19 20 ... 36 1071   Рис. 5.10. Возникновение изол в двухпараметрической проекции.  <2 > Л2 <<1 Я*ис. 5.11. Схематическое изображение возиикиовеиия изол иа диаграмме решений. J*-s = -. (5.4.38> дх. ( да \ I или -- I *> Компоненты г имеют смысл производных \ или - на по- верхности f = 0. Однако систему (5.4.35) можно рассматривать н вне этой; поверхности; тогда г = г(х, ai, 2). Именно так понимается Гп в (5.4.37).- Прим. ред. как функцию переменных Xk, oci (прн некотором фиксированном k) a2 = (p(Xk, щ). (5.4.33) Действительно, выбрав значения Xk н аь нз уравнений (5.4.32) можно определить оставшиеся неизвестные xi, .... Xk-i, Xk+i, .... ..., Хп н а2 V. таким образом получить функциональные зависимости Xj = XjiXk,oci) н (Х2 = a2{xk, oci) {=(f){xk,cici)). Функция ф имеет экстремум в точке Р и, следовательно, для нее должны выполняться соотношения Положим Хп+1 = 2, считая, что матрица задана выражением (5.2.12). Дифференцируя систему (5.4.32) по переменной Xk, мы получаем систему линейных алгебраических уравнений h-T = -- (5.4.35> относительно составляющих вектора \.дх..... дх дх дх dxj- (5.4.36) Первое нз условий (5.4.34) можно прн этом записать в виде r {xi, Х2, х„, щ, 02) = О (5.4.37) Дифференцируя (5.4.32) по аь получим систему где использовано обозначение дх, дх. , дх , дх да\ ~Ч(Эа,5а, За, 5а, daJ (5.4.39> и, следовательно, второе нз условий (5.4.34) записывается в виде Snixi, Х2, х„, щ, 02) = 0. (5.4.40) дх% дх% да\ So, (5.4.41) то функция ф имеет минимум и, следовательно, изолы существуют при > а^. Если же первое из неравенств (5.4.41) имеет обратный знак, то изолы существуют при Og < а^. Рассмотрим пример использования описанного выше алгоритма для нахождения точки возникновения изол. Обратимся вновь к задаче 1 в формулировке с использованием времени задержки т, которое в данном случае играет роль параметра аь Обращаясь к рис. 5.2, мы видим, что критическое значение параметра а (выступающего здесь в роли параметра аг) приблизительно равно 5. Воспользуемся соотношением (5.2.3). Стационарные состояния при этом описываются уравнением (5.2.4). > Имеется в виду решение системы f(x, ai, аг) = О при фиксированных ai и аг. - Прим.. ред. Отметим, ЧТО системы (5.4.35) и (5.4.38) имеют одну и ту же матрицу и, следовательно, решение их может быть найдено с помощью метода исключения Гаусса для обеих правых частей одновременно. Итак, для определения координат точки Р мы имеем в самом общем случае п + 2 уравнений (5.4.32), (5.4.37) и (5.4.40) относительно п + 2 неизвестных Xi,X2.....д; , ai, аг [5.13]. Задавая значения этих неизвестных, мы можем найти левые части указанных п + 2 уравнений и затем использовать для нахождения решений этой системы соответствующие итерационные процедуры, например обобщенный метод секущих или метод Ньютона с матрицей Якоби, подсчитываемой с помощью разностных формул (при аналитическом вычислении производных для соотношений (5.4.37) и (5.4.40) нам потребовалось бы вычислять частные производные второго порядка от функций /,). Изолы могут существовать либо при > о,, либо при < < Og. Различить между собой эти два случая можно опытным путем, используя метод Ньютона для Og > и Og < al, причем существование решения доказывается сходимостью к этому решению на изолеДругая возможность заключается в том, чтобы вычислить частные производные второго порядка д\1дх\, d9/dXj.da д\1да\ и использовать условия Сильвестра для минимума и максимума функции (p{Xk,a). Так, если Используя формулы Da = kox, р = ах, имеем из (5.2.4) /,(в, т, fl) = -Ae + v(fi-e- °(е-е^))х Хехр J в + e/Y -ат(в-0с)=О. (5.4.42) Поскольку п=1, мы получаем Xk = xi=e. Уравнение (5.4.35) принимает вид (5.4.43) да дв и, следовательно, соотношение (5.4.37) эквивалентно условию dfi . , Г /, , ат Л , / г. ат (в - 9с) л 1 .=-A+[-(.+)+(fl-e-ii2e2i) дв L V Л У Л л J (1+в/у)Ч' XA:oTexp-j-j-aT = 0. (5.4.44) Аналогичным образом, уравнение (5.4.38) записывается в виде Eh. да а условие (5.4.40) дает 2ах (в - вс) Л ехр в l+e/Y (5.4.45) -a(0-Gc) = O. (5.4.46) Таким образом, мы имеем три уравнения (5.4.42), (5.4.44) и (5.4.46) для трех неизвестных в, т и а. Ход итераций, полученных при использовании метода Ньютона с матрицей Якоби, которая вычислялась с помощью соответствующих разностных формул, представлен в табл. 5.10. Полученные результаты соответствуют диаграмме решений, изображенной на рис. 5.2. Таблица 5.10. Расчет точки возникновения изол для задачи 1. (Метод Ньютона для системы уравнений (5.4.42), (5.4.44) и (5.4.46); v = 20, В= 10, Л= 1, в, - -5, ко -- 1).
В работе [5.13] был рассмотрен еще один алгоритм для определения точки возникновения изол. Так, на зависимости - = 20 ----- . 280 1000 -----ot = 800 - - л =2000 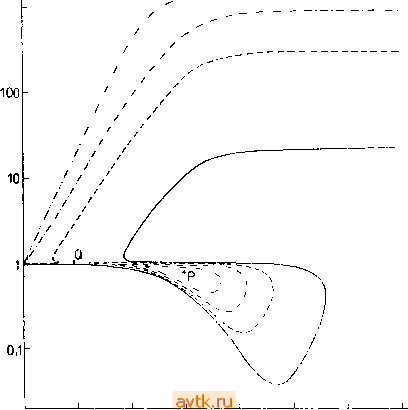 0,001 0,01 0,1 1 10 100 1000 10000 Рис. 5.12. Диаграмма стационарных решений задачи 3; ц = 8,4-10-, f = 2, е = 6,6667-10- е'= ],7778-10-1 Точка Р -см. рнс. 5.10, точки Р н Q - см. рис. 5.206. х(а2) При а, = 0* точка Р представляет собой точку поворота (см. также рис. 5.10). Необходимое условие для точки Р имс?т , a2)==detJCxi, Хп, аь 02)== О, (5.4.47) при этом вид /п + 1 (-Ь > Х„, Щ где J = [dfi/dxf] - матрица Якоби. При фиксированном х^ = х1 зависимость (xi.....Xk-i, Xk+i, x ,ai) от 2 также имеет точку поворота, и поэтому должно быть выполнено условие fn+iixi, аь a2) = det4(д;ь х^, щ, а2) = 0, (5.4.48) где матрица определяется по формуле (5.2.12) при Xn+i = ь Объединив (5.4.32), (5.4.47) и (5.4.48), мы вновь получаем п-\-2 нелинейных уравнений относительно п-\-2 неизвестных. Отметим, что уравнения (5.4.47) и (5.4.48) формально тождественны соотношениям (5.4.1) и (5.4.2) для нахождения точек ветвления. Однако здесь мы имеем на одну переменную больше (добавится аг), и для решения этой системы мы используем метод Ньютона (в отличие от п. 5.4.1, где применялся метод Гаусса - Ньютона). Читатель, который воспользуется вторым методом для нахождения точек возникновения изол в уравнении (5.4.42), получит те же результаты, что и в случае применения первого метода, поскольку здесь п = 1. Применим оба описанных подхода для анализа задачи 3, где роль параметра ai будет играть параметр р, а роль параметра аг - параметр а. Пример расчета итераций по методу Ньютона (матрица Якоби вычисляется с помощью соответ- Таблица 5.11. Расчет точек возникновения изол в задаче 3 (fi, = 8,4 X Ю , f = 2, 8 = 6,6667X 10-, е'= 1,7778 X 10-5). Ход итераций по методу Ньютона.
Этот термин не является общепринятым. - Яриж. ред. > Корни многочлена третьей степени легко находятся, если среди них сть чисто мнимые. ствующих разностных формул) приведен в табл. 5.11. Соответствующая диаграмма решений для различных значений параметра а изображена на рис. 5.12. 5.5. КОМПЛЕКСНАЯ БИФУРКАЦИЯ (БИФУРКАЦИЯ ХОПФА) 1 1 Устойчивость стационарного решения системы (5.1.1) характеризуется собственными числами матрицы Якоби, определяемой правыми частями соответствующих уравнений. Если мы изменяем один из параметров системы, то вдоль ветви решения на соответствующей диаграмме решений характер устойчивости может изменяться лишь в точках, где собственное число переходит из левой половины комплексной плоскости в правую. Переход вещественного собственного числа через нуль обсуждался нами в § 5.2. Если пара комплексно-сопряженных собственных чисел пересекает мнимую ось, то матрица Якоби все время остается невырожденной, и на диаграмме стационарных решений мы имеем регулярную точку данной ветви. Однако характер стационарного решения при этом переходе может измениться: устойчивое решение может стать неустойчивым (или наоборот). Точки диаграммы стационарных решений, в которых пара комплексно-сопряженных собственных чисел пересекает мнимую ось, называются точками комплексной бифуркации или точками бифуркации Хопфа, по имени математика, опубликовавшего одну из основополагающих работ о характере решений в окрестности таких точек. Следующий существенный факт мотивирует разработку алгоритмов для нахождения точек комплексной бифуркации: в указанных точках (при выполнении определенных условий) от ветви стационарных решений отходит ветвь периодических решений. Этот параграф мы посвятим методам определения этих точек; алгоритмам для расчета и продолжения периодических решений будет посвящен §5.8. 5.5.1. Аналитические подходы В случае некоторых задач невысокой размерности для нахождения точек комплексной бифуркации нет необходимости обращаться к численным методам. Можно воспользоваться аналитическими подходами, основанными на том, что мы легко раскрываем определители матриц порядка 2 и 3 и находим корни многочленов такой же степени 2). Если вещественный многочлен + А^Х^ + АЛ + Ао имеет чнсто мнимый корень, то Ао = ЛИг. - Прим. ред. Проиллюстрируем сказанное на примере двух задач: моделю Лоренца (см. задачу 10) и модели реактора с перемешиванием, для реакции 1-го порядка (см. задачу 1). Модель Лоренца описывается системой уравнений X = -cfx + (Уу, у =-XZгх - у, (5.5.1> z = xy~ bz, правые части которых имеют матрицу Якоби вида -or or О' J= r-z -1 -д; . (5.5.2> . у X -Ь. Для нетривиального стационарного решения (см. формулу (Р10-5)) х = у = ±[Ь{г-\)] \ z = r-l, г>1 (5.5.3> построим характеристический многочлен матрицы J Р(Я) = ЯЗ + (ог + й+ 1)Я2 + й(г + ог)Я + 2огй(г- 1). (5.5.4) В точке бифуркации Хопфа этот многочлен должен иметь два взаимно сопряженных чисто мнимых корня, которые мы обозначим как dzJXo. Третий (вещественный) корень обозначим Xi. Тогда Р (Я) = (Я + гЯр) (Я - i\) (Я - Я,) = ЯЗ - Я,Я2 + Я^Я - (5.5.5> Сравнивая формулы (5.5.4) и (5.5.5), получим а + й-Ы = -Я„ й(г + ог) = Я2, (5.5.6> 2ай(г- 1) = -Я,Я2. Считая or и й фиксированными, имеем систему трех уравнений относительно неизвестных Яо, Я] и г. Если учесть, что г > 1, то-из уравнений (5.5.6) следует, что Xi < О и коФО. Перемножая левые и правые части первых двух уравнений системы (5.5.6) и вычитая полученный результат из последнего уравнения-(5.5.6), мы получаем соотношение (а + й+1)й(г + а) = 2огй(г-1). (5.5.8) L 21 22 j характеристический многочлен J имеет вид Р {%) = Я2 - (а,1 + 022) + (11022 - 2112). (5.5.9) в точке комплексной бифуркации этот многочлен имеет два чисто мнимых корня: Р (Я) = (%- а„) (Я + i\) = Я2 + XI. (5.5.10) Сравнение (5.5.9) и (5.5.10) дает 11 + 22 = О, ; (5.5.11) aua-n - a2\ai2 = Xo>0. Используем теперь описанный подход для отыскания точек комплексной бифуркации в задаче 1. Матрица Якоби для правых частей уравнений (Р1-6) и (Р1-7) имеет вид -Л-Оа£(в) Т>а{\-x)Ex{Q) L-Da5£(e) -Л + 0аБ(1-a:)£i(G)-PJ (5.5.12) где введены обозначения £ (6) = ехр(6/(1 + в/у)) и £1(6) = = £(6)/(l + 6/Y)2. Первое из условий (5.5.11) приводит нас к уравнению -2Л - Da £ (0) + Da (б - 6 - -- (6 - 6,)) £, (6) - Р = О, (5.5.13) где мы подставили л: = 6/В + р(6 - 6с)/ВЛ (см. формулу 5.2.3)). Уравнения, описывающие стационарное состояние, .дают еще соотношение между 6 и Da (см. (5.4.16): вш в!ч- (5.5.14) В которое ВХОДИТ только неизвестная г. Отсюда г - (а - й - 1) где г+ -значение параметра г в точке комплексной бифуркации; значения переменных д;+, г/+, 2+ подсчитываются по формулам (5.5.3). Для системы двух дифференциальных уравнений с матрицей Якоби Подставляя выражение для Da в уравнение (5.5.13), мы получаем кубическое уравнение относительно в (при фиксированных В, Л, р, вс) следующего вида: (р(в-вс)-ьлв-(2л-ьр)(1+в/у)2) (д-е- P(Q-Q)) - (р(в-0,)-ЬЛв)(1-Ь0/у)2 = о. (5.5.15) Решение этого уравнения дает нам значения переменной в+, после чего по формуле (5.5.14) нетрудно найти значения параметра Da+, отвечающие точке комплексной бифуркации. В табл. 5.12 приведен пример такого расчета для двух значений параметра В в предельном случае у^оо (когда (5.5.15) сводится к квадратному уравнению). Таблица 5.12. Нахождение точек комплексной бифуркации для задачи 1 (у-оо, Л = 0,5, р = 0,8, вс = 0).
В приведенных примерах мы определяли точки бифуркации Хопфа для задач, размерность которых не превышала 3. Для задач, описываемых системами более чем из 3 дифференциальных уравнений, исследователям приходится обычно использовать различного рода численные подходы. Часть из них будет рассмотрена в следующих двух пунктах [5.14, 5.15, 5.16]. 5.5.2. Методы декомпозиции В точке комплексной бифуркации (бифуркации Хопфа) (xj* , х+, а+) матрица Якоби J имеет два (взаимно) сопряженных чисто мнимых собственных числа Xi и Яг, т. е. X 2=±fV , сй+>0. (5.5.16) Запишем характеристический многочлен матрицы J, Р(Я) = Г-Ьа,Г-Ч ... +а^ ,Х + а^, (5.5.17) и представим его в виде />(Я) = (Я2-Ьсй+)Р„ 2(Я), (5.5.18) 1 ... 14 15 16 17 18 19 20 ... 36 |
|
© 2004-2025 AVTK.RU. Поддержка сайта: +7 495 7950139 в тональном режиме 271761
Копирование материалов разрешено при условии активной ссылки. |