где Р„ 2(Я)-многочлен степени п - 2. Для нахождения величины CU+ (заранее неизвестной) перепишем Р(к) в форме

Р{к) = {х' + а>){х - + рХ~+ ... +Рп-г^ + Рп-2) + Ак + В.

Коэффициенты pi, ..., рп, А и В могут быть вычислены по рекуррентным формулам

Р-1 = 0, Ро=1, Pk = k~Pk-2 k=l, 2, .. ., п - 2

л d (5.5.19)

А = а„ , - сйр„ з, В = а„- ©р„ 2.

Величины pi, А и В зависят от х, а и со. При этом для точки комплексной бифуркации выполняются соотношения

fn+i{xi, х„, а, сй) = Л(д;1, х^, а, а>) = 0, fn+2{Xu х^, а, (i>)=B{Xi, Хп, а, сй)==0.

Таким образом, в общем случае мы имеем (п + 2) нелинейных уравнений (5.1.3), (5.5.20) относительно (п + 2) неизвестных Xl, Хп, а, со. Решение этих уравнений позволяет нам найти точку комплексной бифуркации. Для нахождения решения можно воспользоваться методом Ньютона, а для вычисления элементов матрицы Якоби в методе Ньютона можно частично (для нахождения производных от fn+i и fn+2) использовать разностные формулы. Можно использовать и аналитические выражения, однако в случае больших п это может оказаться весьма трудоемким.

Отметим, что коэффициенты pi.....р„ 2 несут информацию

об устойчивости стационарного решения в окрестности точки комплексной бифуркации (бифуркации Хопфа). Если все корни многочлена с указанными коэффициентами располагаются в левой полуплоскости (см. § 5.3), то стационарное решение будет устойчивым либо при а < а+, либо при а > а+.

Примеры применения описанного метода для трех различных точек комплексной бифуркации в случае задачи 2 представлены в табл. 5.13. При этом в качестве параметра а использовалось число Дамкёлера в первом реакторе каскада Daj.

Если матрица J имеет собственное число К, то матрица обладает собственным числом Я^. Для собственных чисел (5.5.16) мы имеем к\ 2 = -(й'. Итак, матрица имеет отрицательное вещественное собственное число -сй+ кратности два. Обозначим характеристический многочлен матрицы через Q(©). Тогда в точке бифуркации Хопфа имеют место условия

Таблица 5.13. Сходимость метода Ньютона для системы (5.1.3), (5.5.20) к точкам бифуркации Хопфа в случае задачи 2 (у = 1000 В - 12 Р, = Рг = 2, вс, = в„ = О, Л = 0,8, Daj = 0,2, а - Da,)

Q(-cu+) = 0, Q(-cu+) = 0. Соотношения (5.5.20) заменяются лри этом соотношениями

f +i(-Kb -v , а, cu) = Q((u) = 0,

frt+2 (-l,

a, Cu) =

rfQ (CO)

(5.5.21)

Систему (x, a, a) = 0 (/= 1, ..., n + 2; см. (5.1.3) и (5.5.21)) можно решать методом Ньютона. Если этот метод дает сходимость к точке (х+ а+, -CU+), где (0+< О, то она не является точкой бифуркации Хопфа, поскольку тогда матрица J имеет два вещественных собственных числа

5.5.3. Прямые итерационные процедуры

Описываемые здесь методы не требуют вычисления характеристического многочлена, как в предыдущем пункте.

Пусть U - собственный вектор матрицы Якоби J, соответствующий собственному числу Я:

Ju = A,u. (5.5.22)

В точке комплексной бифуркации мы имеем К = is, s е R и u = v + iw, где V и w - вещественные векторы. Разделяя в (5.5.22) вещественные и мнимые части, получаем

Jv + SW = О, (5.5.23)

Jw - SV = 0. (5.5.24)

Запишем теперь уравнения ,(5.5.23) и (5.5.24) покомпонентно в виде

fi (xi.....x , а, s, Vi, u , Wi, ..., да ) = 0,

i = n+ 1, n + 2, 3tt, (5.5.25)

где j = 1, 2, ..., П, -правые части исходной системы (5.1.1).

Произведение вектора и на произвольное комплексное число также является собственным вектором матрицы J, соответствую-

Рис. 5.13. Матрица размещения для уравнений (5.1.3), (5.5.23), (5.5.24).

щим собственному числу К = is. Это означает, что, вообще говоря, мы можем выбрать произвольно две составляющих векторов V и W. Мы не будем обсуждать здесь условия успешности подобного выбора. Так, могут иметь место ситуации, когда этот выбор окажется неудачным, однако при случайном выборе это маловероятно.

Система уравнений (5.1.3) и (5.5.25) представляет собой систему Зп нелинейных уравнений относительно (Зп + 2) неизвестных {Xi,X2, Хп, а, S, Vu V2, Vn, Wi, W2, Wn). Из

последних 2n неизвестных мы, однако, считаем две переменных фиксированными, в результате чего у нас получается система Зп уравнений относительно Зп неизвестных, решение которой можно вновь строить с помощью метода Ньютона. Часть элементов матрицы Якоби нетрудно найти аналитически, а оставшиеся элементы определить, аппроксимируя частные производные конечными разностями. Таблица вхождения переменных в уравнения решаемой системы представлена на рис. 5.13. Она определяет также отличные от нуля элементы матрицы Якоби (порядка Зп). Те из них, которые можно определить

аналитически обозначены на рисунке кружком. С учетом выбора двух компонент векторов v и w (которые остаются фиксированными в ходе итераций по методу Ньютона), векторы v и w могут иметь размерность в соответствии с одним из следующих трех вариантов:

1. dimv = n -2, dimw = n, фиксированы 2 компоненты

вектора v.

2. dimv = n-1, dimw = n-1, фиксированы по одной ком-

поненте векторов V и W.

3. dim v = п, dim w = п - 2, фиксированы 2 компоненты

вектора w.

Пример сходимости метода Ньютона при решении системы уравнений (5.1.3), (5.5.23), (5.5.24) приведен в табл. 5.14. В таблице указано, какие две компоненты векторов v и w выбирались фиксированными. Предлагаем читателю сравнить найденную точку комплексной бифуркации с результатами, представленными в табл. 5.13.

Еще один метод, который мы здесь рассмотрим, основан на аналогичном принципе, однако размерность решаемой нелинейной системы оказывается более низкой (2п вместо Зп).

Из уравнений (5.5.23) и (5.5.24) легко находим

J2v + sv = 0. (5.5.26)

Запишем (5.5.26) в виде

fiixu . .., Хп, а, со, Ui, . . ., и„) = 0, г = п+ 1, . .., 2п,

(5.5.27)

где использовано обозначение a = s. Таким образом, мы имеем систему 2п нелинейных уравнений (5.1.3), (5.5.27) относительно 2п-1-2 неизвестных хи Хп, а, со, Vu и„. В векторе v мы снова можем произвольно задать две его составляющие. На рис. 5.14 представлена таблица вхождения неизвестных для решаемой системы. Элементы матрицы Якоби (порядка 2п), которые можно легко найти аналитически, обозначены кружками. Характер сходимости метода Ньютона хорошо виден из табл. 5.15.

В заключение параграфа сравним особенности методов, описанных в пп. 5.5.2 и 5.5.3. Так, если сравнивать ограничения а объем памяти и число операций для каждого из этих мето-

В предположении, что производные правых частей исходной системы шо X, и а находятся аналитически. - Прим. ред.

Таблица 5.14. Сходимость метода Ньютона к точке бифуркации для системы (5.1.3), (5.5.23), (5.5.24) в случае задачи 2 (у = 1000, В = 12, Pi = Рг = 2, вн = 9,2 = О, Л = 0,8, Оаг - 0,2, а = Da,).

Номер итерации

/ 12 \ 1/2

0 0,5000 1,0000 0,7000 1,9000 0,1000 0,7000 1,0000 1,0000 1,0000 1,0000 1,0000 1,0000 1,0000 1.0000 1,2 Е1

1 0,3531 0,9915 0,6149 1,0634 0,1410 0,7346 4,5930 11,7247 0,2824 3,4724 3,1896 33,0158 3,0 Е1

2 0,2917 0,7728 0,6178 1,5015 0,1139 0,6250 3,9275 8,2677 0,4104 3,2657 3,0732 26,8698 5,6 ЕО

3 0,2713 0,6701 0,6696 1,8082 0,0980 0,6619 3,8409 6,8199 0,4261 3,3781 3,5048 30,7556 9,6 Е-1

4 0,2714 0,6658 0,6793 1,8533 0,0957 0,6710 I i 3,7973 6,4110 0,4341 3,4675 3,5808 32,0305 4,0 Е-2

5 0,2712 0,6651 0,6794 1,8543 0,0956 0,6702 1,0000 1,0000 3,7990 6,4239 0,4339 3,4648 3,5813 32,0553 9,0 Е-6

О 0,40000 1,0000 0,7000 1,8000 0,1000 0,5000 1,0000 1,0000 1,0000 1,0000 1,0000 1,0000 1,0000 1,0000 1,1 Е1 8 0,2712 0,6651 0,6794 1,8543 0,0956 0,6702 1,0000 1,0000 3,7990 6,4239 0,4339 3,4648 3,5813 32,0553 6,2 Е-6

Таблица 5.15. Сходимость метода Ньютона при определении точки бифуркации Хопфа из системы (5.1.3), (5.5.27) в задаче 2 (у = 1000, В = 12, &ci = вс2 = О, Pi = Рг = 2, Л = 0,8, Оаг = 0,2, а = Da,).

дов (приведены только главные члены в оцениваемых величинах), то из данных табл. 5.16 следует, что метод, основанный на решении системы (5.1.3), (5.5.23), (5.5.24), оказывается более предпочтительным для тех ЭВМ, у которых объем памяти достаточно велик.

Дальнейшие выводы мы можем сделать из рассмотрения данных табл. 5.17. Исходные значения всех переменных формировались случайным образом (с помощью генератора случайных чисел) из следующих промежутков: Хь лгг е(0, 1), вь ©2(0,4), ае(0, 1), se(0, 10), Vi, ш,-е(-20, 20), где = со.

Рис. 5.14. Матрица размещения для уравнений (5.1.3), (5.5.26), dimvn - 2.

Случайно выбирались также индексы и величины составляющих векторов V и W, которые остаются фиксированными в ходе решения. Выбранные исходные значения для каждого из четырех рассмотренных методов использовались в качестве начальной аппроксимации для метода Ньютона. При этом оказалось, что с точки зрения сходимости наихудшие результаты дает метод с использованием уравнений (5.1.3), (5.5.21).

Таблица 5.16. Скорость роста объема памяти и числа операций при увеличении п для разных методов отыскания точки комплексной бифуркации.

Таблица 5.17. Эффективность различных методов для задачи 2. Здесь же указано число начальных приближений (из общего числа 1000 приближений, выбранных случайным образом), при которых метод Ньютона сходится к какому-либо из трех решений. Значения параметров: у = 1000, В = 12, Pi = Рз = 2, вс1 = вс2 = О, Л = 0,8, Dai = 0,2, а = Dai.

Методы, рассмотренные в данном пункте, легко обобщаются на случай нахождения точек комплексной бифуркации для дифференциальных уравнений с частными производными параболического типа. Это обобщение будет проведено в гл. 6.

5.6. БИФУРКАЦИОННАЯ ДИАГРАММА

Рассмотрим нелинейную динамическую модель (5.1.1) с двумя параметрами

= fi{xi.....Хп, а, Р), 1=1, 2, ...,п.

(5.6.1)

Будем исследовать поведение стационарных состояний системы (5.6.1) и их устойчивость в параметрической плоскости р- а . В частности, нас будут интересовать критические значения этих параметров, при которых возникают бифуркации - изменения числа решений илн изменения характера устойчивости отдельных решений.

В § 5.4 мы научились определять координаты точки поворота (л;, ..., Jc*, а*=ао) при выбранном значении параметра Р=Ро-Используя алгоритм продолжения, можно найти зависимость координат точки поворота от параметра р. Таким образом, в параметрической плоскости (р -а) мы получаем некоторую кривую, которую в дальнейшем мы будем называть кривой точек поворота или линией кратности. Схематически эта кривая изображена на рис. 5.15. Если мы непрерывно изменяем значения параметров а и р, то при каждом переходе через линию кратности число стационарных решений изменяется на два. Следовательно, если известны все линии кратности, то они

делят параметрическую плоскость р - а на некоторые области, в каждой из которых число стационарных решений остается постоянным. Точно так же, как и кривые точек поворота, мы можем построить кривую точек ветвления.

Аналогично мы можем находить точки комплексной бифуркации (бифуркации Хопфа) х+, а+) при изменении значений параметра р (см. рис. 5.16). Построенную таким образом кривую в параметрической плоскости р - а мы будем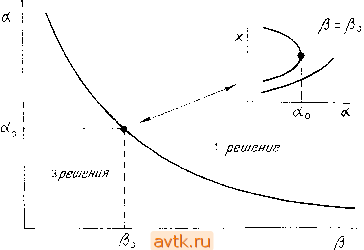

Рис. 5.15. Схематическое изображение процесса построения кривой точек поворота на бифуркационной диаграмме.

называть кривой точек комплексной бифуркации, или бифуркации Хопфа (их называют также линии нейтральности .- Ред.). Наиболее интересными представляются те точки комплексной бифуркации, в которых (при изменении одного параметра) меняется устойчивость стационарного решения. Если мы изменяем параметры р и а таким образом, что пересекаем указанную кривую точек комплексной бифуркации, то при этом изменяется устойчивость одного из имеющихся стационарных решений задачи. Мы можем построить также кривые точек комплексной бифуркации, в которых устойчивость стационарного решения не меняется - эти кривые позволяют судить о рождении неустойчивых периодических решений.

Построив в параметрической плоскости р - а кривые точек поворота и кривые точек комплексной бифуркации, мы получаем так называемую бифуркационную диаграмму. При этом

ПЛОСКОСТЬ р - а оказывается разделенной на области, в которых число стационарных решений и их устойчивость остаются неизменными. 21

Рассмотрим сначала построение бифуркационной диаграммы в простом случае, когда мы могли воспользоваться методом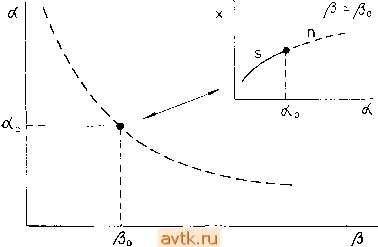

Vm. 5.16. Схематическое изображение процесса построения кривой точек комплексной бифуркации (бифуркации Андронова -Хопфа) на бифуркаци- онной диаграмме; s - устойчивое стационарное решение, п - неустойчивое.

отображения параметра. Так, для задачи 1, согласно формуле (5.2.4) из § 5.2, мы имели

Р (е - во) + ле

Da =

(. е-11в-)ехр-

(5.6.2)

Далее, в § 5.4 для нахождения точки поворота на зависимости в(Оа) из условия dDa/d& = Q мы получили квадратное уравнение относительно 0 следующего вида:

(Л, Y, В, Р, в,)в2+&(Л, Y, В, Р, в,)в + с(Л, Y, В, р, в,) = 0.

(5.6.3)

Таким образом, для нахождения точки поворота (9*, Da*) мы имеем два уравнения (5.6.2) и (5.6.3). Для построения бифуркационной диаграммы в плоскости параметров В - Da нам иужно было бы теперь продолжить решение (9, Da) уравнений t(5.6.2) и (5.6.3) в зависимости от параметра В. Однако здесь

МЫ можем воспользоваться следующим более простым способом:

a) Выберем значение ве(вс, 5).

b) Из уравнения (5.6.3) найдем значение параметра В (это уравнение линейно относительно В).

c) Из уравнения (5.6.2) подсчитаем значение параметра Da.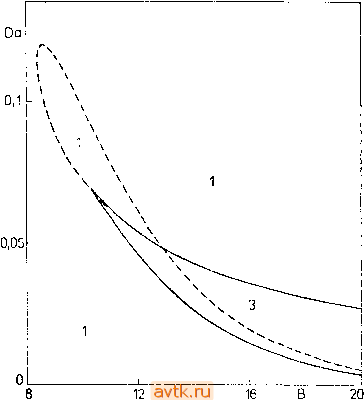

Рис. 5.17. Бифуркационная диаграмма задачи 1; у-оо, Л = 0,5, р == 0,8, вс = 0; сплошная линия - кривая точек поворота, штриховая линия - кривая точек бифуркации Андронова - Хопфа. В отдельных областях указано число стационарных решений.

Если мы получим физически разумные значения параметров В и Da (в данном случае положительные), то найденная пара чисел будет задавать точку на линии кратности (кривой точек поворота) бифуркационной диаграммы (см. рис. 5.17). На рис. 5.18 приведены несколько различных диаграмм решений.