или

Vk=l (5.4.14)

при заданном k. Уравнения (5.4.0), (5.4.12) и (5.4.13) (или (5.4.14)) образуют систему 2п--1 нелинейных уравнений относительно 2п -f- 1 неизвестных составляющих х, v, а. Решение этой системы можно искать, например, с помощью метода Ньютона. Построение матрицы Якоби для применения метода Ньютона требует вычисления вторых производных функций ft или использования соответствующих разностных формул. Заметим, что в случае п= I метод, описываемый формулами (5.4.12), (5.4.14), оказывается тождественным подходу (5.4.5), поскольку условие для функции fn+i (5.4.1) идентично соотношению (5.4.12).

Другой метод нахождения точек поворота основан на использовании условия

=0 (5.4.15)

при соответствующим образом выбранном k. Условие (5.4.15) вместе с системой (5.4.0) вновь образует систему п+ I нелинейных уравнений относительно неизвестных Xi, Х2, ..., -v , а. Левую часть формулы (5.4.15) можно найти как последнюю составляющую вектора v, т. е. решая систему линейных алгебраических уравнений

j,(x, a)-V = -,

где матрица определяется формулой (5.2.12). При п=1 условие (5.4.15) вновь оказывается эквивалентным соотношению (5.4.5).

Более просто определяются точки поворота в тех случаях, когда мы можем воспользоваться методом отображения параметра (см. п. 5.2.1). Продемонстрируем эту процедуру на примере нахождения точек поворота в задаче 1. (В этом при.мере

detJ = 0 можно записать иначе: должен существовать не равный нулю вектор V, такой, что

J(x, a)v = 0. (5.4.12)

Этот вектор определен с точностью до постоянного множителя, и поэтому к соотношению (5.4.12) добавляется еще условие нормировки вектора v, например,

ti?=l (5.4.13)

Da =

[Д-е- P<Q-Q-)J [Лв+Р(в-в,)].ехр- =

= g(e, л, Y, в, р, в,). (5.4.16)

В точке поворота имеет место условие dDa/dQ = 0, или

Если мы найдем корень в* уравнения (5.4.17) при фиксированных значениях параметров Л, у. В, и вс, то из формулы (5.4.16) получим значение Da* в точке поворота. Проведя дифференцирование в (5.4.17), после некоторых преобразований мы получаем квадратное уравнение относительно неизвестной в. Тем самым можно найти максимум два положительных корня в, которые соответствуют точкам поворота на диаграмме решений- зависимости от Da (см. также данные табл. 5.3).

5.4.2. Продолжение решения из точки ветвления

В предыдушем пункте мы рассмотрели некоторые методы нахождения точек ветвления на диаграмме решений. В § 3.4 были получены соотношения для определения касательных векторов ветвей решения, отходяших из данной точки ветвления. В то время как процедуры для определения точек ветвления носили итерационный характер, угловые коэффициенты ветвей разыскивались с помощью различных финитных подходов, основанных на методе исключения Гаусса (точка ветвления предполагалась известной заранее). В настоящем пункте мы опишем, как используются эти сведения для процесса продолжения по параметру, т. е. построения диаграммы стационарных решений (см. [5.12]).

При этом мы будем предполагать, что имеет место случай общего положения : ранг матрицы Якоби J и расширенной матрицы J понижается только на 1:

rank J = rank 3 = п- I.

Указанный алгоритм состоит из 9 шагов:

1. Нахождение точки ветвления (л:**, а**), см. п. 5.4.1.

2. Вычисление частных производных функций ft в этой точке, построение матрицы J по формуле (3.3.3).

-г. , о/гч -в

одна переменная в и один живой параметр Da. - Ред.) В п. 5.2.1 мы вывели соотношение (5.2.4), из которого находим

Иа - dxida iaa да

в этих обозначениях системы (3.4.2) и (3.4.3) переписываются в виде

ДМ. = -п. /=1, 2, -1, (3.4.2а)

tniU=-fia /=1, 2, -1. (3.4.3а) Дифференцируя соотношение (3.4.2а) по хи находим

t = -1 \ 2/; ф;, +1 {ПМ ф;.1 - fш.

г = 1, 2, и-1. (5.4.21)

Аналогичным образом, дифференцируя формулу (3.4.2а) по а, получаем

1-Z f - г-. ft -2

i=l, 2, и-1. (5.4.22)

3. Решение двух систем линейных алгебраических уравнений (3.4.2) и (3.4.3) с целью нахождения частных производных

Ж- = .....п. (5.4.18)

Это решение можно получить, применяя метод исключения Гаусса для двух различных правых частей одновременно, поскольку системы (3.4.2) и (3.4.3) имеют одну и ту же матрицу.

4. Нам потребуются частные производные второго порядка от функции F{xua), даваемой формулой (3.3.11а). С этой целью вычислим производные функции f, в точке {х**, а**):

Г-£й. f -А г -- V (54191

Значения частных производных первого порядка мы уже нашли иа шаге 2. Обозначим аналогично производные функций ф,-:

(5.4.20)

Наконец, дифференцирование (3.4.3а) по а дает

г = 1, 2, и-1. (5.4.23)

Соотношения (5.4.21), (5.4.22) и (5.4.23) представляют собой 3 системы линейных алгебраических уравнений относительно неизвестных ф^ , ф^, ф^ц, обладающие одинаковой матрицей. Тем самым, с помощью метода исключения Гаусса их можно решать одновременно. (Правые части систем составлены из величин, численные значения которых уже определены на предыдущих шагах алгоритма.)

5. Находим частные производные второго порядка для функции F, задаваемой формулой (3.3.11а):

п р п

ах, Яа п1а г/ ,

дх\ да

1 = 2 L

+ЕМа)ф;.

(5.4.24)

-да = fnaa + S 2/п/аФ/а + /п/Ф/аа + {fnjkL) Ф/а 1 = 2 L fe=2

6. Строим стартовые точки для алгоритма продолжения, например, алгоритма DERPAR (см. п. 5.2.3). Выбираем две малые числовые постоянные

h: > О, /г„ > 0. (5.4.25)

7. По крайней мере одно из двух искомых направлений ответвления характеризуется конечным значением производной dxi/da (см. (3.2.4)). Если оба значения производной оказываются конечными, то, выбирая меньшее из этих двух значений, полагаем

направление 1:

(5.4.26)

dxi

где Si вычисляется согласно формуле (3.2.6). Другое направление характеризуется конечным значением производной da/dxi и, следовательно,

направление 2:

da dx.

(5.4.27)

8. С помощью полученных таким образом двух характеристи-ческих направлений мы находим четыре исходных точки для

Таблица 5.7. Стартовые точки для процесса продолжения. Для каждого направления мы получаем две точки, одну для Р = \ и другую для Р = -1. Здесь Л^, - параметры направления для процесса продолжения, k - индекс переменной, которая остается фиксированной в ходе ньютоновских итераций для уточнения стартовой точки.

процесса продолжения решения (см. табл. 5.7). Здесь использовано то, что изменение остальных переменных подчиняется соотношениям

+ (5.4.28)

лли

(5.4.29)

в таблице приведены также направляющие параметры Л^,- для каждой из переменных (см. алгоритм в п. 5.2.3) и индекс k переменной, которая не изменяется в ходе итераций метода Ньютона для уточнения стартовой точки.

9. По окончании проведения ньютоновских итераций мы можем проконтролировать, соответствуют ли найденные стартовые

ТОЧКИ (хи Хп,а) предсказанным точкам; например, для направления 1 это можно сделать с помощью оценок

< 8, / = 2.....л.

--Ь.

(5.4.30).

<е.

Для направления 2 тестовая оценка производится аналогично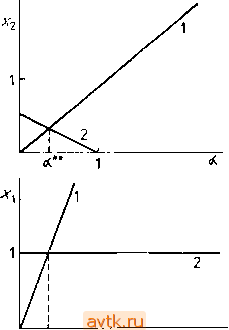

л 1 Л

Рис. 5.8. Диаграмма решений задачи (5.4.31) в окрестности точки бифуркации;.

Проиллюстрируем применение описанного алгоритма на следующем примере:

f = x - 2x - a - х^х^ - Зх + x- 2x1 - = О,

f, = xl- х1х\ + аЧ\ - = 0. (

Сходимость метода Гаусса-Ньютона (5.4.8) к точке ветвления х** = (1, 1/3), а** = 1/3 показана в табл. 5.8. Ход вычислений представлен в табл. 5.9, а поведение ветвей решения изображено* графически на рис. 5.8.

Таблица 5.8. Сходимость метода Гаусса - Ньютона к точке ветвления для системы (5.4.31).

Итерация

О

2 3 4

1,000 0,992 0,996 1,000 1,000

1.000 0,497 0,348 0.333 0,333

1,000 0,502 0,349 0,333 0,333

Исследуем теперь характер разветвления в точках первичной бифуркации для задачи о двух реакторах с модельной реакцией типа брюсселятор (см. задачу 8). В качестве параметра а выберем параметр D\, полагая D2 = Di/p, р==0, 1. Независимо от Di в задаче существует тривиальное стационарное решение Xi = Х2 = А, Yi = Y2 = В/А. Матрица Якоби для правых частей оказывается равной (если расположить переменные в порядке Xi, Yi, Х2, У2)

-(В-Ц)-Ь2Х,7,-а

В-2Х,Г,

а О

1 -О

10а

10а

О

О

10а

-{B + l) + 2X2Y2-a Xl

В - 1X2

10а

.!я, следовательно, в случае тривиального решения мы имеем

г S - 1 - а Л2 а

-В -Л^-Юа О

а О fi- 1 -а

О

10а

-В

О

10а Л2

-Л2- 10а -J

Положим Л = 2, В = 6. После соответствующих вычислений лаходнм, что значения параметра а, прн которых матрица Якоби имеет нулевое собственное число, равны 0,0443 и 2,256. Таким образом, мы имеем две точки бифуркации (2; 3; 2; 3; 0,0443) и (2; 3; 2; 3; 2,256). Направления ветвей решения в первой нз них, полученные с помощью описанного выше алгоритма, приведены в табл. 5.9. Эти результаты хорошо согласуются л диаграммой решений, представленной на рнс. 5.9; точка

Ф21 = 0,5, = 0,5.

л = -1,3333, в = 2, С = 0; 5, = йл:,/йа = О, йлгг/йа =-0,5; 52 = : da/dxi = 0,3333, dXi/dxi = 0,3333.

Стартовые точки (Ai = Ац = 0,01):

b) Направления разветвления в точке первичной бифуркации (2, 3, 2, 3,. 0,04433) для задачи 8. Л = 2, В = 6, р = 0,1.

а) Ход вычвслений для точки ветвления (1; 0,3333; 0,3333) из примера! (5.4.31).

2.6667 -5,3333 -2,6667-L О О О .

бифуркации является здесь одновременно и точкой ветвления, и сточкой поворота .

?>ис. 5.9. Диаграмма стационарных решений задачи 8, N = 2; А = 2, S = 6,

р = 0,1.

При построении диаграммы решений важной проблемой яв-.ляется отыскание всех ветвей решения. Наряду со случайным выбором начальных приближений для метода Ньютона (см. §5.1) мы можем теперь воспользоваться еще одной возможностью.

) Р = (х*, а', Ог) - точка иа двумерной поверхности S = {х, Oj, Ог е е R f (х, Oj, 02) = о}, являющаяся изолированной точкой в пересечении S с плоскостью 02 = Oj. - Ярим. ред.

С ПОМОЩЬЮ генератора случайных чисел будем формировать начальные приближения для алгоритмов нахождения точек, поворота н особенно точек ветвления. К каждой найденной точке поворота нлн точке ветвления мы применяем алгоритм продолжения по каждой ветви, отходящей от этой точки, заканчивая процесс продолжения по достижении уже известной точки ветвления или точки поворота. Основная трудность здесь состоит в том, чтобы с помощью данного алгоритма не просчитывать некоторые ветви решения дважды или четырежды.

5.4.3. Возникновение изол на диаграмме решений

Возникновение и существование изол на диаграмме решений, мы попытаемся объяснить с помощью двухпараметрической системы уравнений

ftixu Х2.....л: , щ, 02) = О, г = 1, 2.....п. (5.4.32)

Принимая во внимание сложности графического представления такой системы, будем полагать в ней =1, т. е. рассматривать уравнение вида

/i(a: аь а2) = 0. (5.4.32а)

Множество S(/i) = {(a:i, щ, Ог) е R f, (л: 02) = 0} представляет собой в общем случае некоторую поверхность в R. Пред- положим, что эта поверхность имеет вид параболоида вращения с вершиной в точке Р, ось которого параллельна оси 2 (см. рис. 5.10). Зафиксируем теперь параметр аг в формуле (5.4.32а), полагая aj = 0.2- Мы получаем уравнение с одним параметром, диаграмма решений которого представляет собой пересечение-множества S(fi) (параболоида вращения) с плоскостью а2=а2. На рнс. 5.10 видно, что при < это пересечение пусто, прн 5.2 = 0 оно вырождается в точку Р, а при cij > указанное пересечение представляет собой некоторую замкнутую кривую. Ортогонально проектируя эту замкнутую кривую на плоскость xl - ai, мы получаем в этой плоскости искомую изолу. Описанная ситуация схематически представлена на рис. 5.11.

Сформулируем теперь необходимые условия, позволяющие определить точку Р'> для системы общего вида (5.4.32). В окрестности этой точки переменную аг можно рассматривать