а) Пусть А = Bi ... Вп, где А, Bi - матрицы с положительными опреде.штелями. Если все Bj можно соединить с Е непрерывной кривой, то это верно и для А.

Действительно, пусть В jit) - такие непрерывные кривые в пространстве невырожденных матриц, что В/(0)= Bj, 6,(1) = Е. Тогда кривая А {t) = Bi(t) ... Bn(t) соединяет А с Е.

б) Если А можно соединить непрерывной кривой с В, а В с Е, то моокно соединить Л с Е..

Действительно, если A{t) такова, что /4(0)== Л, А(\)~В, и B{t) такова, что В(0) = В, fi(l) = £, то кривая

. при О <1/2,

f/1(20 IB(2-

1) при 1/2<<1

соединяет А с Е. Трюк с изменением масштаба и начала отсчета / использован лишь потому, что мы условились параметризовать кривые матриц числами /е[0, 1]. Очевидно, можно пользоваться любыми промежуточными интервалами параметризации, проводить последовательно все нужные деформации и менять масштаб лишь в конце. Поэтому дальше мы не будем заботиться об интервалах параметризации.

в) Любую квадратную невырожденную матрицу А моокно представить в виде произведения конечного числа элементарных матриц следующих типов: Fs,i, Fs,t{), ЕзЩ, ЛеК. Обозначим через Est матрицу с единицей на иесте (s, t) и нулями на остальных местах. Тогда по определению

Fs.t = E - E,s - Eft + Est -f Efs;

ps.t mE-h XEsT, f ЛJ) = £ + (> - 1)

Этот результат доказан в книге Введение в алгебру , гл. 2, § 4, следствие из теоремы п. 5.

г) Пусть теперь матрица Л представлена в виде произведения элементарных матриц. Предполагая ее определитель положительным, покажем, как соединить ее с £ с помощью нескольких последовательных деформаций, пользуясь результатами шагов а) и б).

Прежде всего, det f s, ((?) = 1 при всех X и Fs,t{0) = E. Меняя в исходных сомножителях К от начального значения до нуля, мы можем деформировать все такие множители в Е, так что можно считать, что их нет с самого начала.

Матрицы Fs{X) диагональны: на месте (s, s) стоит К, на оста.дь-ных -единицы. Изменим к от начального значения до -fl или -1 в соответствии со знаком начального значе1шя. Результатом деформации будет либо единичная матрица, либо матрица линейного отображения, меняющего один из базисных векторов на противоположный и оставляющий остальные на месте.

Результатом деформации А на этом этапе будет матрица композиции двух преобразований: одно сводится к перестановке векторов базиса (Fs.i меняет местами s-й и .-й вектор), другое меняет знаки части векторов (композиция £5(--1) и Ft(-1)).

Любую перестановку можно разложить в произведение попарных перестановок. Матрицу перестановки векторов базиса в пло-

/0 1\ /-1 04 г-cost smt\

скости ( J qJ можно соединить с I jj кривой I 1 cost)

я/2 tO. Очевидно, разнеся элементы последней матрицы по местам (s, s), {s,t), it,s), (tj), получим соответствующую деформацию в любой размерности, уничтожающую множители fj,

К этому моменту А превратилась в диагональную матрицу с элементами ±1 на диагонали, причем число минус единиц четно,

ибо определитель А положителен. Матрицу (j~ q ) можно сое-

(1 ОЛ /cos t - sin t\ , n /; 1

P jj кривой yf cost) 0. Собрав все-I попарно и проведя такие деформации всех пар, мы завершим доказательство.

Вернемся теперь к ориентации.

Будем говорить, что базисы {е,.}, {е[} одинаково ориентированы, если определитель матрицы перехода от одного из них к другому положителен. Ясно, что множество упорядоченных базисов L разбивается в точности на два класса, состоящих из одинаково ориентированных базисов, тогда как базисы из разных классов ориентированы по-разному (или противоположно).

Выбор одного из этих классов называется ориентацией пространства L.

Ориентация одномерного пространства соответствует указанию положительного направления в нем или полупрямой R+e = а > 0}, где е - любой вектор, определяющий ориентацию.

В двумерном пространстве задание ориентации с помощью базиса {ei, 62} можно представлять себе как указание положительного направления вращения плоскости от ei к 62. Это интуитивно согласуется с тем, что базис {е2, ei) задает противоположную

ориентацию (определитель матрицы перехода равен -1) и

противоположное направление вращения.

В общем случае переход от базиса {ei} к базису [ei], состоящему из тех же векторов, но в другом порядке, сохраняет ориентацию, если перестановка четная, н меняет ее, если перестановка нечетная. Замена знака у одного из векторов в/ меняет ориентацию на противоположную.

В трехмерном физическом пространстве выбор конкретной ориентации может быть связан с физиологическими особенностями человека - асимметрией правой и левой стороны. Левая сторона - siTo та, где у подавляющего большинства людей находится сердце. Большой, указательный и средний пальцы левой руки, согнутые по направлению к ладони, в линейно независимом положении образуют упорядоченный базис, фиксирующий ориентацию ( правило левой руки ). Вопрос о том, существуют ли чисто физические процессы, позволяющие выбрать ориентацию пространства, т. е.

неинвариантные относительно зеркального отражения , был решен около двадцати лет назад положительно, ко всеобщему изумлению, экспериментом, установившим несохранение четности в слабых взаимодействиях.

УПРАЖНЕНИЯ

1. Пусть {Ц, L2, Lz)-упорядоченная тройка п.чоскостей в Х^, попарно различных. Доказать, что имеются два возможных типа взаимного расположения таких троек, характеризующихся тем, что dim Li П i-s П i-з = О или 1. Какой из этих типов следует считать общим?

2. Доказать, что тройки попарно разных прямых в все одинаково расположены, а для четверок это уже неверно.

3. Пусть LiCzLcz ... cz L - флаг в конечномерном пространстве L, т, = dimL;. Доказать, что если с:... ciL -другой флаг, m = dimL;, то автоморфизм L, переводящий первый флаг во второй, сушествует тогда и только тогда, когда = т^. для любого i.

4. То же для прямых разложений.

5. Доказать утверждения пятого абзаца п. 6.

6. Пусть р: L - проектор. Доказать, что L = Кег р Ф (т р. Вывести отсюда, что в подходящем базисе L любой проектор р представлен матрицей вида

V о 0 /

где г = dim Imp.

7. Пусть L - п-мериое пространство над конечным полем нз q элементов

а) Вычислить количество ft-мериых подпространств в L, 1 п.

б) Вычислить количесгво пар подпространств Lu L2C1L с данными размерностями Lb L2 и Ll П Lj. Убедиться, что при q оо доля этих пар, находящихся в общем положении, среди всех пар с данными dim Li, dimL. стремится к 1.

§ 6. Факторпространства

1. Пусть L - линейное пространство, Mcz L - его линейное подпространство, а / eL - вектор. Различные вопросы приводят к рассмотрению множеств вида

Z + M = {f-f т(теМ},

сдвигов линейного пространства М на вектор /. Вскоре мы убедимся, что такие сдвиги не обязаны быть линейными подпространствами в L; их называют линейными подмногообразиями. Начнем с доказательства следующей леммы.

2. Лемма, /i -Ь Mi = /г -- Ма тогда и только тогда, когда Мх = N[2 = М и ll - /2 е М. Таким образом, всякое линейное подмногообразие однозначно определяет линейное подпространство М, сдвигом которого оно является. Вектор же сдвига определяется лишь с точностью до элемента из этого подпространства.

Доказательство. Прежде всего, пусть U - /геМ. Положим 1\ - /г == гпо. Имеем

/, + М == (Zi -Ь /п| mе М}, Z2 -ЬМ = {Zi -f m - то (т е М}.

Но когда т пробегает все векторы из М, т - то тоже пробегает все векторы из М. Поэтому h -\- М = U -\- М.

Наоборот, пусть Zi + Mi = /2 + М2. Положим mo = l\ - /2. Из определения ясно, что тогда /По-f М i = Мг. Так как 0еМ2, мы должны иметь ШоеМ]. Значит, mo + Mi=Ali по рассуждению в предыдущем абзаце, так что Mi -Л12 = Л1. Это завершает доказательство.

3. Определение. Факторпространством L/M линейного пространства L по М называется множество всех линейных подмногообразий в L, являющихся сдвигами подпространства М, со следующими операциями:

а) (/. + M)-f (/2-f M)==(/,-f Z2)+M,

б) a{li -f М) = a/i -f М для любых li, /2 e L, я e Ж

Эти операции определены корректно и превращают L/M в линейное пространство над полем Ж.

4. Проверка корректности определения. Она состоит из следующих шагов:

&) Если и + М = иЛ-М и /2 + M = /2-fM. то Z,-fL-fM =

В самом деле, нз леммы п. 2 следует, что/i - U - т\ еЛ1 и L- - 4= m2S М. Поэтому снова по лемме п. 2

{и -f /2) -f М = {(, -f /2) -f (m, -f mi) + M = (/1 -f I2) + M,

ибо mi -f m2 e M.

6) Если Л -f M= A + M, mo ak -f M = a/i -f M, В самом деле, снова полагая/i - /i = meM, имеем ah - g/i= = атеМ, неприменение леммы п. 2 дает требуемое.

Таким образом, сложение и умножение на скаляр действительно однозначно определены в L/M. Остается проверить аксиомы линейного пространства. Но они сразу же следуют из соответствующих формул в L. Например, одна из формул дистрибутивности проверяется так:

о[(1 + М) + (/2 4- M)]-a((/,-f y + M) = a(Z,-f/2) + М =

= а/, -f ak + М = (а/, -f М)-f {al + М) = а(/, -f М)-a{k-\-M).

Здесь последовательно используются: определение сложения в L/M, определение умножения на скаляр в L/M, дистрибутивность в L и снова определение сложения и умножения на скаляр в L/M.

5. Замечания, а) Из определения видно, что аддитивная группа L/M совпадает с факторгруппой аддитивной группы L по аддитивной группе М. В частности, подмногообразие Mat является нулем в L/M.

б) Имеется каноническое отображение f: L-*-L/M: /(/)=/+ М. Оно сюръективно, а его слои - прообразы элементов - суть как раз подмногообразия, отвечающие этим элементам. Действительно, по лемме п. 2

f - (0 + М) = е LI /-1-Л1 =/р-Ь Л1) U е L1 / -/о е УИ) =+ М. 4У

Заметим, что в этой цепочке равенств /о+М первый раз рассматривается как элемент множества L/M, а остальные--как подмножества в L.

Из п. 4 ясно, что / - линейное отображение, а лемма п. 2 показывает, что Кег f=M, ибо 1о-\- М == М тогда и только тогда, когда lo е М.

6. Следствие. Если L конечномерно, то dim L/M = dim L - - dimM.

Доказательство. Применить теорему п. 12, § 3 к построенному отображению L->-L/M.

Многие важные задачи в математике приводят к ситуации, когда пространства М с= L бесконечномерны, а факторпростран-ство L/M конечномерно. В этом случае пользоваться следствием п. 6 нельзя, и вычисление dim L/M обычно становится нетривиальной задачей. Число dim L/M вообще называется коразмерностью подпространства М в L и обозначается codimM или codimM.

7. Поставим следующую задачу: даны два отображения /: L-> /И п g:L-N; когда существует такое отображение Л: MN, что g = hf? На языке диаграмм: когда можно вложить диаграмму

А

М 2Г

В коммутативный треугольник

(ср. § 13 о коммутативных диаграммах). Ответ для линейных отображений дается следующим результатом.

8. Предложение. Для существования h необходимо и достаточно, чтобы Кег / с: Кег g; если это условие выполнено и Im / = М, то h единствен.

Доказательство. Если h существует, из g= hf следует, что g{l) = hf{l) = 0, коль скоро Д/) = 0. Поэтому Кет fez Кет g.

Наоборот, пусть Кег / сг Кег g. Построим сначала h на подпространстве Im/c=M. Единственная возможность состоит в том, чтобы положить h{m) = g{l), если т = f{l). Нужно проверить, что h определено однозначно и линейно на 1т f. Первое следует из того, что если гп = f{li) = fik), то /j -/г е Кег / сг Кег g, откуда g{li) = g[l2). Второе следует автоматически из линейности fug.

Теперь достаточно продолжить отображение h с подпространства Im/c=M на все пространство М, например, выбрав базис Im /, дополнив его до базиса М и положив h равным нулю на дополняющих векторах.

9. Пусть g: L-*-M - линейное отображение. Мы уже определили ядро и образ g; дополним это определение, положив

кообраз g: Coim g = L/Ker g, коядро g: Coker g = Mflmg.

Имеется цепочка линейных отображений, разбирающая g на части ,

Y r-£ Coimr- Img- -Ж CoKerg-.

где все отображения, кроме Л, - канонические вложения и факторизация, а h - единственное отображение, делающее коммутативной диаграмму

Coimg--Img

Оно определено однозначно, потому что Кег с = Кег g, и является изоморфизмом, потому что обратное отображение тоже существует и определено однозначно.

Смысл объединения этих пространств в пары (с приставкой ко и без нее) объясняется в теории двойственности (см. следующий параграф и упражнение 1 к нему).

10. Конечномерная альтернатива Фредгольма. Пусть g: ->-М - линейное отображение. Число

ind g = dim Coker g - dim Ker g

называется индексом оператора g. Из предыдущего пункта следует, что если L и М конечномерны, то индекс g зависит только от L и М:

ind g = (dim M - dimlmg)-- (dim L - dim Im g) = dim M - dim L.

В частности, если dim М = dim L, например, если g -линейный оператор на L, то indg = 0 для любого g. Отсюда вытекает так называемая альтернатива Фредгольма:

либо уравнение g{x) = у разрешимо для всех у, и тогда уравнение g(x) = О имеет лишь нулевые решения;

либо это уравнение разрешимо не для всех у, и тогда однородное уравнение (л;) = О имеет ненулевые решения.

Точнее, если ind g = 0, то размерность пространства решений однородного уравнения равна коразмерности пространства правых частей, при которых разрешимо неоднородное уравнение.

УПРАЖНЕНИЯ

1. Пусть М, N с L. Доказать, что следующее отображение является линейным изоморфизмом:

(М + N)/N ->M/M(]N: т +п +N t- т +M[\N.

2. Пусть L = М Ф N. Тогда каноническое отображение

M-L/N: nn->m + N

является изоморфизмом.

§ 7. Двойственность

1. В § 1 мы поставили в соответствие каждому линейному пространству L двойственное к нему пространство L* = 2{Ь,Ж), а в § 3 показали, что если dimL < оо, то dimL* = dimL, и построили канонический изоморфизм sl: LL*. Здесь мы продолжим описание двойственности, включив в рассмотрение линейные отображения, подпространства и факторпространства.

Теория двойственности получила свое название благодаря тому, что она выявляет ряд свойств двусторонней симметрии линейных пространств, довольно трудных для наглядного воображения, но совершенно фундаментальных. Достаточно сказать, что дуализм волна - частица в квантовой механике адекватно выражается именно на языке линейной двойственности бесконечномерных линейных пространств (точнее, соединения линейной и групповой двойственности в технике анализа Фурье).

Удобно следить за этой симметрией, несколько изменив обозначения, принятые в § 1 и 3.

2. Симметрия между L и L*. Пусть /eL, fL*. Вместо f{l) мы будем писать (/, /) (в знак аналогии со скалярным произведением- но векторов из разных пространств!). Таким образом, мы определили отображение L*XL->X. Оно линейно по каждому из двух аргументов Д / при фиксированном втором:

(fi + h, = /) + {/2. 0. ( /.. /) = а(/ /). if, lx + h) = if. h) + if, k), if. alx) = a if, Z,).

Вообще, отображения Ly, М-Ж с таким свойством называются билинейными, а также спариваниями между пространствами L и М. Введенное выше спаривание между L и L* называется каноническим (ср. обсуждение этого слова в § 3, п. 8).

Отображение е^: L-L** из § 3, п. 10, как видно из его определения, можно задать условием:

(еПО. /)==(/, 0.

где слева стоит символ спаривания между L** и L*, а справа - между L* и L. Если dimL < оо, так что et является изоморфизмом, и мы условимся отождествлять L** и L посредством ei, эта формула приобретает симметричный вид (l,f) = (f,l). Иными словами, мы можем также рассматривать L как пространство, двойственное к L*.

S. Симметрия между двойственными базисами. Пусть (ei, ... с„} - базис в L, {е\ .... е } - двойственный базис в L*. Согласно п. 9 § 3 он определяется формулами

О при / ф k.

{е', eft) = 6,ft =

. 1 при i - k.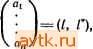

Симметрия (е', ek) = {ek, е') в соглашениях предыдущего пункта означает, что базис (е*) двойствен к базису (е'), если L рассматривать как пространство линейных функционалов на L*. Таким образом, (е') и (е^) образуют двойственную пару базисов, и это отношение симметрично.

п

Представим вектор 1* L* в виде линейной комбинации Z 6,е',

п

а вектор 1 L в виде Z уСу. Тогда

: =

ЬпУ

{Р)ь = Ф)а^{Ь„ .... 6 )

->

где а, b - вектор-столбцы соответствующих коэффициентов. Эта формула совершенно аналогична формуле для скалярного произведения векторов в евклидовом пространстве, однако связывает в этой ситуации векторы из разных пространств.

4. Двойственное, или сопряженное отображение. Пусть f: L -> ->М - линейное отображение линейных пространств. Мы покажем сейчас, что существует единственное линейное отображение /*: M*->-L*, которое удовлетворяет условию

(Г(т-), 1) = {т; fit))

для любых векторов т* е М*. L.

а) Единственность /*. Пусть / *, Ц - та таких отображения. Тогда (f; (m*), /) = {/n*, f {/)) = (f; (m), I) для всех weM*, / ge L, откуда следует, что((/, - fj) (m*),/) = 0. Фиксируем m* и будем менять/. Тогда элемент (/-/*) (m) sL как линейный функционал на L принимает только нулевые значения и, значит, равен нулю. Поэтому f = f2-

б) Существование f*. Фиксируем т* е М и рассмотрим выражение (m*,f{l)) как функцию на L. В силу линейности / и билинейности (,) эта функция линейна. Значит, она принадлежит L*. Обозначим ее через /*(т*). Равенства

Г {т\ + ml) = / (m;) + Г К), Г {am*) = af )

следуют из линейности (/??*, f(l)) по т*. Значит. /*-линейное отображение.

Пусть в L, М выбраны некоторые базисы, а в L*, М* - двойственные базисы. Пусть f в этих базисах представлено матрицей Л Мы утверждаем, что /* в двойственных базисах представлено транспонированной матрицей А'. В самом деле, пусть В - матрица /*. Согласно определениям и п. 3 имеем, обозначив вектор-столбцы

координат т*, I через а, Ь,

(т, !(1)) = а*{м},

{Г{т*), 1) = {ваУь = СаВ'Уь.

Из ассоциативности умножения матриц и единственности /* следует, что А = В', т. е. В = А'.

Основные свойства сопряженных отображений собраны в следующей теореме:

5. Теорема, а) {f + g)* = f* + g*;

б) (al)*=af*\3decblg\

в) {ЫГ = ёТ; здесь L-M-N;

г) id* = id, О* = 0;

д) если канонически отождествить L** с L и М** с М, то f**: L** М** отождествляется с f: L-M.

Доказательство. Если считать, что L и М конечномерны, то проще всего проверить все эти утверждения, представив f, g матрицами в двойственных базисах и воспользовавшись простыми свойствами операции транспонирования:

{аА + ЬВУ = аЛ + ЬВ\ (ЛВ) = ВМ, Е* = Е, 0 = 0, (Л') = 0.

Инвариантную проверку мы оставляем читателю в качестве упражнения.

6. Двойственность между подпространствами в L и в L*. Пусть MczL - некоторое линейное подпространство. Обозначим через

сг L* и будем называть ортогональным дополнением к М множество функционалов, обращающихся в нуль иа М. Иными словами,

т' е M <=i- (т*, т) = 0 для всех т е М.

Легко видеть, что M является линейным пространством. В следующих утверждениях собраны основные свойства этой конструкции (L предполагается конечномерным).

а) Имеется канонический изоморфизм L*/M- -М*. Строится он так: многообразию Г -f М^ ставится в соответствие ограничение функционала /* на М. От выбора /* оно не зависит, ибо ограничения функционалов из M-- на М нулевые. Линейность этого отображения очевидна. Оно сюръективно, ибо всякий линейный функционал на М продолжается до некоторого функционала на L.

В самом деле, пусть {ci, ..., em} - базис в М, (ei, ..., Ст, em+i.....е }-его продолжение до базиса L. Функционал / на М,

заданный значениями f(ei), f{en), продолжается на L, например, если положить /{£, 41) = ... = /(е^) = 0.

Наконец, построенное отображение L*/M М* инъективно. В самом деле, у него нулевое ядро: если ограничение I* на М равно нулю, то 1*М^ и /* += M-i-- нулевой элемент из L*/M-.

б) dim М -f- dim М- - == dim L. Действительно, это следует из предыдущего утверждения, следствия п. 6 § 6 и того, что dim L* = = dim L, dim М* = dim М.

в) При каноническом отождествлении L** с L пространство {M-) совпадает с М.

Действительно, так как (т*, т) - О для всех гп* и данного т^М, ясно, что М с:{М^). Но, кроме того, по предыдущему свойству, примененному дважды,

dim (A/J-)- = dim L - dim AfJ- = dim M.

Значит, Af =(MJ-) 4

r) (M, -f M) = Alf n AfJ-; (AI, П My = M{- + Mj-.

Доказательство предоставляется читателю в качестве упражнений.

УПРАЖНЕНИЯ

1. Пусть с линейным отображением g: L->-M конечномерных пространств связана цепочка отображений, построенных в п. 8 § 6. Построить канонические изоморфизмы

Кег g* -> Coker g, Coim g* -> Im g, Im > Coim g, Coker g* -> Ker g.

2. Вывести отсюда третью теорему Фредгольма : для того чтобы уравнение g{x)- у было разрешимо (по х при данном у), необходимо и достаточно, чтобы у был ортогонален к ядру сопряженного отображения g*: M*~L*.

f я

3. Последовательность линейных пространств и отображений L -> М -> называется точной в члене М, если Im / = Кег g. Проверить следующие утверждения:

а) Последовательность О-> L -> М точна в члене L тогда и только тогда, когда f - инъекция.

б) Последовательность М -> N --> О точна в члене тогда и только тогда, когда g - сюръекция.

f fi

в) Последовательность конечномерных пространств О -> L -> М ->>

->- N -* О точна (во всех членах) тогда и только тогда, когда точна двой -

fi* f*

ствённая последовательность О -> Л^* -> М* ->- L* -> 0.

4. Мы знаем, что если отображение р. L->- М в некоторых базисах представлено матрицей А, то отображение f* в двойственных базисах представлено матрицей А'. Вывести отсюда, что ранг матрицы совпадает с рангом транспонированной матрицы, т.е. что максимальные числа линейно независимых строк и столбцов матрицы совпадают.

§ 8. Структура линейного отображения

1. В этом параграфе мы начнем изучать следующую задачу: возможно яснее геометрически представить себе устройство линейного отображения f: L->M. Ответ совсем прост, когда L а М никак