можем найти единственное проективное отображение, переводящее в р\ для всех 1 г /г 4- 2, но рп+з попадает или не попадает в р^з в зависимости от ситуации.

Нетрудно описать проективные инварианты системы из л + 3 точек. Выберем систему однородных координат в Р, в которой первые п-\-2 точки имеют координаты, описанные в случае б). В ней точка ph+3 имеет координаты (х\: x +i), определенные однозначно с точностью до пропорциональности. Любой проективный автоморфизм Р, примененный одновременно к конфигурации {ри рп+з} И К приспособленной к ней системе координат, переведет эту конфигурацию в другую, а систему координат - в приспособленную систему координат новой конфигурации. Поэтому координаты (xf. ...: x +i) последней точки останутся теми же самыми.

Все предыдущие рассуждения с очевидными видоизменениями переносятся также на случай, когда у нас имеются два -мерных проективных пространства Р и Р', конфигурации {ри р^} cz Р и {р[, ..., р^} CZ Р', и мы интересуемся проективными изоморфизмами Р->Р', переводящими первую конфигурацию во вторую. Резюмируем результаты обсуждения в следующей теореме:

8. Теорема, а) Пусть Р, Р' - п-мерные проективные пространства, {p, р„+2} сгР и {р[, р^ 2} czP - две системы точек в общем положении. Тогда существует единственный проективный изоморфизм Р -)- Р', переводящий первую конфигурацию во вторую.

б) Аналогичный результат верен для систем n-f-3 точек в общем положении тогда и только тогда, когда координаты {п -f 3) -Й точки в системе, приспособленной к первым о -f 2 точкам, для обеих конфигураций совпадают (конечно, с точностью до скалярного множителя).

9. Двойное отношение. Применим теорему п. 8 к случаю о = 1. Мы получим, прежде всего, что если на двух проективных прямых заданы упорядоченные тройки попарно разных точек (это и есть здесь условие общности положения), то существует единственный проективный изоморфизм прямых, переводящий одну тройку в другую.

Далее, пусть задана четверка попарно разных точек {pi, рг, рз, pj сг Р' с координатами (1:0), (0:1), (1:1) и {xy-.xi) в приспособленной системе. Тогда хг ф 0. Положим

[Р2. Рз. Рр Pj = X,X2 -

Это число называется двойным отношением четверки точек {р,}. Необычный порядок объясняется желанием сохранить согласованность с классическим определением: в аффинной карте, где рг = схэ, рз==0, pi = l, координаты точек в квадратных скобках располагаются так: [О, 1, оо, х], где х и есть двойное отношение этой четверки.

Сам термин двойное отношение происходит из следующей явной формулы для вычисления инварианта [хь Х2, хз, Xi], где хгеЖ

на сей раз понимаются как координаты точек р,- в произвольной аффинной карте Р'. Согласно результатам п. 4 группа PGL(l) в этой карте представлена дробно-линейными преобразованиями

вида х1- , ad - 6с 0. Такое преобразование, переводя-

щее {хи Х2, хз) в (О, 1, оо), имеет вид

XI-X . Xi - Xi

Хз - X Л^з - Х2

Подставляя сюда х = xt, находим

г Xi - Х4 Xi - Х2

lx Хз, Xi] - : з ,

Еще одна классическая конструкция, связанная с утверждением а) теоремы п. 8 для п= \, описывает представление симметрической группы S3 дробно-линейными преобразованиями. Согласно этой теореме любая перестановка {рь рг, Рз)- {Ро(1), Ро(2), Ро(3)} трех точек на проективной прямой индуцирована единственным проективным преобразованием этой прямой.

В аффинной карте, где {pi, рг, рз} = {О, 1, оо}, эти проективные преобразования представлены дробно-лннейными преобразованиями

f 1 , 1 х-\ X \

х^{х,, 1-х,-. -, -}.

Перейдем теперь к изучению проекций.

10. Пусть линейное пространство L представлено в виде прямой суммы двух своих подпространств размерности 1: L = Li Ф Lg. Положим P = P{L), PiP{Li).

Как было показано в п. 1, линейная проекция L->L2, tih + /2) = /2, е Li, индуцирует отображение

Р{Л:Р\Р,->Р2,

которое мы будем называть проекцией из центра Р\ на Р2. Чтобы описать всю ситуацию в чисто проективных терминах, заметим следующее.

а) dimP,-f dimP2= dimP-1 и P, ПР2=0. Наоборот, любая конфигурация (Р\, Рг) с такими свойствами происходит из единственного прямого разложения L = Li Ф L2.

б) Если аеРг, то P{f)a = a; если ceP\{PiUP2), то P{f)a определяется как точка пересечения с Рг единственной проективной прямой в Р, пересекающейся с Pi и Рг и проходящей через а.

Действительно, случай а^Рч очевиден. Если Р| U Рг, то на языке пространства L нужный нам результат формулируется так: через любую прямую Lo cz L, не лежащую в Li и L2, проходит единственная плоскость, пересекающаяся с Li и Lg по прямым, и ее пересечение с Lg совпадает с ее проекцией на Lg. В самом деле, одна плоскость с этим свойством есть: она натянута на проекции Lo на L и Lg соответственно. Существование двух таких плоскостей

влекло бы существование двух разных разложений ненулевого вектора keLo в сумму двух векторов из I, и L2 соответственно, что невозможно, ибо L = L\® Li-

Поскольку описанная проективная конструкция отображения Р->Р\Р\ поднимается до линейной, мы сразу же получаем, что для любого подпространства Р' сг Р\Р\ ограничение проекции P->Pi является проективным отображением, т. е. имеет вид P{g), где g - некоторое линейное отображение соответствующих векторных пространств.

В важном частном случае, когда Pi -точка, Рг -гиперплоскость, отображение проекции из центра Р) на Рг переводит точку а в ее образ на Рг, видимый наблюдателем из Pi. Поэтому отношение между некоторой фигурой и ее проекцией в таком случае называют еще перспективным. Интуитивно менее очевидна, например, проекция из прямой на прямую в Р^ (рис. 5, 6).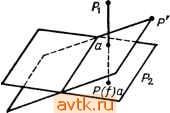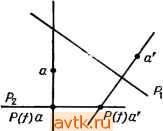

Рис. б

Рис. 6

Важное свойство проекций, которое следует иметь в виду, состоит в следующем: если Р' сг Р\Р\, то проекция из центра Р| определяет проективный изоморфизм Р' и его образа в Рг- Действительно, на языке линейных пространств это означает, что проекция /: Ll Ф £г- Li индуцирует изоморфизм М с /(М), где Ма L - любое подпространство с LiflM- {0}. Это так, ибо L, ==Кег/.

11. Поведение проекции вблизи центра. Ограничимся дальше рассмотрением проекций из точки pi = а е Р и попытаемся понять, что происходит с точками, находящимися вблизи центра. В случае X - R и С, когда действительно можно говорить о близости точек, картина такова: в точке а нарушается непрерывность проекции, ибо точки Ь, как угодно близкие к а, но подходящие к а с разных сторон , проектируются в далеко отстоящие друг от друга точки Pi. Именно это свойство проекции лежит в основе ее приложений к разного типа вопросам о разрешении особенностей . Если в Р лежит некая фигура (алгебраическое многообразие, векторное поле), имеющая вблизи точки а необычное строение, то, проектируя ее из точки а, мы можем растянуть окрестность этой точки и увидеть, что в Heff прои-холчт. в увеличенном масштабе, причем коэффициент увеличения при приближении к а безгранично растет.

Хотя эти приложения относятся к существенно нелинейным ситуациям (тривиализируясь в линейных моделях), стоит разобраться в структуре проекции вблизи ее центра несколько подробнее, насколько это можно сделать, оставаясь в рамках линейной геометрии.

12. Введем в P{L) проективную систему координат, в которой центром проекции является точка (О, О, 1), а Р2 = Р - состоит из точек (хо: xi: Xn-i: 0); чтобы добиться этого, следует выбрать в L базис, являющийся объединением базисов в Ц и Ц (поскольку центр - точка, dim Li = 1).

Нетрудно видеть, что тогда точка (хо: ...: Хп) проектируется в (хо: Хп-ь 0). Дополнение Л к Рг снабжено аффинной системой координат

(уо, Уп-)-=(хо/х„, .... х„ ,/х„)

с началом О в центре проекции. Рассмотрим прямое произведение Л X Рг = Л X Р и в нем график Го отображения проекции, которое, напомним, определено только на Л\{0}. Этот график состоит из пар точек с координатами

((хо/х„, х„ /х„), (Xq : ... :х„ )),

где не все Хо, ..., x i равны нулю одновременно. Увеличим график Го, добавив к нему над точкой ОеЛ множество (0}ХР -с^ХР -.

Г = Гои(0}ХР -,

в соответствии с геометрической интуицией, согласно которой при проекции из О центр переходит во все пространство Р -1 .

Pjj Множество Г обладает рядом хоро-

ших свойств.

а) Г состоит в точности из пар точек

удовлетворяющих системе алгебраических уравнений yiX] - y/Xi = 0; г, У == О.....п - 1.

Действительно, эти уравнения означают, что все миноры матрицы

(Хо . Хп-\ л рдз,ц нулю, так что ее ранг равен единице (ибо пер-Уй Уп-\ }

вая строчка ненулевая) и, значит, вторая строка пропорциональна первой. Если коэффициент пропорциональности не равен нулю, мы получаем точку из Го, а если равен, то из {0} X Р -

б) Отображение ГЛ: ((уо, .., Уп-л), (хо:...: х„ ,))->((/о, уп-\) является биекцией всюду, кроме слоя над точкой {0).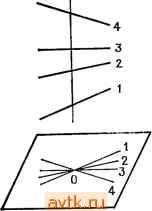

Иными словами, Г получается из А вклеиванием целого проективного пространства Р - вместо одной точки. Говорят, что Г получается из А раздутием (blowing up) точки, или о-процессом с центром в точке О. Прообраз в Г каждой прямой в А, проходящей через точку О, пересекает вклеенное проективное пространство рп-1 также по одной точке, но своей для каждой прямой. В случае Х = R, п == 2 можно представлять себе аффинную карту вклеенного проективного пространства Р\ как ось винта мясорубки Г, делающего полоборота на протяжении своей бесконечной длины (рис. 7).

Реальное применение проекции к исследованию особенности в точке О е. А связано с переносом интересующей нас фигуры с А на Г и рассмотрению геометрии ее прообраза вблизи вклеенного пространства Р -. При этом, например, прообраз алгебраического многообразия будет алгебраичен благодаря тому, что Г задается алгебраическими уравнениями.

§ 9. Конфигурации Дезарга и Паппа и классическая проективная геометрия

1. Классическая синтетическая проективная геометрия была в значительной мере посвящена изучению семейства подпространств в проективном пространстве с отношением инцидентности; свойства этого отношения можно положить в основу аксиоматики, и прийти затем к современному определению пространств P(L) и поля скаляров Ж так, что L VI Ж появятся как производные структуры. В таком построении большую роль играют две конфигурации - Дезарга и Паппа. Мы введем и изучим их в рамках наших определений и затем вкратце опишем их роль в синтетической теории.

2. Конфигурация Дезарга. Пусть 5 -семейство точек в проективном пространстве. Символом S мы будем обозначать его проективную оболочку. Рассмотрим в трехмерном проективном пространстве упорядоченную шестерку точек (pi, рг, Рз; д\, q% дз). Предпо-лагается, что точки попарно разные и что pip2P3 и 919293 суть плоскости. Далее, пусть прямые piqi, piqi и рзз пересекаются в одной точке г, отличной от р,- и 9,. Иными словами, треугольники Р1Р2Р3 и 919293 перспективны , и каждый из них есть проекция другого из центра г, если они лежат в разных плоскостях. Тогда для любой пары различных индексов {i, j} cz {I, 2, 3} прямые р,р/ и 9,97 не совпадают, иначе мы имели бы р, =! qi, ибо р,- и 9, суть точки пересечения этих прямых с прямой piqi. Кроме того, прямые pipi и 9,9/ лежат в общей плоскости гргр/. Поэтому они пересекаются в точке, которую мы обозначим Sk, где {i, /, k} = = {1, 2, 3}: это точка пересечения продолжений пары соответствующих сторон треугольников Р1Р2Р3 и 919293-

Теорема Дезарга, которую мы докажем в следующем пункте, утверждает, что три точки si, 2, S3 лежат на одной прямой. Конфигурация, состоящая из десяти точек pi, qj, s*, г и десяти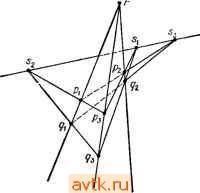

соединяющих их прямых, показанных на рис. 8, называется конфигурацией Дезарга. Каждая ее прямая содержит ровно три ее точки, и через каждую ее точку проходят ровно три ее прямые. Читателю предлагается самостоятельно убедиться в том, что она по существу симметрична (в том смысле, что группа перестановок ее точек и

прямых, сохраняющая отношения инцидентности, транзитивна как на точках, так и на прямых).

3. Теорема Дезарга. В описанных выше условиях точки s\, $2, S3 лежат на одной прямой.

Доказательство. Мы разберем два случая в зависимости от того, совпадают плоскости

Р1Р2Р3 и 9123 или нет.

а) Р1Р2Р3 919293 ( пространственная теорема Дезарга .

В этом случае плоскости pipzPs и 919293 пересекаются по прямой. Рис. 8 и нетрудно убедиться, что Si, S2,

S3 лежат на ней. Действительно, точка si, например, лежит на прямых ргрз и 9293, которые в свою очередь лежат в плоскостях Р1Р2Р3 и 919293 и, значит, в их пересечении.

б) Р1Р2Р3 = 919293 ( плоская теорема-Дезарга ). В этом случае выберем в пространстве точку г', не лежащую в плоскости рфгРз. и соединим ее прямыми с точками г, pi, pj. В плоскости rpi, лежит прямая pi9i и, значит, точла г. Проведем в ней через г прямую, не проходящую через точки г' и рь и обозначим ее пересечения с прямыми г'р rq, через р[д[ соответственно. Тройки (р^, Рз Рз) и (q[, 92, 9з) лежат уже в разных плоскостях - иначе содержащая их общая плоскость содержала бы прямые ргрз и q и потому совпадала бы с pipzPs, но это невозможно, ибо р[, q\ в этой начальной плоскости не лежат. Кроме того, прямые p\q\, pq и Рз9з проходят через точку г. В силу пространственной теоремы Дезарга точки р\р2 П 992 Р1Р3 П 99з и Р2Р3 П 929з лежат на одной прямой. Ио если спроектировать эти точки из г' на плоскость рхрчРъ, то получатся как раз &з, S2, s\ соответственно, потому что г' проектирует {р\, pg, Рз) в (р Р2, Рз) и {q\, 92, 9з) в (9 q, 93) и, значит, стороны каждого из этих треугольников в соответствующие стороны исходных треугольников. Это завершает доказательство.

4. Конфигурация Паппа. Рассмотрим в проективной плоскости две разные прямые и две тройки лежащих на них попарно разных точек pi, Р2, Рз и 9i, 92, 93. Для любой пары различных индексов

{i, /}<={!, 2, 3} построим точку Sk = piqinqiPj, где {i, /, k} = =={1.2. 3}.

5. Теорема Паппа. Точки Si, S2, ss лежат на одной прямой.

Доказательство. Проведем прямую через точки S3, S2 и обозначим через ее пересечение с прямой pii. Наша цель состоит в доказательстве того, что si лежит на ней.

Построим два проективных отображения fu fz: piPiPs-QiQigs-

Первое из них, fu будет композицией проекции pipipz на SiSz из точки 91 с проекцией S3S2 на 919293 из точки ри Очевидно, /1 (Р ) = <7t для всех t= 1, 2, 3, и, кроме того, fi(fi) = <2, где ti = = Р1Р2РзП 919293, 4 = S4S3S2 П 919293 (рис. 9).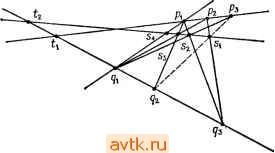

Рис. 9

Второе из них, /2, будет композицией проекции piPips на S3S2 из точки 92 с проекцией S3S2 на 919293 из точки рг. Эта композиция переводит р, в 91, р2 в 92 и в ti.

Поскольку fl и /2 одинаково действуют на тройках точек {tu Pi, Р2), они должны совпадать. В частности, /1(рз) = /2(рз). Но fi(P3) = 93- Значит, /2(рз) = 9з- Это утверждение геометрически оз-начает следующее: если обозначить через sl пересечение 92Р3 П SaSi, то прямая Р293 проходит через s[. Но тогда s, = 92Р3 П Р29з = Sp Значит, si лежит на S2S3, что и требовалось доказать.

6. Классические аксиомы трехмерного проективного пространства и проективной плоскости. Классическое трехмерное проективное пространство определяется как множество, элементы которого называются точками, снабженное двумя системами подмножеств, элементы которых называются соответственно прямыми и плоскостями. При этом должны выполняться следующие аксиомы.

Ть Две разные точки принадлежат единственной прямой.

Т2. Три разные точки, не лежащие на одной прямой, принадлежат единственной плоскости.

Тз. Прямая и плоскость имеют общую точку.

Т4. Пересечение двух плоскостей содержит прямую.

Т5. Существуют четыре точки, не лежащие в одной плоскости и такие, что любые три из них не лежат на одной прямой.

Те. Каждая прямая состоит не менее чем из трех точек.

Классическая проективная плоскость определяется как множество, элементы которого называются точками, снабженное системой подмножеств, элементы которой называются прямыми. При этом должны выполняться следующие аксиомы.

П]. Две разные точки принадлежат единственной прямой. Пг. Пересечение двух прямых непусто. Пз. Существуют три точки, не лежащие на одной прямой. П4. Каждая прямая состоит не менее чем из трех точек.

Множества P{L), где L -линейное пространство над полем J5f размерности 4 или 3, вместе с системами проективных плоскостей и прямых в них, как они были введены выше, удовлетворяют аксиомам Ti-Тб и ill-П4 соответственно, что немедленно следует из стандартных свойств линейных пространств, доказанных в ч. 1. Однако не всякое классическое проективное пространство или плоскость изоморфно (в очевидном смысле слова) одному из наших пространств P{L). Следующая фундаментальная конструкция дает много новых примеров.

7. Линейные и проективные пространства над телами. Телом (или не обязательно коммутативным полем) называется ассоциативное кольцо С, множество ненулевых элементов которого образуют группу по умножению (не обязательно коммутативную). Все поля являются телами, но обратное неверно. Например, кольцо классических кватернионов является телом, но не полем.

Аддитивная группа L вместе с бинарным законом умножения Ky.L-L: (а, /)н->а/ называется (левым) линейным пространством над телом К, если выполнены условия определения п. 2 § 1 ч. 1. Значительная часть теории линейных пространств над полями почти без изменений переносится на линейные пространства над телами. В частности, это относится к теории размерности и базиса и теории подпространств, включая теорему о размерности пересечения. Это позволяет построить по каждому телу К и линейному пространству L над ним проективное пространство P{L), состоящее из прямых в L, и систему его проективных подпространств Р{М), где McL пробегает линейные подпространства разных размерностей. Когда dim = 4 или 3, эти объекты удовлетворяют всем аксиомам Ti-Те и lli-П4 соответственно.

8. Роль теоремы Дезарга. Оказывается, однако, что существуют классические проективные плоскости, не изоморфные даже никакой плоскости вида P{L), где L - трехмерное линейное пространство над каким-нибудь телом. Причина этого состоит в том, что в проективных плоскостях вида P(L) теорема Дезарга по-прежнему верна, тогда как существуют недезарговы плоскости, где она не выполняется. Сформулируем без доказательства следующий результат:

9. Теорема. Три свойства классической проективной плоскости равносильны:

а) В ней выполняется плоская теорема Дезарга.

б) Ее можно вложить в классическое проективное пространство,

в) Существует линейное трехмерное пространство L над некоторым телом К, определенным однозначно с точностью до изоморфизма, такое, что наша плоскость изоморфна P{L).

Импликация б)=>а) устанавливается прямой проверкой того, что доказательство пространственной теоремы Дезарга использует лишь аксиомы Ti-Те. Импликация в) б) следует из того, что L можно вложить в четырехмерное линейное пространство над тем же телом.

Наконец импликация а)=*-в), являющаяся самым тонким моментом доказательства, устанавливается прямой конструкцией тела по дезарговой проективной плоскости. Именно, сначала с помощью геометрической конструкции проекций из центра вводится понятие проективного отображения проективных прямых в плоскости. Далее, доказывается, что для двух упорядоченных троек точек, лежащих на двух прямых, существует единственное проективное отображение одной прямой в другую. Наконец, фиксируется прямая D с тройкой точек ро, ри Рг, множество К определяется как D\{p2} с нулем ро и единицей pi, и законы сложения и умножения в К вводятся геометрически с помощью проективных преобразований. В проверках аксиом тела существенно используется теорема Дезарга, в этом контексте возникающая как аксиома Дезарга П5.

10. Роль теоремы Паппа. Даже в дезарговых плоскостях теорема Паппа может не выполняться. Назвав соответствующее утверждение аксиомой Паппа Пе, мы можем сформулировать следующую теорему, которую мы также приведем без доказательства:

И. Теорема, а) Если в классической проективной плоскости выполнена аксиома Паппа, то плоскость является дезарговой.

б) Дезаргова классическая плоскость удовлетворяет аксиоме Паппа тогда и только тогда, когда связанное с ней тело коммутативно, т. е. эта плоскость изоморфна P{L), где L - трехмерное линейное пространство над полем.

Дальнейшие подробности и опущенные нами доказательства читатель может найти в книге: Хартсхорн Р. Основы проективной геометрии. - М.: Мир, 1970.

§ 10. Кэлерова метрика

1. Если L -унитарное линейное пространство над С, то нл проективном пространстве P(L) можно ввести специальную метрику, называемую кэлеровой в честь открывшего ее важные обоб щения Э. Кэлера. Сама эта метрика была введена в прошлом веке Фубини и Штуди. Она играет особенно важную роль в комплексной алгебраической геометрии и неявно также в квантовой механике, потому что такие пространства P{L), как было объяснено в ч. 2, являются пространствами состояний квантовомеханнческих систем.

Эта метрика инвариантна относительно тех проективных преобразований P{L), которые имеют вид P{f), где f - унитарное отображение L в себя. Вводится она следующим образом. Пусть Рь Р2Р{Е). Точкам Ри р2 отвечают два больших круга на еди-

ничной сфере S cz L, как показано в разделе в) п. 3 § 6. Тогда кэ-лерово расстояние d{pi, рч) равно расстоянию между этими кругами в евклидовой сферической метрике 5, т. е. длине кратчайшей дуги большого круга на S, соединяющей две точки на прообразах р1 и Р2.

Основная цель этого параграфа - доказательство следующих двух формул для d{pu рч).

2. Теорема, а) Пусть h.kL, ;i = ;2=I; puPiP(L) - прямые C/i и С/г. Тогда

rf(pi,P2)==arccos(/i,/г),

где (li, la) -скалярное произведение в L.

б) Пусть в L выбран ортонормированный базис, относительно которого в P{L) определена однородная система координат. Пусть две близкие точки р\, ргеР(£) заданы своими координатами (уи Уп) и {у1-{- dyy, уп-h dyn) в аффинной карте Uo {см. раздел а) я. 3 § 6). Тогда квадрат расстояния между ними с точностью до третьего порядка малости по dyi равен

Доказательство, a) В евклидовом пространстве расстояние между двумя точками на единичной сфере равно длине той дуги соединяющего их большого круга, которая лежит между О и л, т. е. евклидову углу, или арккосинусу евклидова скалярного произведения радиусов. Евклидова структура на L, отвечающая исходной унитарной структуре, задается скалярным произведением Re(/i, h). Поскольку мы должны найти минимальное расстояние между точками больших кругов (еЩ\), (еЩ), а арккосинус - убывающая функция, нужно подобрать ф и if так, чтобы при данных h, h величина Re{e/i, е'*/г) приняла наибольшее возможное значение. Но она не превосходит h) \ и при подходящих ф, i) достигает этого значения: если ф = -arg{/, 1%), то {efl\, 1ч) - - ({/ь /г) . Поэтому окончательно

d{Pu P2) = arccos(/ /г).

б) Положим

/ п Ч1/2 / п \1/2

R=-[l + Y\yi?) . R + dR = [\-\-Y\yi + dytfj .

Тогда прообразами точек {уи уп) и {у\-\-dyx,... ,уп-{-dyn) на 5 будут точки

А lA 1 ( ) + Уп + уЛ

~V? R Р J 2 \p + dR- R-i-dR--- R-\-dRj