щейся также многогранником. Если S ограничен, f принимает свое максимальное значение в некоторой вершине S.

Доказательство. Проведем индукцию по размерности А, Случай dim Л = О очевиден. Пусть dim Л = п и для меньших размерностей теорема доказана. Пусть 5 задан системой неравенств fiO, /т 0. Так как множество S замкнуто, ограниченная сверху функция f на нем принимает максимальное значение в некоторой точке а. Если fi{a)>0, fm(a)>0, то по лемме п. 6 / мойсет быть только константой; в частности свое единственное значение она принимает на всем S. Иначе fi{a) = 0 для некоторого i. Это значит, что / принимает максимальное значение в точке непустого многогранника 5,-, который является гранью 5 и лежит в аффинном подпространстве {a\fi{a)=0} размерности п-1, ибо /( непостоянна. По индуктивному предположению максимальное значение ограничения / на принимается во всех точках некоторой многогранной грани Si. По лемме п. 4 она же будет гранью S. Она будет многогранником, ибо к неравенствам, определяющим ее в Si, с левыми частями, продолженными на все Л, следует добавить равенство fi = 0.

Теперь индукцией по размерности аффинной оболочки S покажем, что у любого ограниченного многогранника обязательно есть вершина. В самом деле, для размерности нуль это очевидно. Пусть размерность больше нуля. Мы можем считать, что аффинная оболочка S есть все Л. Возьмем любую непостоянную аффинно линейную функцию на Л. Она должна принимать на S максимальное значение, ибо S ограничен и замкнут. Стало быть, у S есть непустая грань, во всех точках которой это значение принимается. Она является ограниченным многогранником, аффинная оболочка которого имеет строго меньшую размерность. По индуктивному предположению у нее есть вершина, являющаяся также вершиной S по лемме п. 6.

Окончательно, пусть S ограничен и 7 -многогранная грань S, на которой исходная функция f принимает свое максимальное значение. Тогда любая вершина Т, существование которой доказано, является искомой вершиной S.

§ 5. Аффинные квадратичные функции и квадрики

1. Определение. Квадратичной функцией Q на аффинном пространстве (Л, L) над полем Ж называется отображение Q: А^Ж, для которого существуют такие точка аое.-Л, квадратичная форма q: Ь^Ж, линейная форма I: Е^Ж и константа с е. Ж, что

Q{a) = q{a - ао) + / (а - Gq) + с

для всех а S Л.

Форма q назьшается квадратичной частью Q, а I- линейной частью Q относительно точки ао. Очевидно, c~Q{ao). Покажем прежде всего, что от выбора точки ао квадратичность Q не зависит. Точнее, пусть g - симметричная билинейная форма на L,

являющаяся поляризацией q. Мы, как обычно, считаем, что характеристика Ж отлична от двух.

2. Предложение. Если Q{a) = q{a -ао)-\-1(а - flo) + c, то для любой точки До е Л имеем

Q{a)=q{a-d,) + l{a-a,) + c,

где

I (т) = 1(т) + 2g(m, а' - а,), с'= Q {а',).

Таким образом, переход к другой точке меняет линейную часть Q и константу.

Доказательство. В самом деле,

9 ( - о) <7 {{а - а'о) + - Со)) =-

<7 ( - йо) + 2g {а - flo. < - о) + 9 ( о о). l(a-a,) = l({a-a,) + {a,-a,)) = l(a-a,) + l{a,-a,),

что доказывает требуемое.

3. Назовем точку ар центральной для квадратичной функции Q, если линейная часть Q относительно Со равна нулю. Объяснение этого термина состоит в замечании, что точка ао центральна тогда и только тогда, когда Q(a) = Q(ao -(а - flo)) для всех а: действительно, разность левой и правой части в общем случае равна 2/(а - ао), ибо q(a - aQ)=q{~{a - ао)). Геометрически это значит, что после отождествления Л с L, при котором ао переходит в начало координат, функция Q становится симметричной относительно отражения mi-*-т.

Назовем центром функции Q множество ее центральных точек.

4. Теорема, а) Если квадратичная часть q функции Q невырождена, то центр Q состоит из единственной точки.

б) Если q вырождена, то центр Q либо пуст, либо является аффинным подпространством в А размерности dim A - rkq (rk - это ранг q), направляюи{ее подпространство которого совпадает с ядром q.

Доказательство. Начнем с любой точки аоеЛ и представим Q в виде q(a - ао)+/(а - ао)+с. Согласно предложению п. 2 точка а' А будет центральной для Q тогда и только тогда, когда выполнены условия

l{m) - 2g(m, а' - а^)

для всех mmL. Когда а^ пробегает все точки Л, вектор а' - а^ пробегает все элементы L, и линейная функция от mL вида -2g{m, а'ц - а^ пробегает все элементы L*, лежащие в образе канонического отображения g\ L-L*, связанного с формой g.

Если q невырождена, то g - изоморфизм. В частности, для функционала - 2eL* имеется единственный вектора' - а^Ь со

свойством g( -, а' - а^) - - - / ( ) Точка а' в этом случае и

является единственной центральной точкой Q.

Если q вырождена, то возможны два случая. Либо -1/2 не лежит в образе g; тогда центральных точек нет. Либо -1/2 лежит в образе g. Тогда для любых двух точек а^, а с условием

имеем а' - а е Кег g, и наоборот, если g ( , а' - а^ = - -jI { ) и а еао+ Кег g, то

Таким образом, центр является аффинным подпространством, а Kerg, т. е. ядро q, - его направляющим. Это завершает доказательство.

Теперь мы можем доказать теорему о приведении квадратичной функции Q к каноническому виду в подходящей аффинной системе координат {ао, ей е„}, {е,} - базис L, а^еА. Напомним, что точка а е. А в ней представлена вектором (xj, Хп),

п

если a = ao+Exjej.

5. Теорема. Пусть Q -квадратичная функция на аффинном пространстве А. Тогда существует такая аффинная система координат в А, в которой Q принимает один из следующих видов.

п

а) Если q невырождена, то Q (л: . ., x )= Е + с: ki, се Ж.

б) Если q вырождена ранга t, но центр Q непуст, то

г

в) Если q вырождена ранга г и центр Q пуст, то

.....VHr+r

Доказательство. Если q невырождена, выберем в качестве ао центральную точку Q. Тогда Q{a) = q{a - ао)-\-с. В качестве еь ..., е„ выберем базис в L, в котором q приводится к сумме квадратов с коэффициентами. Тот же прием приводит к цели всегда, если центр непуст.

Если центр Q пуст, начнем с произвольной точки ао и базиса

г

{еь вп}, в котором квадратичная часть Q имеет вид YkfX.

Пусть линеЙ1!ая часть имеет вид / = Е ltXt- Мы утверждаем, что

Ui -ф О для некоторого / > г. Действительно, иначе < = У ц^х/, и

тогда Q можно представить в виде

Следовательно, точка а^ - -ge, будет центральной для Q, что

/=1

противоречит предположению о пустоте центра.

Но если ц/ > О для некоторого / > г, то система функционалов {е', е% /} в L* линейно независима. Мы можем дополнить ее до базиса в L* и в двойственном базисе L получить для Q вы-

г

ражение вида Е л:, + с, где Xr+i как функция на L есть

просто /. Теперь ясно, что имеется точка, в которой Q обращается в нуль, например, х\= ... = лгг == О, Хг+\ =-с, Хг+2 ... = -п == == О в этой системе координат. Начав построение с этой точки, мы

г

получим представление Q в виде /1+ r+i-

6. Дополнения, а) Вопрос о единственности канонического вида сводится к уже решенной задаче о квадратичных формах. Если q невырождена и в некоторой системе координат имеет вид

п

Е iX] -f с, то точка (0.....0) является центром и потому определена однозначно, константа с определена однозначно как значение Q в центре, а произвол в выборе осей и коэффициентов тот же, что для квадратичных форм. В частности, над R можно считать, что Я, = ±1, и полным инвариантом является сигнатура. Над С можно считать, что все Я,- = 1.

В вырожденном случае с непустым центром начало координат можно выбирать в центре как угодно, но константа с все равно определяется однозначно, ибо значение Q во всех точках центра постоянно: если а, ао лежат в центре, то 1{а~ао) = О и q{a~-ao) = = О, ибо а - ао лежит в ядре q. К квадратичной части применимы прежние замечания.

Наконец, в вырожденном случае с пустым центром начало координат можно брать в любой точке, где Q обращается в нуль; к квадратичной части применимы прежние замечания.

б) Если А - аффинное евклидово пространство, то Q приводится к каноническому виду в ортонормированном базисе. Числа Яь Я„ определены однозначно. Произвол в выборе центра тот же, что и в аффинном случае, произвол в выборе осей тот же, что для квадратичных форм в линейном евклидовом пространстве.

6. Аффинные квадрики. Афф|1нной квадрикой называется множество {ащА\Q(a) = 0}, где Q - некоторая квадратичная функция на А. Взгляд на канонические формы Q показывает, что к проблеме исследования типов квадрик применимы все результаты § 10 ч. 2.

Рассмотрим вопрос о единственности функции Q, задающей данную аффинную квадрику над полем R. Прежде всего, квадрика может быть аффинным подпространством в А (возможно, пустым):

уравнение Y х] - равносильно системе уравнений Xi= ... =i

... =х, = 0. При г > 1 имеется много непропорциональных друг другу квадратичных функций, задающих ту же квадрику, напри-

г

мер Yi-xi - O с любыми А,/> 0. Покажем, что для остальных

квадрик ответ проще:

7, Предложение. Пусть аффинная квадрика X, не являющаяся аффинным подпространством, задается уравнениями Qi = О и Qa = О, где Qi, Q2 - квадратичные функции. Тогда Qi - KQ2 для подходящего скаляра Я е R.

Доказательство. Прежде всего, X не сводится к одной точке. В силу предложения п. 18 § 3 имеются две точки а аг аффинная оболочка которых (прямая) не лежит в X целиком.

Пусть ai, огеА и прямая, проходящая через точки аи аг, не лежит в X целиком. Введем в А систему координат {аи ei, вп}, где еп==аг - а\. Запишем функцию Qi в этой системе координат

.....x )lxi + l[ (х,.....х„ ,) + (х,. .... х„ ,),

где / /[ - аффинно линейные функции, т. е. многочлены степени 1 от Xl, x -i. Так как прямая, проходящая через точки

ai =(0, 0) и а2 = (0.....О, 1), не содержится в X целиком,

то Я, 4 О и (0) - 4U (0) > 0. Разделив Q, на Я, можно считать,

что Я = 1. Аналогично, можно считать, что как квадратный трехчлен от х„:

и 4(0)-4/2(0) > 0. Мы знаем теперь, что Qj и Q2 имеют одинаковое множество вещественных корней, и хотим доказать, что Qi = Q2.

Фиксируем вектор (ci, c i)eR - и рассмотрим векторы {tci.....tCn-\), teR. При малых по модулю значениях t дискриминанты по Хп трехчленов Qi(tCu .... tCn-u Хп) и Qiitci.....<c i,

Хп) остаются положительными, и вещественные корни их, отвечающие точкам пересечения одной и той же прямой с X, совпадают.

Значит, /i = /2 и - в таких точках {tci.....tCn-\). Поэтому

и ибо аффинно линейные функции, совпадающие

на открытом множестве, совпадают. Действительно, их разность обращается в нуль в окрестности начала координат и потому множество ее корней не может быть собственным линейным подпространством. Это завершает доказательство.

§ 6. Проективные пространства

1. Аффинные пространства получаются из линейных забвением начала координат . Проективные пространства можно строить из линейных по меньшей мере двумя способами.

а) Добавить к аффинному пространству бесконечно удаленные точки .

б) Реализовать проективное пространство как множество прямых в линейном пространстве.

Мы выберем в качестве основного определения б): оно яснее показывает однородность проективного пространства.

2. Определение. Пусть L - линейное пространство над полем Ж. Множество P{L) прямых (т. е. одномерных линейных подпространств) в L называется проективным пространством, ассоциированным с L, а сами прямые в L называются точками РЩ.

Число dimL- 1 называется размерностью P{L) и обозначается dimP(L). Одномерные и двумерные проективные пространства называются соответственно проективной прямой или проективной плоскостью. Проективное пространство размерности п над полем Ж обозначается также ХР или Р (Х). или просто Р . Смысл соглашения dimP(L)= dimL- 1 станет сейчас ясен.

3. Однородные координаты. Выберем базис {cq, вп) в пространстве L. Каждая точка pP{L) однозначно определяется любым ненулевым йектором на соответствующей прямой в L. Координаты Хо, ..., Хп этого вектора называются однородными координатами точки р. Они определены с точностью до умножения на ненулевой скаляр: точка {Ixq, Ххп) лежит на той же прямой р и все точки прямой получаются таким образом. Поэтому вектор однородных координат точки р по традиции обозначается {xq- Xi: ... :хп).

Таким образом, координатное п-мерное проективное пространство Р(Ж +) есть множество орбит мультипликативной группы Ж* = Ж\{0}, действующей на множестве ненулевых векторов Х +\ {0} по правилу Я(хо, ...,Хп) = (1хо,Кхп); (xq: ху:... :х„) есть символ соответствующей орбиты.

Пользуясь однородными координатами, можно хорошо представить себе структуру Р как множества несколькими разными способами.

а) Аффинное покрытие Р . Положим

ff = {(o: .х„)\х1фО}, г = 0, .... п.

п

Очевидно, Р = и Ui. В классе векторов проективных координат

любой точки р е Ui имеется единственный вектор с 1-й координа-220

той, равной 1: (хо: ... :xt: ... :Xn) = {xo/xi: ... :1: ... Опу-

ская эту единицу, получаем, что Ui биективно множеству Х , которое мы можем интерпретировать как п-мерное линейное или аффинное координатное пространство. Заметим, однако, что пока у нас нет никаких оснований считать, что на Ui имеется какая-то естественная не зависящая от выбора координат линейная или аффинная структура. Позже мы покажем, что инвариантно можно ввести на Ui лишь целый класс аффинных структур, связанных, впрочем, каноническими изоморфизмами, так что геометрия аффинных конфигураций в любой из них будет одна и та же.

Назовем множество Ui X i-u аффинной картой Р (в данной

системе координат). Точки (j/< .....y)eUi и (у\\ y>)eU,

при 1Ф] отвечают одной и той же точке Р , лежащей на пересечении Uif\Ui, тогда и только тогда, когда, вставив 1 на t-e место в векторе (у[\ .... и на /-е место в (t K .... мы полу-

чим пропорциональные векторы.

В частности, Р' = (7oU Ui, Uo = V\ Ж; точка yeUo отвечает точке \/yeU\ при у фО; точка г/ = О из Со не лежит в Ui, а точка 1/у = 0 из Ui не лежит в Uq. Естественно считать, что Р' получается из f/o = X добавлением одной точки с координатой у=оо. Обобщая эту конструкцию, получаем

б) Клеточное разбиение Р . Положим

Vi = {{xa: ... :хп)\х,==0 при ]<i, Х1ФО}.

п

Очевидно, Vo = Uo и Р = U Vi, но на этот раз все Vi попарно

не пересекаются. В классе проективных координат любой точки peVi имеется единственный представитель с единицей на t-м месте; опуская эту единицу и предшествующие нули, мы получаем биекцию Vi с Ж -К Окончательно

Р Ж иЖ -[}Ж -[] ... и Ж'Ж []P ~.

Иными словами, Р получается добавлением к Uo = Ж бесконечно удаленного (п-1)-мерного проективного пространства, состоящего из точек {0:xi: ... :x ); в свою очередь, оно получается из аффинного подпространства Vi добавлением бесконечно удаленного (относительно Vi) проективного пространства Р - и т. д.

в) Проективные пространства и сферы. В случае X = R или С есть удобный способ нормировки однородных координат в Р , не требующий выбора ненулевой координаты и деления на нее. Именно, любую точку Р можно представить координатами {хо: ...

х„) с условием Jjxif=l, т. е. точкой на п-мерной (при

Ж-R) или (2п-}-1 )-мерной (при Ж=С) евклидовой сфере. Степень оставшейся неоднозначности такова: точка (Яхо: ... :Ях ) по-прежнему лежит на единичной сфере тогда и только тогда, когда Я|= 1, т. е. Я==±1 при X=-R, К = е'% О < ф < 2я при Х = С.

Иными словами, n-мерное вещественное проективное пространство RP получается из п-мерной сферы S отождествлением пар ее диаметрально противоположных точек. В частности, RP устроена как окружность, а RP -как лист Мёбиуса, к которому по его границе приклеен круг (рис. 1, 2).

Сложнее увидеть CP : в одну точку CP склеивается целый большой круг сферы 5 +, состоящий из точек {хое'ч>, х„е'ч>) с переменным ф. Из описания CP в случае б) в качестве С U {оо} ясно, что CP можно представлять себе как двумерную сферу Ри-мана, в которой оо представлена северным полюсом, как при сте-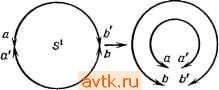

Рис. 1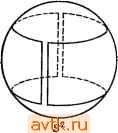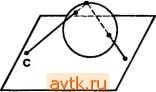

Рис. 2

Рис. 3

реографической проекции (рис. 3). Поэтому наше новое представление CP в виде факторпространства дает замечательное отображение SS, слои которого являются окружностями S. Оно называется отображением Хопфа.

В описании этого пункта мы совсем забыли о линейной структуре, исходной для RP и CP , зато нам стали ясно видны топологические свойства этих пространств, в первую очередь их компактность. (Строго говоря, в определении Р никакая топология не фигурировала; удобнее всего вводить ее именно с помощью отображений сфер, условившись, что открытые множества в RP и CP это те, прообразы которых в 5 и 5 + открыты.) Впредь мы не будем пользоваться топологией и вернемся к изучению линейной геометрии проективных пространств. Не будет, однако, преувеличением сказать, что важность RP и CP в значительной мере объясняется тем, что это естественные ком-пактификации R и С , позволяющие распространить основные черты линейной структуры на бесконечность. Даже над абстрактным полем X, не несущим никакой топологии, эта компактность

проективных пространств появляется в массе алгебраических вариантов. Типичный пример: на аффинной плоскости две разные прямые, вообще говоря, пересекаются в одной точке, но могут быть и параллельны. Это означает, что точка их пересечения ушла в бесконечность , и при переходе в проективную плоскость она благополучно обнаруживается: любые две проективные прямые на плоскости пересекаются.

Вернемся теперь к систематическому изучению геометрии Р

4. Проективные подпространства. Пусть Mcz L - любое линейное подпространство в L. Тогда P(M)cz: P(L), ибо каждая прямая лежащая в М, является в то же время прямой, лежащей в L.

Множества вида Р{М) называются проективными подпространствами в P{L). Очевидно, P(Mi П 2) = P(Ali)n Р(Л12), и то же верно для пересечения любого семейства. Следовательно, семейство проективных подпространств замкнуто относительно пересе-> чений. Поэтому в множестве проективных подпространств P(L), содержащих данное множество SczP{L), имеется наименьшее - пересечение всех таких подпространств. Оно называется проектив ной оболочкой S, обозначается S и совпадает с Р(М), где М-г линейная оболочка всех прямых, отвечающих точкам seS, в L

При переходе от пар LczM к парам P{L)czP{M) размерности уменьшаются на единицу, так что коразмерность dimL -dimM совпадает с коразмерностью dim P(L)-dim Р(М). Далее, как мы уже отмечали, P(Mi П Л^2) = P(Ali)n Р(Л^2), а PiMyMi) совпа-. дает с проективной оболочкой P(Mi)UP(M2).

Пользуясь этими замечаниями, мы можем написать проективный вариант теоремы п. 3 § 5 ч. 1. Заметим лишь, что в соответствии с определением в п. 2 размерность пустого проективного пространства следует считать равной -1: этот случай вполне реален, ибо непустые подпространства могут иметь пустое пере- сечение.

5. Теорема. Пусть Pi, Р2 - два конечномерных проективных подпространства в проективном пространстве Р. Тогда

dim Pi П Р2 + dim Pi U Р2 = dim P, + dim Pg.

6. Примеры, a) Pi, P2 - две разные точки. Тогда dimPinP2= - I, dim Pi = dim P2 = 0, откуда dim P, U P2 = 1, т. e. проективной оболочкой двух точек является прямая. Согласно определению проективной оболочки, она является единственной проективной прямой, проходящей через две точки.

б) Допустим, что dim Pi -f- dim P2 dim P. Тогда, поскольку dim Pi и 2 = dim P, имеем dim Pi П 2 < 0. Иными словами, два проективных подпространства, сумма размерностей которых больше или равна размерности объемлющего пространства, имеют непустое пересечение. В частности, в проективной плоскости нет параллельных прямых: любые две прямые пересекаются либо в одной точке, либо в двух и тогда (в силу примера а)) совпадают. Аналогично, две проективных плоскости в трехмерном проективном

пространстве обязательно пересекаются по прямой или совпадают. Проективная плоскость и прямая в трехмерном пространстве пересекаются по точке или прямая лежит в плоскости.

в) Условие Pif\P2 = 0 в случае Pi = P{Mi) означает, что Ml П = {0}, т. е. что сумма Mi + М2 прямая.

7. Задание проективных подпространств уравнениями. Линейная функция /: па линейном пространстве L не определяет Никакую функцию на P{L) (кроме случая fO), ибо всегда есть прямая в L, на которой эта функция непостоянна, и нет возможности фиксировать ее значение в соответствующей точке P{L). Но уравнение f О определяет линейное подпространство в L и потому проективное подпространство в Р(Х). Если L конечномерно, то любое подпространство в L и потому любое подпространство в P{L) можно задать системой уравнений

В однородных координатах Р этот эффект проявляется так: система линейных однородных уравнений

aijXf = G, t=l, m,

задает проективное подпространство в Р , состоящее из точек, однородные координаты которых {xq. Хп) удовлетворяют этой системе. Умножение всех координат на Я не нарушает обращения в нуль левых частей.

8. Аффинные подпространства и гиперплоскости. Пусть MczL - линейное подпространство коразмерности единица. Тогда P(M)cz c:P(L) имеет коразмерность единица, и мы будем называть такие лодпространства гиперплоскостями.

Мы покажем сейчас, как ввести на дополнении Ам к гиперплоскости Р(М) структуру аффинного пространства {Ам, М, -f). Выберем в L линейное многообразие М' = т' + М, не проходящее через начало координат. Оно имеет естественную аффинную структуру: сдвиг на m е М в М' индуцирован сдвигом на m в L, т. е. состоит в прибавлении т.

С другой стороны, Ам и М' находятся в биективном соответствии: точка Ам есть прямая, не лежащая в М, и она пересекается с М' в единственной точке, которую и поставим в соответствие исходной точке Ам- Так получаются все точки по одному разу. С помощью этого биективного соответствия аффинную структуру на М' можно перенести на Ам. Однако выбор М' не однозначен, и это приводит к неоднозначности аффинной структуры Ам. Чтобы сравнить две такие структуры, покажем, что тождественное теоретико-множественное отображение Ам в себя является аффинным изоморфизмом этих двух структур.

9. Предложение. Пусть {Ам, М, -{-) и {Ам, М, + ) - две аффинные структуры на Ам, построенные с помощью описанной конструкции. Тогда тождественное отображение Ам в себя явля-