

 |
 |
|
Разделы
Публикации
Популярные
Новые
|
Главная » Одинаково ориентированные векторы 1 ... 15 16 17 18 19 20 21 ... 31 = det / = 4 ((Я + nf - Я^ - ц ) = 4 {{Тг If - Тг Р) - (Z. О. Теперь очевидно, что {со, Ci, Сг, Сз} является ортонормированным базисом Ж с матрицей Грама diag(l,-1,-1,-1), так что сигнатура нашей метрики равна (1,3). Это завершает доказательство. 4. Следствие. Пусть LczJt - времениподобная прямая. Тогда с метрикой - (/, т) является трехмерным евклидовым пространством, и Ж - L@L. Доказательство. Утверждение Ж = L® следует из предложения п. 2 § 3, ибо времениподобные прямые, очевидно, невырождены. Так как сигнатура метрики Минковского на Ж есть (1,3), а на - (1,0), на она должна быть (0,3), что завершает доказательство. Перейдем теперь к изучению геометрического смысла скалярных произведений. Неопределенность метрики Минковского приводит к замечательным отличиям от евклидовой ситуации, которые имеют важный физический смысл. Самые яркие факты связаны с тем, что неравенство Коши - Буняковского -Шварца для вре-мениподобных векторов оказывается обращенным в другую сторону. 5. Предложение. Пусть (/i,/i)>0, (/г,/2)>0, he Ж. Тогда ih.tifXlu /.)(/2. к)- Равенство достигается тогда и только тогда, когда h, k линейно зависимы. Доказательство. Прежде всего проверим, что квадратный трехчлен (th -f k, tU + к) всегда имеет вещественный корень /о. В матричной реализации Ж условие {к, к) > О означает, что det к > О, т. е. что к имеет вещественные характеристические корни одного знака, скажем, ег (-Ь1 или -1). Аналогично, пусть 81 -знак собственных значений к. Тогда при t---(е1ег)оо матрица tl\ + к имеет собственные значения, примерно пропорциональные собственным значениям h (ибо. Л-ЬН/г стремится к к), и их знак будет -ег, а при t == О матрица Ок -\- к==к имеет собственные значения знака ег- Следовательно, при изменении / от О до -(е1ег)оо собственные значения t[\-\-к проходят через нуль, и det{tk-\-k) обращается в нуль. Значит, дискриминант этого трехчлена неотрицателен, так что {/,. /2)>(/l. /l)(/2. к)- Если он равен нулю, то некоторое значение toeR является двукратным корнем, и матрица tok + к, имея два нулевых собственных значения и будучи диагонализируемой (она эрмитова!), равна нулю. Поэтому к и к линейно зависимы. 6. Следствие ( неравенство треугольника в обратную сторону ). Если к, к времениподобны и {к,к) О, то к + к времениподобен и \к + к\>\к\+ \к\ [где / = {/,/)), и равенство достигается тогда и только тогда, когда 1\, k линейно зависимы. Доказательство. /,+/2p = /lP + 2{/ k)+\l2f> >/,Р + 2/, /2l + /2p = {Ull + /2lf. Равенство достигается лишь при (/), /2) = /i /2. Дадим теперь физические интерпретации этих фактов. 7. Парадокс близнецов . Времениподобные векторы h, h с (/i, к) О назовем одинаково временно ориентированными. Из предложения п. 5 видно, что для них /г) > 0. Вообразим двух близнецов-наблюдателей: один инерциален и движется по своей мировой линии от точки О до точки /) + /г, другой доходит до той же точки от начала отсчета, двигаясь сначала инерциально от О до /] и затем от h до 1\ + h: вблизи нуля и вблизи h он включает двигатели своего космического корабля, чтобы сначала улететь от брата, а затем снова вернуться к нему. Согласно следствию п. 6 собственное время, протекшее для путешествующего брата, будет строго меньше времени, протекшего по часам домоседа. 8. Множитель Лоренца. Если U и /г времениподобны и одинаково временно ориентированы, то по предложению п. 5 Ул!, > I м I I 2 I I, И МЫ не можем интерпретировать эту величину как косинус угла. Чтобы понять, что она собой представляет, снова прибегнем к физической интерпретации. Пусть /, 1=1, /2=1; в частности; инерциальный наблюдатель /) прожил единицу собственного времени с момента начала отсчета. В точке 1\ физическое пространство одновременных событий для него есть 1\ +(R/i)--. Мировая линия наблюдателя К/г пересекает это пространство в точке х/г.где х находится из условия {х/г-/ /,) = 0, т. е. л; = (/i,/г) . Расстояние от h до xh пространственнопо-добно: для наблюдателя Ш\ - это расстояние, на которое R/g удалился от него за единицу времени, т. е. относительная скорость R/2. Она равна (учесть, что у метрики в (R/i)- - следует изменить знак!) f = [ - (х/г ~ и, хк - h)V = [ - (хк - к, Х1,)УР = = [-х' (/г, /г) -f X (/,. = [ - (/,. 1Г' + iV\ Это знаменитый мнооюитель Лоренца; часто его пишут в виде -L, явно указывая, что скорости измеряются по отношению к скорости света. В частности. т. е. в момент собственного времени единица для первого наблюдателя второй наблюдатель находится в его физическом пространстве, когда часы второго наблюдателя показывают д/! ~ Это - количественное выражение эффекта сокращения времени для движущегося наблюдателя, качественно описанное в предыдущем пункте. 9. Евклидовы углы. В пространстве (R/o)--, где k - времени-подобный вектор, геометрия евклидова, и там скалярное произведение имеет обычный смысл. Пусть /i,/г -еще два времениподоб-ных вектора с той же ориентацией. Мы можем спроектировать их на (R/o)- - и вычислить косинус угла между проекциями. Предоставляем читателю самостоятельно убедиться в том, что для наблюдателя Шо это - угол между направлениями отлета от него наблюдателей Ш\ и R/2 в его физическом пространстве. Абсолютного значения этот угол не имеет; другой наблюдатель R/ увидит его другим. 10. Четыре ориентации пространства Минковского. Пусть (ei), е^}, i - 0, 3, - два ортонормированных базиса в J(-[e, е^ = =(е^, е'д)=1, (е^, e) = {e, е^) = - 1 при i == 1, 3. По аналогии с прежними определениями назовем их одинаково ориентированными, если один переводится в другой непрерывной системой ызо-метрий f: ЖJ[, 0</<1, /o = id, (е^) = е'. Два условия одинаковой ориентированности, очевидно, необходимы: а) (е^, бц) > 0. Действительно, [е^, (ef 1 по предложению п. 5, так что знак (ео, ft (ео)) не может меняться при изменении t, а (ео,/о(ео))= 1. Выше мы назвали е^ и е^ с таким свойством одинаково временно ориентированными. б) Определитель отображения ортогональной проекции ЕКб^- -Re, записанного в базисах {ej или {е[}, положителен. Действительно, проекция Е К^г Е ft {i) невырождена ни при каком значении t: иначе пространственноподобный вектор из Е был бы ортогонален Е R/ (е^) = {J (ео))-*- т. е. пропор- циоР1ален f (с,) - времениподобному вектору;это невозможно. Значит, определители этих проекций при всех / имеют одинаковый знак, а прп / = О он положителен. Можно сказать, что пары базисов со свойством б) одинаково пространственно ориентированы. Наоборот, если два ортонормированных базиса в Ж имеют одинаковую пространственную и временную ориентацию, то они одинаково ориентированы, т. е. переводятся друг в друга непрерывной системой изометрий ft. Чтобы построить ее, положим прежде всего {e) = , ---; Из условия {e, еЛ > 1 I 10 + u ~ ) 0 I следует, что ft (во) времениподобен и имеет квадрат длины единица при всех 0/1. Далее, в качестве ft(е\, 62,63) выберем ортонормированный базис в ft(eo), получающийся из проекции {е\,е2,ез} на ft(eo) процессом ортогонализации Грама - Шмидта; очевидно, он непрерывно зависит от t. Ясно, что f, (е^) = е', а {fi (fii), f 1 (eg). /1 (3)} и {e[, e, e суть одинаково ориентированные ортонормированные базисы в {е'. Их можно перевести друг в друга непрерывным семейством чисто евклидовых вращений (ео) . оставляющих е' неподвижным. Это завершает доказательство. Обозначим через Л группу Лоренца, т. е. группу изометрии пространства Ж, или 0(1,3). Пусть далее Л| - подгруппа Л, сохраняющая ориентацию некоторого ортонормированного базиса; - подмножество Л, меняющее его пространственную, но не временную ориентацию; - подмножество Л, меняющее его временную, но не пространственную ориентацию; - подмножество Л, меняющее его временную и пространственную ориентации. Нетрудно убедиться, что от выбора исходного базиса эти подмножества не зависят. Мы доказали следующий результат: И. Теорема. Группа Лоренца Л состоит из четырех связных компонент: Л = Л:: U U Л;}; U Л^ Тождественное отображение лежит, очевидно, в Л^. Аналогом теоремы п. 12 § 11 является следующий результат. 12. Теорема, Реализуем Ж как пространство матриц Грама эрмитовых метрик в Ж в базисе {Аь/гг}. Для любой матрицы V е SL (2, С) поставим в соответствие матрице I е Ж новую матрицу s(V)l = V4V. Отображение s определяет сюръективный гомоморфизм SL (2, С) на с ядром {± Е^. Доказательство. Очевидно, что s(y)l линейно по / и сохраняет квадраты длин: det(y/F)= det/. Поэтому s(F)eA. Так как группа SL(2, С) связна, любой ее элемент можно непрерывно деформировать в единичный, оставаясь внутри SL(2, С),- преобразование Лоренца s{V) можно непре'рывно деформировать в тождественное, так что s (У) е Л;. Поскольку s(id)=id и s(ViV2) = s{V\)s{V2), s является гомоморфизмом групп. Если у*ф = 1 для всех 1Ж, то, в частности, У'с,Г = С/, где оо = Eg, Oi, 02, 0Г3 - матрицы Паули. Условие VV = E2 означает, что V унитарна; после этого условия Vo,V - VOi{V*)- = oi означает, что У = ±£2: это было доказано в п. 12 § 11. Таким образом, Кег S = {±2}. Осталось установить, что s сюръективен. Пусть f: М-М - преобразование Лоренца из Л^, переводящее ортонормированный базис еД в \е'. Метрики на Ж, отвечающие и е определены, ибо собственные значения как ео, так и е^ имеют одинаковый знак, потому что det е^ - det е^ = 1. Из (е^, e ) > О следует, что эти метрики одновременно положительно или отрицательно определены. Действительно, выше мы убедились, что соединяющий их отрезок /еу+(1 -/Сц), 0/ 1, целиком состоит из временипо-добных векторов. Отсюда уже вытекает существование такой матрицы VeSL(2, С), что переводит е^ в е^, т. е. е'-У/е^ где ер и е^ отождествлены с их матрицами Грама. Действительно, V - это матрица изометрий (,9, е^) с (Ж, е^); априори ее определитель может быть равен -1, но это противоречило бы возможности соединить V с £2 в SL(2, С) с помощью деформации Vгде eo=(l/)f(eq)V,/ - соответствующая деформация в Л^. Итак, s(V) переводит е^ в е^. Дальше остается показать, что евклидов поворот \s{y)e, s(F)e2, s{y)e в {е[, Cj, е' можно осуществить с помощью s([/), где V е SL(2, С) и s(t/) оставляет ео на месте. Можно считать, что е представлен матрицей Оо в базисе {/ii.ftz}- Тогда мы должны выбрать V унитарной с условием t/(s{l/)e)L~ = e для t - 1, 2, 3. Это можно сделать по теореме п. 12 §11, ибо 6a3HCbi{s{F)eJ и {е^}, i=l, 2, 3, в (ео)- -ортонормированы и одинаково ориентированы. Доказательство окончено. 13. Евклидовы повороты и бусты. Пусть е^, е'-два одинаково временно ориентированных'времениподобных вектора длины единица, Lq, Lq - ортогональные дополнения к ним. Имеется стандартное преобразование Лоренца из Л^, переводящее во в е^, которое в физической литературе называется бустом. При е^е^ это - тождественное преобразование. Приец=7 оно определяется так: рассмотрим плоскость (Z. П о)- -. Она содержит е^ и е^. Сигнатура метрики Минковского на ней равна (1, 1). Поэтому существует пара единичных пространственноподобных векторов e, е[е (Lj,nLp)-L, ортогональных к е^, и е^ соответственно. Буст оставляет на месте все векторы из Lq(]Lq и переводит е^ в е', е, в е' соответственно. Чтобы вычислить элементы матрицы перехода {е^ е,} ( = {ер, е^}, заметим прежде всего, что с = (e, e) = = . * , где V - скорость относительного удаления инерциаль-ных наблюдателей, отвечающих и е^. Далее, матрицы Грама К. i} и , <} суть (J °). поэтому а2-б2 1 ac-bd = 0, c-d-l. Из первого уравнения, зная а, находим Ь = , -. Добавляя VI - v сюда условие, что определитель буста ad - be равен единице, получаем d = а, с = Ь. Окончательно, матрица буста в базисе {во, ei, е2, ез}, где {£2,3}-ортонормированный базис (Lf\Lj, имеет вид Vl -t)- Vl - г' V 1 о о о о О 0 10 о 0 0 1 или в терминах пространственно-временных координат Xq + Vxi VXq + х\ 0 -viTTiir x, X , Xr, x . Стоящую в левом верхнем углу матрицу можно записать также как матрицу гиперболического поворота / ch е sh е \ V sh е ch е j найдя е из условий che= -е shG: Если исходить из двух одинаково ориентированных ортонорми-рованных базисов {е„, е е^, е^ и (е^, е\, е', е', то преобразова-нне Лоренца, переводящее один в другой, можно представить в виде произведения буста, переводящего е^ п е', н затем евклидова поворота в (ео) который переводит образ базиса {е\, е-, ез} после буста в базис \е\, е', £3}, оставляя eJ- на месте. 14. Пространственные и временные отражения. Любое трехмерное подпространство LczJ(, на котором метрика Минковского (анти) евклидова (т. е. прямая L- - временнподобна), определяет преобразование Лоренца, тождественное на Z, и меняющее знак на L. Все такие операторы называются отражениями времени. Любое трехмерное подпространство Z, с на котором метрика Минковского имеет сигнатуру (1,2) (т. е. прямая простран-ственноподобна), также определяет преобразование Лоренца, тождественное на Z, и меняющее знак на L. Все такие операторы называются пространственными отражениями. Если фиксировать какое-нибудь отражение времени Т и пространства Р, то все элементы изЛ^, Л^*;, будут получаться из элементов умножением на Т, Р, РТ соответственно. 180 § 13. Симплектические пространства 1. В этом параграфе мы будем рассматривать конечномерные линейные пространства L над полем Ж характеристики Ф2, снабженные невырожденным кососимметрическим скалярным произведением [ , ]: LX L-Ж, и называть их симплектческими пространствами. Напомним свойства симплектических пространств, которые уже были установлены ранее, в § 3. Размерность симплектического пространства всегда четна. Если она равна 2г, то в пространстве существует симплектический базис [е\, ег\ Cr+i, е^г), т. е. базис с матрицей Грама вида / О В частности, все симплектические пространства одинаковой размерности над общим полем скаляров изометричны. Подпространство L[cz L называется изотропным, если ограничение скалярного произведения [, ] на него тождественно равно нулю. Все одномерные подпространства изотропны. 2. Предложение. Пусть L - симплектическое пространство размерности 2г, Ll а L - изотропное подпространство размерности г\. Тогда rir, и если ri < г, то L\ содержится в изотропном подпространстве максимальной возможной размерности г. Доказательство. Поскольку форма [,] невырождена, она определяет изоморфизм L -v L*, при котором вектору / е L ставится в соответствие линейный функционал /v->[/, /]. Отсюда следует, что для любого подпространства Lic L имеем dim L = = dim L - dim Lj (cp. § 7 ч. 1). Если к тому же изотропно, то L[ cz L, откуда r ----- dim dim L = dim L-dim = 2r-r, так что ri r. Рассмотрим теперь ограничение формы [, ] на L{-. Во всем пространстве L ортогональное дополнение к L/- имеет размерность dim L - dim Lf- - dim jL, ho предыдущему рассуждению. С другой стороны, L\ лежит в этом ортогональном дополнении и потому совпадает с ним. Значит, Li есть в точности ядро ограничения [, ] на Lf. Но в Lf- имеется симплектический базис в том его варианте, который рассматривался в § 3, где допускались вырожденные престранства: {ei, Сг-п', г-п-ц, вцг-пУ, в2{г-г,)+\.....е2г-г). с матрицей Грама
Размер единичной клетки есть -(dimLf - dimL,) = г - г ,. Векторы е2(г-1-1Н1. е^г-г, порожда[ют ядро формы naLf.T. е. добавив к ним, например, ei, er-r получим г-мерное изотропное подпространство, содержащее Lj. 3. Предложение. Пусть L ~ симплектическое пространство размерности 2г, Li с Z. - изотропное подпространство размерности г. Тогда существует ёругое изотропное подпространство Lg с /- размерности г такое, что L = Lj Ф Lg, и скалярное произведение индуцирует изоморфизм L.,-L\. Доказательство. Мы докажем несколько более сильный результат, полезный в приложениях, а именно установим существование подпространства Lg среди конечного числа изотропных подпространств, связанных с фиксированным симплектическим базисом {ei, ..., вг; е^+ь ..., егг} в L. Именно, пусть дано разбиение {1, ..., г}= / у/ на два непересекающихся подмножества. Тогда г векторов {е/, Cr+j i е /, / е /} порождают г-мерное изотропное подпространство в L, называемое координатным (относительно выбранного базиса). Очевидно, их имеется 2 Покажем, что L2 можно найти среди координатных подпространств. Пусть М натянуто на {е\, вг) и dim(Li [\М) - s, О s г. Существует такое подмножество /с:{1, г} из г - s элементов, что L\{\M трансверсально к N, натянутому на {ejte/}, т. е. Li [\M[\N = {{)}. Действительно, множество {базис Li{\M}\} U{ei, вг) пороА^дает М, поэтому базис Li[\M можно дополнить до базиса М с помощью г - s векторов из [е\, вг) по предложению п. 10 § 2 ч. 1. Номера этих векторов образуют искомое /, ибо Li П Л1 -f = М, так что Li П Л1П = {0}. Положим теперь /={1, г}\/ и покажем, что изотропное подпространство Lg, натянутое на {е,-, ег+,-11 е/, /е/}, является прямым дополнением к Li. Достаточно проверить, что Lin2 = {0}. Действительно, из доказательства предложения п. 2 следует, что Lj- = L, Lf = Lg. Но Li[\M содержится в L\, N содержится в L2, так что сумма М = L П М + ортогональна к Li П 2- Но М изотропно размерности г, поэтому М- - = М, и Lj П 2 с: М. Значит, окончательно Lin = (L,nM)n(L2nM) = (L,nM)nAf = {0}. Линейное отображение L,-yL\ ставит в соответствие вектору / е Lg линейную форму ть- [/,/п] на L\. Оно является изоморфизмом, ибо dim Lg = dira L = г, a его ядро содержится в ядре формы [,], которая, по предположению, невырождена. Это завершает доказательство. 4. Следствие. Любые пары взаимно дополнительных изотропных подпространств в L одинаково расположены: если L = LQL2 = = L[®L2, то существует изометрия f: L-L такая, что /(L,)= = L;, f(Lg) = L. Доказательство. Выберем базис {е\, ..., вг} в Li и двой-С1 венный к нему базис {вг+и .... гг} в L2 относительно описан- ного выше отождествления Li-Li. Очевидно, {ей бгг} есть симплектический базис в L. Аналогично построим симплектический базис {gj.....е2г} ° разложению LL. Линейное отображение f : е,. h-s-е^, i=l, 2г, очевидно, является требуемой изометрией. Из этого следствия и предложений пп. 2, 3 следует, что любые изотропные подпространства одинаковой размерности в L переводятся одно в другое подходящей изометрией. 5. Симплектическая группа. Множество всех изометрий f: L-*-L симплектического пространства образует группу. Множество матриц, представляющих эту группу в симплектическом базисе {еь егг}, называется симплектической группой и обозначается Sp(2r,X), если dim L = 2л. Условие /4sSp(2r,X) равносильно тому, что матрица Грама базиса {ej.....е2г}А совпадает с /2г== = ( £ 0*) - AhrA = lir, так что deti4 = ±1;ниже мы докажем, что dety == 1 (см. п. 11). Поскольку /3 = -гг условие можно записать также в виде А - -/2г(Л')~/2г. Отсюда вытекает 6. Предложение. Характеристический многочлен Р(0== = det(/£2- - Л) симплектической матрицы Л возвратен, т. е. Доказательство. Имеем, пользуясь тем, что dot Л = 1, del {lEir - Л) = det {tEir + Ir {AVhr) = det {tEr - (Л') ) = = det {tA* - Er) = det (Г'fjr - A*) = f det (/-£2, - A). 7. Следствие. Если Ж = R и A - симплектическая матрица, то вместе с каждым собственным значением X у А есть собственные значения Х-, Я и Я-. Доказательство. Поскольку Л невырождена, ХфО и Р(Я-) = Я~P(Я) = 0. Поскольку коэффициенты Р вещественны, Р(1) = Р(Я) = 0. Комплексное сопряжение есть симметрия относительно вещественной оси, а отображение Я>->Я- - симметрия относительно единичной окружности. Значит, комплексные собственные значения Л появляются четверками, симметричными одновременно относительно вещественной оси и единичной окружности, а вещественные собственные значения - парами. 8. Пфаффиан. Пусть Ж^ - координатное пространство, Л - невырожденная кососимметрическая матрица порядка 2г над Ж. Скалярное произведение [х, у] = х'Ау в Х^* невырождено и косо-симметрично. Переходя от исходного базиса к симплектическому, получаем, что для матрицы Л найдется такая невырожденная матрица В, что откуда det Л = (det В) 2. Итак, определитель каждой кососимметри-ческой матрицы является точным квадратом. Это наводит на мысль попытаться извлечь из определителя квадратный корень, который был бы универсальным многочленом от элементов А. Это действительно возможно. 9. Теорема. Существует единственный многочлен с целыми коэффициентами РГЛ от элементов кососимметрической матрицы А такой, что detЛ =(РГЛ)2 ы Pf( g ==1. Этот многочлен называется пфаффианом и обладает следующим свойством: Pf(BЛB)=detB Pf Л для любой матрицы В. (В случае сЪатЖфО коэффициенты Pf целы в том смысле, что лежат в простом подполе поля Ж, т. е. являются суммами единиц.) Доказательство. Рассмотрим г(2г-1) независимых переменных над полем Ж: {ац\ \ i <: j 2г}. Обозначим через К ноле рациональных функций (отношений многочленов) от atj с коэффициентами из простого подполя поля Ж. Положим А =(аг/), где а,7 = -Uji при а = О, и введем на координатном про- странстве К^ невырожденное кососимметрическое скалярное про- нзведенне х'Ау. Перейдя к симплектическому базису с помощью некоторой матрицы В, получим, как выше, det Л = (det 5) 2. Априори det В является лишь рациональной функцией от ац с коэффициентами из Q или простого поля конечной характеристики. Но так как det Л - многочлен с целыми коэффициентами, квадратный корень из него также должен иметь целые коэффи-цкенты (здесь мы пользуемся теоремой об однозначном разложении на множители в кольце многочленов Т[ац] или Fp[aiy]). Знак Vdet/l, очевидно, однозначно фиксируется требованием, чтобы значение Vdet/jr было равно единице. Последнее равенство из формулировки теоремы устанавливается так. Прежде всего, В'АВ кососимметрична вместе с А, так что РР (В'ЛВ) = det [В'АВ) = (det В) det Л = (det В) PF Л. Поэтому Pf {В*АВ) = ± det В PI А. Чтобы установить знак, достаточно выяснить его в случае А = J2r, В = Ечг, где он, очевидно, положителен. 10. Примеры. 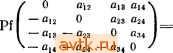 1 ... 15 16 17 18 19 20 21 ... 31 |
||||||||||||
|
© 2004-2025 AVTK.RU. Поддержка сайта: +7 495 7950139 в тональном режиме 271761
Копирование материалов разрешено при условии активной ссылки. |