где А-коэффициент усиления без обратной связи на низких частотах; f - рабочая частота; fi - граничная угловая частота или частота при 3 дБ, т. е. частота, на которой A{f) на 3 дБ иже Л, или равен 0,707Л.

Если, как это обычно бывает, /?н > У?вых, то fi = \/{2nRC), где /? = /?вых усилителя; С - паразитная емкость монтажа плюс мкость переходов в полупроводниках.

Обычно зависимость коэффициента усиления по напряжению от частоты дается в рационализованной форме'):

\A{!)\==AllT+mj, e==-arctg(f ,). (4.1)

Отметим еще раз, что f есть переменная, которая представляет интересующую нас частоту, в то время как fi - фиксированная частота, которая называется граничной или сопрягающей частотой и является характеристикой конкретного усилителя. Напомним, что сопрягающая частота f\ определяется как частота, на которой коэффициент усиления данного усилителя по напряжению падает до 0,707 от коэффициента усиления по напряжению на низких частотах, или, что то же, становится ниже Л на 3 дБ. Можно видеть, что увеличение частоты приводит к увеличению знаменателя в выражении для Л| (4.1) и, следовательно, к падению коэффициента усиления по напряжению.

Кроме того, из выражения для О (4.1) видно, что при изменении частоты фаза выходного сигнала сдвигается относительно фазы входного, причем величина сдвига фазы равна arctg( /i). Знак минус перед правой частью выражения для О означает, что выходной сигнал отстает по фазе от входного. Чтобы понять это, заметим, что сигнал проходит через усилитель не мгновенно, а задерживается на некоторое небольшое время как в активных (усилительных) элементах самого усилителя, так и под действием других внешних емкостей. При этом увеличение сдвига фазы с ростом частоты происходит даже в случае, когда время задержки для всех частот одинаково. Действительно, в этом случае время задержки составляет большую часть периода для сигнала большей частоты, что соответствует большему сдвигу фазы для более высокочастотных сигналов.

Вывод выражения (4.1) приведен в приложении В.

4.2. ШКАЛА ДЕЦИБЕЛ

В разд. 4.1 отмечалось, что при составлении графиков частотных характеристик используется логарифмический масштаб.

Как зависимость модуля усиления А и фазового угла 9 от частоты е. используется показательная форма представления А{}). - Прим. ред.

Приведем определение коэффициента усиления по напряжению в децибелах:

Коэффициент усиления по напряжению в децибелах = -:Л(дБ) = 201дЛ, где Л - числовое значение коэффицента усиления по напряжению.

Пример 4.1. Найти коэффициент усиления но напряжению в децибелах для усилителя с числовым значением коэффициента усиления, равным 10:

А (дБ) = 20 Ig 10 = 20 1 = 20 дБ.

В дальнейшем будем использовать обозначения Ig для логарифма по основанию 10 и 1п для натурального логарифма (по основанию е).

В табл. 4.1 приведены числовые значения коэффициента усиления по напряжению и соответствующие им величины в децибелах. Заметим, что, если

коэффициент усиления меньше единицы, его величина в децибелах отрицательна. Теперь можно, используя правила действий с логарифмами, переписать в децибелах выражение (4.1):

А (дБ) = 20 Ig Л - 20 Ig [1 -f (fIfiYf .

(4.2)

Рассмотрим случаи, соответствующие трем различным значениям частоты: случай 1, когда / < случай 2, когда f = fi; случай 3, когда f > fi.

Случай 1: f < fi! f лежит значительно ниже граничной частоты.

А (дБ) = 20 Ig Л - 20 ig [14- (f/Urf\

но f < f поэтому (flfiy 0; следовательно, [1 + (f/fiVV 1 20Ig 1 =0.

Таблица 4.1. Коэффициент усиления по напряжению и его значение в децибелах

Таким образом, Л (дБ) Случай 2: f = f,.

201gЛ, если f < U-

А (дБ) = 20 Ig Л - 20 Ig [1 + {flfxY\

= 20 Ig Л - 20 Ig V2 = = 20 Ig Л -20-0,15 =

= Л(дБ)-ЗдБ.

Таким образом, при f - U коэффициент усиления падает на 3 дБ по сравнению с коэффициентом усиления иа низких частотах, а сдвиг фазы 6 = = -45° (поскольку arctg 1 = 45°).

Случай 3: f > fi; f значительно превышает угловую частоту.

Л (дБ) = 20 Ig Л - 20 Ig [1 -f (f/f,)=]/l

Если f > и, то > 1 и [l-b {flUYVk fifu поэтому Л (дБ) = 201gA-

ч-201g(f/fi); легко видеть, что эта величина стремится к нулю при f- -/cp).

Если начертить графики зависимостей А (дБ) от частоты и фазового сдвига 6 от частоты, то получатся две кривые, аналогичные показанным на рис. 4.3. Рз этих графиков также видно, что сдвиг фазы равен -45° при частоте fi (точка 3 дБ) и приближается к 90° на частоте fcp, т.е. той частоте, на которой коэффициент усиления усилителя равен 1, или О дБ.

) Автор фактически дает определение частоты среза /ср, на которой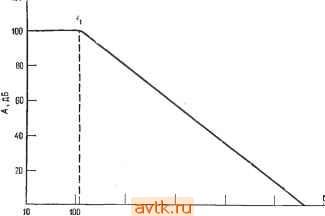

tOOO 10 кГц 100 кГц 1 МГц { 10 МГц

Частота , Гц

Частота, гц

100 1000 10 кГц 100 кГц 1 МГц 10 МГц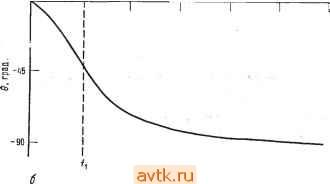

Рис. 4.3. Амплитудно-частотная и фазово-частотная характеристики операционного усилителя. а - зависимость коэффициента усиления -в децибелах от частоты; б - зависимость сдвига фазы от частоты.

4.3. НАКЛОН (СКОРОСТЬ СПАДА) КОЭФФИЦИЕНТА УСИЛЕНИЯ

Рассмотрим теперь скорость убывания коэффициента усиленияизображенной на рис. 4.4 эквивалентной схемы при увеличении частоты, когда частота превышает fi.

Уменьшение коэффициента усиления о частотой называется спадом. Спад вьшажается в децибелах на октаву или в децибелах на декаду. Октавой называется изменение (увеличение или

уменьшение) частоты вдвое. Например, если частота увеличивается от 500 до 1000 Гц, она возрастает на одну октаву. Декадой называется десятикратное увеличение или уменьшение частоты. Так, если частота увеличивается со 100 до 1000 Гц, она возрастает на одну декаду.

Посмотрим, что произойдет с коэффициентом усиления схемы на рис. 4.4, если частота изменится от fa до fb, причем /а > /и

Ua <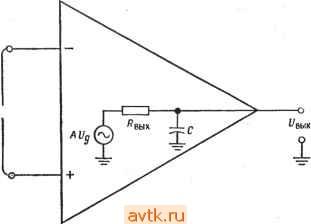

Рис. 4.4. Эквивалентная схема для расчета наклона частотной характеристики.

fb > fi И ffc > fa. Это изменение коэффициента усиления можно выразить следующим образом:

АЛ (дБ) = Л (дБ) при /(,-Л(дБ) при / =

= Л (дБ) - 20 Ig (/, ,) - [Л (дБ) - 20 Ig (/ /f,)] = = Л (дБ) - 20 ig (yf,) - Л (дБ) -f 20 Ig (Uf,) =

= 20 Ig ifjf,) - 20 Ig ifjfd = 20 ig (fjfb)

Если fb превосходит fa в 10 раз, то АЛ(дБ) = 201g(l/10) = =:201g0,l =-20 дБ. Таким образом, скорость спада для эквивалентной схемы на рис. 4.4 составляет 20 дБ/декада. Если теперь fb вдвое больше / , то АЛ (дБ) = 20 lg( 1/2) =-6 дБ. Итак, скорость спада для эквивалентной схемы на рис. 4.4 составляет 6 дБ/декада, что эквивалентно скорости спада 20 дБ/декада.

Укажем, что такая величина скорости спада характерна также для простых последовательных /?С-фильтров низкой частоты. На рис. 4.5 показана частотная характеристика усилителя, имеющего скорость спада 6 дБ/октава, или 20 дБ/декада. Проверьте

1 10 100 1кГц 10 кГц 100 кГц 1МГц 1 Ю 100 1 кГц 10 кГц 100 кГц 1МГ4 Частота, Гц частота, Гц

Рис. 4.5. Графики частотны.х характеристик, да- собственно частотная характеристика; б - аппроксимация частотной характеристики прямолинейными отрезками. Крутизна наклона характеристики составляет -6 дБ/октава или -20 дБ/декада. На частоте fi погрешность аппроксимации равна 3 дБ.

ЧТО на рис. 4.5 Л{дБ)= 80 дБ при f = 1 кГц и Л (дБ) = 60 дБ при / - 10 кГц, так что падение коэффициента усиления на ©дной декаде действительно составляет -20 дБ.

4.4. СКОРОСТЬ СПАДА

В МНОГОКАСКАДНОМ УСИЛИТЕЛЕ

Большинство операционных усилителей состоит из двух или более каскадов, каждый из которых имеет скорость спада € дБ/октава. Спад усиления многокаскадного усилителя имеет более сложную форму, чем спад, описанный в предыдушем разделе. Чтобы проанализировать ситуацию, будем использовать аппроксимацию амплитудно-частотной характеристики прямолинейными отрезками. Такие графики, на которых представлена зависимость десятичного логарифма коэффициента усиления от десятичного логарифма частоты, называются диаграммами Боде.

Рассмотрим трехкаскадный усилитель, показанный на рис. 4.6. Частотные характеристики его отдельных каскадов, графически показаны на рис. 4.7.

Обший коэффициент усиления всего усилителя - это произведение коэффициентов усиления его отдельных каскадов. В свою очередь, коэффициенты усиления этих каскадов имеют? Вид:

II + аЯп)] А

II + (f/fl2)]/ И.,

e = -arctg(f/f K е=-arctg (Ш. е--arctg (Ш.

где in есть /i каскада 1 усилителя; /12 - /1 каскада 2 усилителя; fi3 - /1 каскада 3 усилителя; лц - коэффициент усиления каскада 1 на низких частотах; л12 - коэффициент усиления каскада 2 на низких частотах; л,3 - коэффициент усиления каскада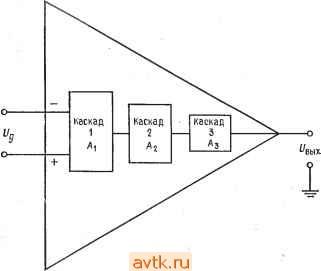

Рис. 4.6. Тре.хкаскадный операционный усилитель Свьш =

3 на низких частотах. Выражение для общего коэффициента усиления, учитывающее зависимость от частоты, имеет вид

Л Л,2Л1з

[1 + аппП [1 + [1 + ш/1з)=]/2.

е = - arctg (f/f ) - arctg (f ,) - arctg (Ш-

(4.3)

Выражением (4.3) пользоваться неудобно, поэтому для наглядного описания суммарной амплитудно-частотной характеристики будем использовать диаграммы Боде. Это оказывается значительно более удобным благодаря тому факту, что децибелы являются логарифмическими функциями и можно складывать значения коэффициентов усиления в децибелах вместо того, чтобы перемножать их числовые значения. Таким образом, для построения амплитудно-частотной характеристики всего усилителя надо на одном и том же графике начертить частотные характеристики отдельных каскадов и графически их сложить,

Обращаясь к рис. 4.8, видим, что на частотах ниже /ц общая частотная характеристика -это просто сумма коэффициентов усиления отдельных каскадов в децибелах, т. е. 30 дБ + 4- 20 дБ + 12 дБ = 62 дБ. В полосе частот между fu = 10 кГц и 1,2 = 40 кГц коэффициент усиления каскада 1 падает со скоростью 6 дБ/октава, в то время как коэффициенты усиления

Рис. 4.7. Диаграммы Боде отдельны.х каскадов усилителя, показанного на рис. 4.6.

а - частотная характеристика каскада 1. f = -10 кГц, fcp. 1=ЗМ кГц.

Спад коэффициента усиления равен 20 дБ/декада (6 дБ/октава); б - частотная характеристика каскада 2, f[2=*0 кГц, fcp.2=* кГц; Спад 20 дБ/декада (6 дБ/октава); в -частотная характеристика каскада 3.

ери

f,3 = r20 кГц, f

.=500 кГц.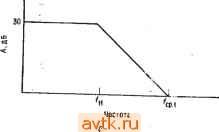

частота

Лз cp.s

каскадов 2 и 3 остаются постоянными. Поэтому общий коэффициент усиления, который на диаграмме Боде получается как сумма коэффициентов усиления трех отдельных каскадов, в этой полосе частот также падает на 6 дБ/октава. В полосе частот от fi2 = 40 кГц до fi3 = 120 кГц коэффициенты усиления каскадов 1 и 2 падают каждый со скоростью 6 дБ/октава, а коэффициент усиления каскада 3 остается постоянным на уровне 12 дБ. Следовательно, в полосе частот между /12 и /13 общий коэффициент усиления падает со скоростью 12 дБ/октава. В полосе частот между fi3 = 120 кГц и частотой fcp всего усилителя, равной 390 кГц, все три каскада имеют скорость спада по 6 дБ/ок-тава; следовательно, в этой полоев чаетот скорость спада

J I I f I ! 1 11

e цБ/октава (20 дБ/декада)

йБ/актава[АО дб/декада)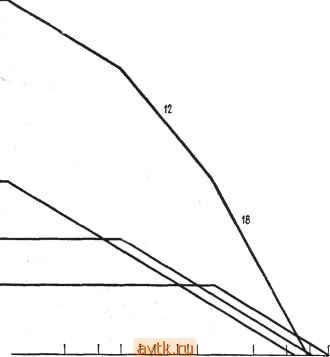

дБ/октава(60 дБ/декада)

JLLL

20 30 40 50 60 80 100 200 300 АСО 500 600 8001000

Частота, кГц

Рис. 4.8. Суммарная частотная характеристика последовательно соединенных каскадов, характеристики которых даны

на рис. 4.7.

Цифрами дт / ДР 4 обозиач^ни сдртветстренно суммарная характеристика и характеристики каскадов 1, 2 И 3i

Именно потому, что на частотах fu, fiz, fa происходит стыковка отдельных отрезков диаграммы Боде, оии и называются сопрягающими.- tipuM. ред.

трехкаскадного усилителя составляет 18 дБ/октава (или 60 дБ/декада)).

Этот метод анализа можно использовать для любого многокаскадного усилителя, если известны амплитудно-частотные характеристики его отдельных каскадов.

4.4.1. ФАЗОВО-ЧАСТОТНАЯ ХАРАКТЕРИСТИКА

Известно, что при прохождении через усилитель сигнал задерживается во времени и что для каждой конкретной частоты этой задержке соответствует запаздывание по фазе на некоторый угол. В выражении для коэффициента усиления в зависимости от частоты этот угол дается в виде -arctg(f/fi).

Из рис. 4.3 видно, что для отдельного каскада отставание по фазе равно 90° на частоте fcp- В многокаскадном усилителе каждый каскад последовательно увеличивает задержку, что приводит к увеличению суммарного запаздывания по фазе. Из выражения для суммарного коэффициента усиления (4.3) видно, что суммарное запаздывание по фазе выражается как

= -arctg if/и - arctg (f/h) - arctg (f/hz), (4.4)

если усилитель имеет, как в нашем примере, три каскада.

Из этого выражения видно, что максимально возможное запаздывание по фазе составляет -180° для двух каскадов и -270° для трех. Запаздывание по фазе для одного каскада не превышает 45° для частот, меньших сопрягаюшей частоты fi (/= fl, arctg 1=45°), и увеличивается до значений, больших 45°, когда / становится больше fi, приближаясь к максимальному значению (-90°) при частоте fcp-

4.4.2. ЧАСТОТНАЯ ХАРАКТЕРИСТИКА ПРИ НАЛИЧИИ ОБРАТНОЙ СВЯЗИ

До сих пор рассматривались частотные характеристики операционного усилителя в отсутствие обратной связи. Теперь проанализируем, какое действие на частотные характеристики оказывает обратная связь.

Добавление отрицательной обратной связи так, например, как это сделано в инвертирующем или неинвертирующем усилителях, увеличивает эффективную полосу пропускания операционного усилителя.

Чтобы убедиться в этом, рассмотрим выражение для коэффициента усиления без обратной связи усилителя со спадом

6 дБ/октава:

A{f)==A/[l+j{f/h)], (4.5)

где Л (f) -коэффициент усиления без обратной связи на частоте /; Л - коэффициент усиления без обратной связи на низких частотах; fi - сопрягающая частота. Подставляя (4.5) в выражение для коэффициента усиления при наличии обратной связи /С = Л/( 1 + ЛР), получим

К (f) = {Л/ [ I + / тШ 1 + И/[ 1 + / ( /.)]}=Л/11 + Р Л+iiflh)] ==

= [Л/(1+Лр)]/{1+/7/[/,(1+Лр)]}. (4.6)

Это выражение можно записать в виде

K{f)=KjV+iif/ho.c)h (4.7)

где /,о.с = fi(l + ЛР); /Ci - коэффициент усиления с замкнутой обратной связью на низких частотах; fio. с - сопрягающая частота при замкнутой петле обратной связи.

Выражение (4.7) показывает, что сопрягающая частота при наличии обратной связи равна сопрягающей частоте без обрат-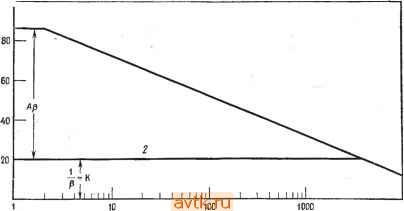

10000

Рис. 4.9. Влияние обратной связи на ширину полосы пропускания, у - частотная характеристика без обратной связи (спад 6 дБ/октава); 2 - частотная характеристика при наличии обратной связи. 1/(3 = C, <4Р -петлевой коэффициент уся-

леиня.

НОЙ связи, умноженной на петлевое усиление плюс единица. Поскольку при наличии обратной связи обычно (1 --ЛР)> 1, оказывается, что и fio. c>fi, так что эффективная ширина полосы пропускания действительно увеличивается при использовании обратной связи.

Чтобы понять это, обратимся к рис. 4.9. Пусть имеется усилитель с коэффщрентом уеиления без обратной связи, равным