тором полоса пропускания одного из этих фильтров перекрывается с полосой другого, является полосой пропускания всей-схемы.

. Схемы каскадов первого порядка, которые используются при-конструировании многокаскадных фильтров, показаны на

Рис. 8.21. Полосовой фильтр с широкой полосой, построенный

из фильтров верхних и нижних частот. а - частотвые характеристики; б - блок-схема полосового фильтра четвертого порядка: / - фильтры нижних частот второго порядка, 2 - фильтры верхних частот второго порядка.

рис' 8.22. Каждый из показ'анных на этом рисунке фильтров; имеет а = 1. Отметим, что полосовой фильтр первого порядка - это скорректированный дифференциатор.

пример 8.10. Построить фильтр нижних частот Баттерворта пятого порядка имеющий = 10 и Зд5 = 750 Гц и обладающий высокой стабильностью.

Для обеспечения хорошей стабильности в качестве отдельных каскадов следует использовать универсальные активные фильтры второго порядка. Блок-схема и электрическая схема фильтра, который мы собираемся построить, показаны на рис. 8.23.

Решение. Из табл. 8.2 находим значение а и отношение (коэффициент для fcp. каждого каскада:

: 1, коэффициент fcp= 1, 1,618, коэффициент /ср = 1. = 0,618, коэффициент /ср = Ь

Таким образом для каждого из каскадов /здБ = /ср

Каскад 1 Каскад 2 Каскад 3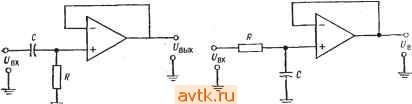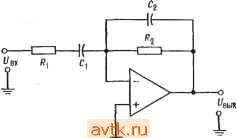

Рис. 8.22. Каскады первого порядка.

о-фильтр верхних частот, а = 1, fp = l/2nC; 6 -фильтр нижних частот, а=1; fpp=l/2n/?C; d-полосовой фильтр, а=1, f, = l/2nuC, f,=

в

Каскад первого порядка имеет К = I. Разделим желаемый коэффициент усиления поровну между двумя каскадами второго порядка. Имеем К2 =

= :д = д/,т.е./(2 = VlO = 3,16, = у 10 = 3,16. Так как /(заранее задан следует использовать универсальные активные фильтры с настраиваемым коэффициентом усиления.

Каскад 1. Положим С = 0,01 мкФ и найдем R:

R = 1/2л/срС = 1/2я (750 Гц) (0,01 мкФ) = 21,2 кОм.

Используем номинал 21,5 КОм ±2 %. Расчет каскада 1 окончен.

Каскад 2. Положим Ci = Сг = С = 0,01 мкФ, Так как R = = = = Ri = Rb = Ro. с = 1/2л/срС, С = 0,01 мкФ, R = 21,5 кОм, как и в первом каскаде. Найдем R4:

= ?о.с *Сп = 21,5 кОм/3,16 = 6,715 кОм.

Используем номинал 6,81 Юм ±2 %. Положим Ra = R к найдем Rb:

Rg = aR = 1,618 (21,5 кОм) = 34,8 кОм.

Используем номинал 34,8 кОм ±2%. Найдем ?нoмп:

?комп = /?з|/?о.с11 RARs-

=8,49 кОм.

Используем номинал 3,48 кОм ± 2 7о-

Так как напряжение сдвига последовательно усиливается во всех каскадах схемы, для уменьшения сдвига выхода инвертирующего усилителя следует-

каскад 1

Каскад 2 Pi,

каскад 3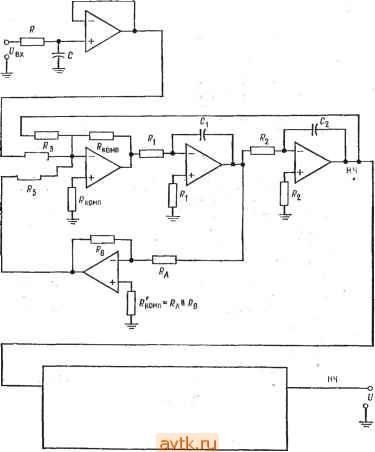

вык

Рис. 8.23. К примеру 8.10. Фильтр нижних частот Баттерворта пятого порядка.

о-блок-схема, / - каскад первого порядка, а = 1, fcp=f3 дБ- п~ 2-универсальный Фильтр второго порядка. о = 1,618, fcp = f3flB. Кп=3.6; 3 -универсальный фильтр второго порядка. а=0,618, [ср = ГздБ, K =S,\b. б-схема. Каскадм 2 и 3 идентичны, за исключением величин R и r .

d КОМП

222 Гтва 8

использовать сопротивление /?комп- Найдем его величину: комп = л11 в= 13.28 кОм

Используем номинал 13,3 кОм ±2 %. Расчет каскада 2 закончен.

Каскад 3. Так как каскад 3 отличается от каскада 2 только значением к, эти каскады идентичны во всем, кроме величин /?д и /?комп-Найдем Rb:

R = а/?д = 21,5 кОм (0,618).= 13,3 кОм

Используем номинал 13,3 кОм±2%. Найдем /? омп:

<омп = д11Лв = 8.21 кОм. Используем номинал 8,25 кОм ± 2 %.

Расчет каскада 3 закончен. Настройка а производится сопротивлением Rb каскада 3.

Пример 8.11. Построить фильтр верхних частот Чебышева шестого порядка, имеюший иеравиомериость 3 дБ и /з дб = Гц Чтобы проиллюстрировать использование схемы другого типа, в этом примере мы используем в качестве каскадов фильтра три схемы Саллеиа и Кея, реализуюшие фильтры верхних частот второго порядка.

Схема фильтра показана на рис. 8.24. Все каскады этой схемы выглядят одинаково. По отличаются друг от друга значениями параметров компонент, так, как/р =5 /з дб и различны в разных каскадах. Решение: Из табл. 8.2 находим:

I Каскад 1 а = 0,958, коэффициент fcp = 0,298,

\ Каскад 2 а = 0,289, коэффициент /ср = 0,722,

Каскад 3 а = 0,078, коэффициент fcp = 0,977.

Каакад 1. =/3 дз/(коэффициент fcp)=l кГц/0,298 = 3,356 кГц. Положим /?= У?, =/?2= л и С, = С2 = 0,01 мкФ Тогда /? = 1/2я;/срС = = 1/2я; (3,356 кГц) (0,01 мкФ) =4,74 кОм. Используем номинал 4,64 кОм ± ±2%. Найдем Рв:

= (2 - а) = (2 - 0,958) (4,64 кОм) = 4,83 кОм

Используем номинал 4,87 кОм ±2%. Найдем Кщ:

К у = (л+ RbIa) = (1 + 4.83 кОм/4,64 кОм) = 2,049. Каскад 2. /р =/3 дБ/(коэффициент /ср) = кГц/0,722 = 1,385 кГц.

Положим С = Ci = Сг = 0,01 мкФ и /? = /?, = /?j = R. Тогда R - = 1/2п/срС = 1/2я;(1,385 кГц) (0,01 мкФ) == 14,49 кОм. Используем номинал 14,7 кОм ±2%. Найдем Рв:

= (2 - а) /?д = (2 - 0,289) 14,47 кОм = 25,15 кОм

Используем номинал 24,9 кОм ±2%.

Найдем Km:

К„2 = 1 -Ь RblA= 1 + кОм/14,6 кОм = 2,69.

Каскад 3. fj,p = fa дБ/( оэффициент fp) = 1 кГц/0.977 = 1,024 кГц.

Положим С = С, = Cs = 0,01 мкФ и Л = y?i = = Лл. Тогда R = == 1/2я;/срС = 1/2л( 1,024 кГц) (0,01 мкФ) = 15,54 кОм.

Рис. 8.24. К примеру 8.11. Многокаскадный фильтр Саллена и Кея

шестого порядка, в каскаде 1: ci = c =0,01 мкФ, ri=ri= =Ra=W кОм, j?j3=4,87 кОм.

Б каскаде 2: Ci = c2=0,0I мкФ, j?,=j?2= =ra=li,7 кОм. rg=2i.9 кОм.

Б каскаде 3: Ci==c2=0,01 мкФ. j?, = i?2= = /?4= 15,4 кОм, J?j3=30,l kQm.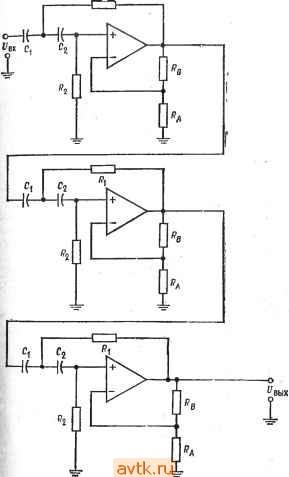

Используем номинал 15,4 кОм ±2%. Найдем Rb:

Лв = (2 - а) Лл = (2 - 0,078) 15,4 кОм = 29.6 кОм.

Используем номинал 30,1 кОм ±2 %. Найдем Каз и К^:

К„з=\+ RbIRa =1+30,1 кОм/15.4 кОм = 2,954, \Kj; = СтСпг^пЗ = (2.049) (2,69) (2,9б4) =- 16.28.

Это значение коэффициента усиления достигается на вершинах зубцов частотной характеристики фильтра, величина которых равна 3 дБ. Настройка (возможно, она окажется необходимой):

1) Величина неравномерности устанавливается с помошью сопротивления Rb каскада 3.

2) Частота устанавливается с помощью сопротивлений R\ и R2 каскада I.

8.7. ГИРАТОРЫ

Гиратор - это 7?С-цепь, включенная в обратную связь усилителя таким образом, чтобы имитировать катушку индуктивности. Иногда гираторы называют синтезируемыми индуктивности ми.

Использование схемы гиратора позволяет реализовать большую индуктивность в небольшом по размерам, легком и недорогом корпусе. Такие активные катушки индук-тивности могут быть использованы в некоторых классических типах фильтров вместо обычных катушек, что часто упрощает реализацию фильтров. Назначение гиратора состоит в том, чтобы, используя напряжение на конденсаторе, заставить напряжение и ток на входе схемы вести себя подобно напряжению и току в катушке индуктивности.

Основные недостатки гираторов заключаются в том, что, во-первых, только немногие из них могут работать на частотах, превышающих несколько килогерц, и, во-вторых, схемы гираторов, не требующие заземления одного из выводов, оказываются весьма сложными.

Чтобы понять, как действует гиратор, обратимся к рис. 8.25. Напомним, что ин.иуктивное сопротивление Xl при увеличении частоты возрастает, поэтому при возрастании частоты растет и напряжение на катушке индуктивности. Повторитель напряжения в схеме гиратора воспроизводит напряжение на сопротивлении Ri иа своем . выходе.. При увеличении частоты напряжение на конденсаторе С уменьшается вместе с Хс (емкостное сопротивление); следовательно, Ur а вместе с ним и L/вых ло-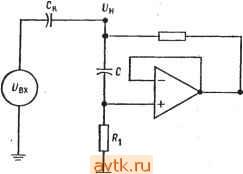

Рис. 8.25. Гиратор (схема Berndt и Dutta- Roy).

вторителя увеличиваются. Выходное напряжение повторителя через сопротивление R2 подается обратно на вход, поэтому напряжение на входном выводе схемы растет с увеличением частоты, т. е. ведет себя аналогично напряжению на катушке индуктивности. В этой схеме величину сопротивления следует выбирать как можно меньшей: чем меньше, тем лучше. Если в петле обратной связи гиратора последовательно с операционным усилителем включить токовый бустер и нагрузить его сопротивлением R2, то параметры всей схемы улучшатся.

8.7.1. РАСЧЕТ ГИРАТОРА

Выбрать R2 равным минимальному сопротивлению нагрузки данного операционного усилителя. Выбрать R\, удовлетворяющее условиям Rl > R2 (но не больше чем 200У?2) к Ri<. 0,1/?вх

Рис. 8.26. Пример гиратора.

операционного усилителя. Задать величину L. Используя соотношение

L = RiRrp, (8.25)

найти С: С = L/R1R2.

Добротность гиратора можно рассчитать по формуле

Ql2RxlR2

(8.26)

Пример 8.12. Построить, используя гиратор, последовательный /?/.С-контур, имеющий /о = 300 Гц. Соответствующая схема показана на рис. 8.26. Решение: Положим С, == 0,1 мкФ. Из соотношения найдем L =

= 1/4я;7оС;.= 1/4я;(300 Гц)(0,1 мкФ) = 2,8 Гн. Положим добротность катушки индуктивности Q равной 10 и выберем Ri; для операционного усилителя 741 y?2 = 1 кОм. Из соотношения Q = Vs VRi/2 найдем/?!: Л, = 2QRi = 2 (100) 1 кОм = 200 кОм.

Из соотношения L = RiRC найдем С:

С = LIR1R2 = 2,8 Гн/(1 кОм) (200 кОм) = 0,014 мкФ.

Если требуется большая точность, можно соединить параллельно два конденсатора, например 0,012 и 0,002 мкФ.

Если общая добротность схемы Q = 3, то R = Хс/(добротность схемы) = = 2п(вС/3 = 5,28 кОм/3 = 1,76 кОм. Используем номинал 1,78 кОм ± 2 %.

Если R слишком мало по сравнению с R2, то заданное значение Q окажется нереализуемым.

1. Активные фильтры применяются почти в любой отрасли электроники и потому заслуживают того, чтобы их изучать.

2. Хотя активные фильтры имеют много преимуществ перед пассивными, они имеют также и недостатки, к которым прежде всего относится ограничение максимальной рабочей частоты. (Есть надежда, что по мере усовершенствования операционных усилителей значение этого ограничения будет уменьшаться.)

3. Процедуры расчета активных фильтров не слишком сложны, даже если соответствующие схемы (например, схемы универсальных фильтров) выглядят сложными. Для полного проектирования активного фильтра необходимо рассчитать и чувствительности его параметров; соотношения, нужные для такого расчета, содержатся во многих книгах из числа перечисленных в конце этой главы.

4. Активные фильтры Саллена и Кея и фильтры с параллельной обратной связью -это простые схемы, на которые можно положиться, но по сравнению с более сложн{.1ми универсальными и биквадратными активными фильтрами они менее стабильны. Соединяя фильтры второго порядка (и фильтры первого порядка, если надо получить фильтр нечетного порядка), можно получать многокаскадные фильтры более высоких порядков. Процедура расчета многокаскадных фильтров скучна, но не сложна. Используя приведенные здесь методики, можно самостоятельно конструировать высококачественные активные фильтры.

ЛИТЕРАТУРА

!. Allen е.. Modern Techniques and Applications of Active Filters, Department of Electrical Engineering and Computer Science, Santa Barbara, Calif. 1974.

2. Berlin H. M., Design of Active Filters with Experiments, Howard W. Sams and Co., Indianapolis, Ind., 1977.

3. Hilbura J. L., Johnson D. E., Manual of Active Filter Design, McGraw-Hill, New York, N. Y., 1973.

4. Johnson D. E., Introduction to Filter Theory, Prentice-Hall, Englewood Cliffs, N. J., 1978.

5. Johnson D. E., Hilburn J. L., Rapid Practical Design of Active Filters, John Wiley and Son?, New York, N. Y., 1975.

6. Johnson D. E., Johnson J. R., Moore H. P., A Handbook of Active Filters, Prentice-Hall, Englewood Cliffs, N. J., 1980.

7. Lancaster D., Active Filter Cookbook, Howard W. Sams and Co., Indianapolis, Ind., 1975.

8. Toby G. E., Graeme J. G., Huelsman L. P., Operational Amplifiers, Design - and Application, McGraw-Hill, New York, N. J., 1971. [Имеется перевод: . ГрэмДж., Тоби Дж. Хьюлсман Л. Проектирование и применение операционных усилителей. Пер. с англ. - М.: Мир, 1979.]

9. Wong Yu Jen, Ott W. E., Function Circuits, Design and Application McGraw-Hill, New .York, N. Y., 1976.

КОНТРОЛЬНЫЕ ВОПРОСЫ

8.1. Назвать четыре преимущества активных фильтров перед пассивными.

8.2. Назвать два основных недостатка активных фильтров..

8.3. Начертить по памяти частотные характеристики фильтров нижних и верхних частот и полосового фильтра. Обозначить на этих рисунках полосу пропускания, полосу заграждения (подавления) и переходный участок.

8.4. Указать связь между числом полюсов активного фильтра и наклоном характеристики на переходгюм участке.

8.5. Перечислить преимущества каждого из следующих типов фильтров: Баттерворта, Чебыщева и Бесселя.

8.6. Указать связь между величиной коэффициента затухания к фильтра и его частотной характеристикой вблизи fcp.

8.7. Рассчитать схему Саллена и Кея с равными компонентами, реализующую фильтр нижних частот Баггерворта второго порядка с fg = 5 кГц. Положить С = 0,015 мкФ.

8.8. Рассчитать схему Саллена и Кея, реализующую фильтр верхних частот Баттерворта второго порядка с f.?дБ = 7 кГц. Положить С = 0,012 мкФ.

8.9. Рассчитать схему с параллельной обратной связью, реализующую полосовой фильтр второго порядка с fi == I кГц, = 1,2 кГц и Кп = Ь. Положить С = 0,0033 мкФ.

8.10. Рассчитать схему универсального фильтра с единичным усилением, реализующую фильтр верхних частот второго порядка. Фильтр должен иметь характеристику Чебыщева с неравномерностью 1 дБ, f з дб = Гц и С = = 0,001 мкФ.

8.11. Рассчитать схему универсального фильтра с единичным усилением, реализующую полосовой фильтр с /i = 1,1 кГц и fs = 1,15 кГц. Положить С = = 0,022 мкФ.

8.12. Рассчитать схему универсального фильтра с изменяемым коэффициентом усиления, реализующую фильтр нижних частот второго порядка. Фильтр должен иметь характеристику Чебыщева с неравномерностью 2 дБ, fздБ = = 2,5 кГц, С = 0,033 мкФ к Кп = 8.

8.13. Рассчитать схему универсального фильтра с изменяемым коэффициентом усиления, реализующую полосовой фильтр с fi = 500 Гц, /г = 525 Гц, Кп = = 10 и С = 0,01 мкФ.

£.14. Рассчитать биквадратный полосовой фильтр с fi = 740 Гц, Кп = 10 и С = 0,0047 мкФ.

8.15. Рассчитать фильтр нижних частот, имеющий характеристику Чебышева четвертого порядка с неравномерностью 2 дБ. В качестве каскадов использовать два фильтра Саллена и Кея второго порядка. Положить fз дб = 3 кГц и С = 0,0033 мкФ.

8.16. Указать значения а и коэффициента fcp для каждого из каскадов фильтра пропускания верхних частот восьмого порядка, имеющего характеристику Чебышева с неравномерностью 1 дБ.

8.17. Описать назначение гиратора.

8.18. Указать преимущества металлопленочных сопротивлений в активных фильтрах.

Если вы не можете ответить на некоторые из этих вопросов, отметьте их и еще раз просмотрите соответствующие разделы.

ЛАБОРАТОРНАЯ РАБОТА

Цели работы. После выполнения этой лабораторной работы студент Должен уметь рассчитывать величины компонентов, собирать и проверять частотные характеристики схем активных фильтров Саллена и Кея с параллельной обратной связью, универсальных и биквадратных.

Оборудование. I. Пять операционных усилителей цА741 фирмы Fairchild или им аналогичных. 2. Набор сопротивлений, имеющих точность 2 %. 3. Источник питания ±15 В постоянного тока. 4. Осциллограф с внещиим входом горизонтальной развертки. 5. Генератор качающейся звуковой частоты (при

Генератор качающейся частоты

fBbix

Выход Аналог Q частоты

исслед\емый фильтр

Осциллограф

Внешний горизонтальный о-Вертикальные вход входы -о Синх.1

-о I Синх.г

Рис. 8-27. Включение осциллографа для получения частотной характеристики.

отсутствии генератора качающейся частоты можно использовать звуковой сигнал-генератор). 6. Набор конденсаторов на металлизированном майларе, желательно с точностью ±5 7о. 7. Макетная панель, такая, как EL Instruments SK-10.

При выполнении этой работы используются процедуры расчета, приведенные в разд. 8.5.

Порядок выполнения работы. 1. Монтаж измерительной аппаратуры. Осциллограф и генератор качающейся частоты нужно соединить таким образом, чтобы график частотной характеристики исследуемого активного фильтра был виден непосредственно на экране осциллографа. Схема такого соединения показана па рис. 8.27. Напряжение на выходе Аналог частоты генератора качающейся частоты пропорционально частоте и линейно зависит от времени; оно используется для управления усилителем горизонтальной развертки осциллографа. При этом горизонтальная развертка изображает частоту, а амплитуда сигнала на экране осциллографа соответствует амплитуде па выходе фильтра. Полученное таким образом изображение частотной харак--