Решение: Из табл. 8.1 находим /здвДср>974; а = 0,886, поэтому /р = = /здб/1,074= 12 кГц/1,074 = 11,174 кГц. Положим С, =С2 = С = 0,001 мкФ

и Л = Л, = /?2 = 3=4=Ro. с = о. с- Тогда Л = 1/2л/срС = 1/2и X X (11,174 кГц) (0,001 мкФ) = 14,2 кОм. Используем номинал 14кОм±2%. Rb = 0. с (3/а - 1) = 14 кОм (3/0,886 - 1) = 33,4 кОм. Используем номинал 33,2кОм±2%.

Если в первом каскаде появляется заметный сдвиг, воспользуйтесь балансировочным соп[зотивлением Rx, подключив его, как показаЕЮ в схеме сложения-вычитания (гл. 5) разд. 5.3.

Замечание. Q = 1/а 1,13. Добротность полосового фильтра в данном случае оказывается равной 1,13, т. е. ее значение очень мало. Именно поэтому универсальный фильтр следует, как правило, использовать или как фильтр верхних и (или) нижних частот, или как полосовой фильтр, но не как оба фильтра одновременно.

Пример 8.6. Рассчитать компоненты схемы универсального фильтра с единичным усилением, реализующей полосовой фильтр. Фильтр должен иметь U = = 940 Гц и /г = 1 кГц.

Решение: /о = VfJs = V(940 Гц) (1 кГц) = 969,5 Гц, Q =/ /(/г -/,) = = 969,5 Гц/(1 кГц -940 Гц) = 16,15. Положим С, = Сг = С = 0,033 мкФ и

/? = /?, = 2 = Лз = /?4 = с = ro. с- Тогда R = 1/2п/оС = 1/2я (969,5 Гц) X X (0,033 мкФ) = 4,97 кОм. Используем номинал 5,11 кОм±2о/о-

= (3Q - 1) Ло. с = 13 (16,15) - 1] 5,11 кОм = 243 кОм. Используем номинал 237 кОм±2 %.

Сбалансируйте схему сложения - вычитания, если это окажется необходимым.

Кп = Q = 16,15.

Процедура расчета компонентов схемы универсального активного фильтра с изменяемым коэффициентом усиления

Как и в случае универсальных активных фильтров с единичным усилением, процедуры расчета схемы универсального активного фильтра с изменяемым коэффициентом усиления (рис. 8.17) идентичны для фильтров верхних и нижних частот, а для расчета схемы полосового фильтра служит отдельная процедура. Процедуры расчета для универсальных фильтров с изменяемым коэффициентом усиления. Фильтры верхних и нижних частот

1. По табл. 8.1 найти ./здбДср соответствующие выбранному типу фильтра. Если /здбДср= йти f.

2. Выбрать С=С, = С2 и R = Ry= R = Ro.c Ra, найти R no формуле /ср = 1 /2nRC.

3 По заданному Кп найти Rt. Так как Кп = Ro. c/Ri, Ri =

2 Яо- с/Кп.

4- Найти Rb по формуле

, RB = aRA. (8.16)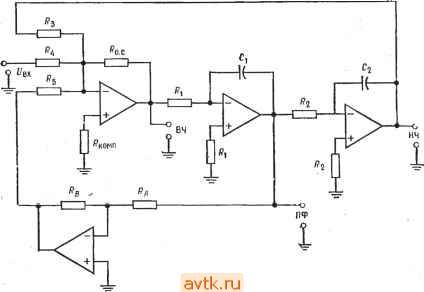

Рис. 8.17. Схема универсального активного фильтра второго порядка с изменяемым коэффициентом усиления. Обозначения ВЧ, НЧ и ПФ те же, что и на рис. 8.16.

Настройка: i

1) Установить а путем изменения Ra и,ли Rb. Установить Кл с помощью изменевия Ri. Установить /ср путем одновременного изменения Cj и или Ri и R2.

Процедура расчета для универсальных фильтров с изменяемым коэффициентом усиления. Полосовой фильтр

1. Выбрать /), /2 и Кп. Найти /о и Q по формулам /о --\ i/2. Q = fo/(f2-fi)< 150.

2. Найти G - коэффициент пропорциональности между Кп и Q. Так как

K = GQ, G = KJQ. (8.17)

3. Выбрать С = С, = С2. По,ложить R = Ri = R2 = R3 = R5 = = Ro.c = Ra и найти R no формуле R = l/2nfoC.

4. Найти Ri no формуле

RiRo.jG. (8.18)

5. Найти Rb no формуле

Rb = Ra/Q. (8.19)

Замечание. Если Rb < Usux/I вых. макс данного операционного усилителя, то надо увеличить Ra и повторить вычисление Rb-.

Пример 8.7. Рассчитать схему универсального фильтра с изменяемым коэфг фициентом усиления, реализующую фильтр верхних частот Баттерворта. Порядок фильтра равен двум, /ср = 1,5 кГц, Ка = 5. Решение: По табл. 8.1 находим ф/fcp - U а = 1,414.

Положим С = С, = Сг = 0,0063 мкФ и л = л| = лг = Лз == R?, = ло. с = = лд и найдем R:

R == l/2nfcpC = 1/2л (1,5 кГц) (0,0068 мкФ) = 15,6 кОм.

Используем номинал 15,4 кОм ± 2 %. Найдем Rb:

Rb = Л = 414 (15,4 кОм) = 21.8 кОм

Используем номинал 21,5 кОм ± 2 7о-Найдем R4:

Ri = Ro. cfKn = 15,4 кОм/5 = 3,08 кОм.

Используем оминал 3,01 кОм ± 2 %. Найдем Лкомп:

/?комп = Лз II ло. с II л* II лб = 1.934 кОм. Используем поминал 1,96 кОм ±2%.

Пример 8.8. Рассчитать схему универсального фильтра с изменяемым коэффициентом усиления, реализующую полосовой фильтр с / = 2,2 кГц, fi = = 2,3 кГц я Кп= 10.

Решение: / = V/iTi = V(2,2 кГц) (2.3 кГц) = 2,249 кГц, Q = /0/(2- - f,) = 2,249 кГц/(2,3 кГц -2,2 кГц) = 22,5, О == Ku/Q = 10/22,5 = 0,444. Положим С = С, = С2 = 0,0033 мкФ и л = л1 = лг = Лз = Л5 = Ro. с = лд и найдем л:

л = l/2nfoC = 1/2п (2,249 кГц) (0,0033 мкФ) = 21,44 кОм. -

Используем номинал 21,5 кОм ± 2 %. Найдем Rb:

Rb = Ra/Q = 2Ь55 кОм/22,5 = 956 Ом.

Используем номинал 953 Ом ± 2 %.

Замечание. Операционный усилитель 741 может работать на Нагрузку 953 Ом, хотя это близко к минимально допустимой величине лв. Найдем л :

Л4 = ло. с/О = 21,5 кОм/0,444 = 48,4 кОм.

, Используем номинал 48,7 кОм ±2%. Найдем Лкомп:

лкомп = Л5II лз 1! Л4II ло. с = 2,9 кОм. Используем номинал 2,87 кОм + 2%.

8.5.5. БИКВАДРАТНЫЙ ПОЛОСОВОЙ ФИЛЬТР

Процедура расчета показанной на рис. 8.18 схемы биквадратного полосового фильтра состоит в следующем:

1. Выбрать fu /2 и Кп. Вычислить fo и Q по формулам fo = Vf if2?

- Вычислить

G = Q/Kn- . . , (8-20)

3. Вычислить Ri и Rk по формулам

Ri = GI2nUC, RK = Q/2nhC. (8.21). (8.22)

4. Положить R = R2 = R3 = R4 = Rz и вычислить R по формуле R = 1 /2nfoC.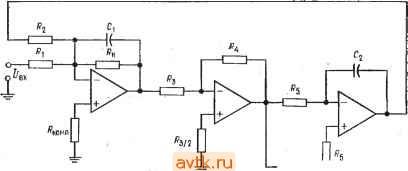

~ еых X

Рис. 8.18. Биквадратный полосовой фильтр.

Настройка:

1) Установить fo с помощью изменения R2.

2) Установить Q путем изменения Rk.

3) Установить Кп с помощью изменения

пример 8.9. Рассчитать биквадратный полосовой фильтр, имеющий f, = 97 Гц, /2 = 102 Гц и К. =J0.

Яеше не: / = Vf.b = V(102 Гц) (97 Гц) = 99,47 Гц. Q = (/2-/1) == = 99,47 Гц/5 Гц = 19,9, g = Q/Kn = 19,9/10 = 1,99.

Положим С = С, = = 0,047 мкФ и R = Rs = Ra = Ra Rs- Найдем R: R = 1/2л/оС = 1/2л (99,47 Гц) (0,047 мкФ) = 34 кОм.

Используем номинал 34,8 кОм ± 2 %.

Найдем R,:

Ri = G/2nfoC = 1,99/2л (99,47 Гц) (0,047 мкФ) = 67,7 Юм.

Используем номинал 68,1 кОм ±2 7о-Найдем Rk:

Rk = QI2nfoC = 19,9/2л (99,47 Гц) Г0,047 мкФ) = 677 кОм

Используем номинал 681 кОм ± 2 %. Для обеспечения баланса по токам смещения положим сопротивление на неинвертирующем входе операционного усилителя равным ?з/2 = 34,8 кОм/2 = 17,4 кОм и используем номинал 17,4 кОм ± 2 %. Найдем ?кoмп:

комп = II 1II = 21,9 кОм. Используем номинал 21,5 ±2 7о.

8.6. КАСКАДНОЕ СОЕДИНЕНИЕ ФИЛЬТРОВ

Если нужен фильтр с числом полюсов, большим двух, то его легко можно построить, соединив последовательно несколько фильтров более низкого порядка. В этом разделе объясняется, каким образом следует соединять активные фильтры для получения многокаскадных фильтров более высоких порядков.

8.6.1. КАСКАДНОЕ СОЕДИНЕНИЕ ДЛЯ ПОЛУЧЕНИЯ ХАРАКТЕРИСТИКИ БОЛЕЕ ВЫСОКОГО ПОРЯДКА

Соединяя каскадно фильтры первого и второго порядков, можно получить фильтр любого более высокого порядка. Как

Третий порядок

Четвертый порядок

Пятый порядок

стой порядок

ис. 8.19. Каскадное соединение фильтров первого и второго порядков дл получения фильтров более высоких порядков. ;- фильтры первого порядка, 2 - фильтры второго порядка.

ВИДНО ИЗ рис. 8.19, каскадное соединение фильтра второго порядка и фильтра первого порядка дает фильтр третьего порядка, а каскадное соединение двух фильтров второго порядка дает фильтр четвертого порядка. Увеличивая число соединяемых фильтров первого и второго порядков, можно получить фильтр любого нужного нам порядка. Фильтры нечетных поряд-

ков обычно строятся из фильтра первого порядка в качестве первого каскада и нескольких фильтров второго порядка в качестве остальных каскадов. Например, фильтр седьмого порядка строится из одного (первого) каскада первого порядка и трех каскадов второго порядка. Фильтры четных порядков строятся-лз п/2 каскадов второго порядка, где п - желаемый порядок

1.. первый порядок

2..

второй порядок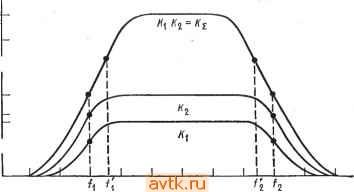

0.7U7/f£ I

0.5 К.

0.707 /fj

0,707 1 =

Частота

Рис. 8.20. Сужение полосы пропускания; f2 - 0,64/2, /J = l,55/i.

фильтра. Ввиду того что каскадное соединение приводит к сужению полосы пропускания, отдельные каскады многокаскадных активных фильтров не следует делать идентичными.

Чтобы понять, как происходит сужение полосы пропускания, рассмотрим рис. 8.20. Если каскадно соединить два фильтра первого порядка с коэффициентами усиления /Ci и /(2 и с одинаковой полосой пропускания, то полоса пропускания полученного двухкаскаД1;ого фильтра окажется более узкой, чем полоса пропускания каждого из каскадов. Действительно, на частоте и К\ = 0,707 (Ki в середине полосы) и /(2 = 0,707 (/Сг в середине полосы), поэтому на частоте /, общий коэффициент уси^ ления /Сх =/Ci/C2 = 0,5(/Cz в середине полосы), т. е. меньше чем 0,707 (/Сх в середине полосы). Аналогично на частоте /2 /Се = 0,5 (/Сх в середине полосы). Поэтому новое значение, .f[, при котором /(j, = 0,707 {Kj в середине полосы), лежит.

выше, чем /ь а новое значение f, при котором Kil = 0,707 (/Сх. ;в середине полосы), лежит ниже /2, т. е. новая полоса пропускания оказывается уже старой. Если включить каскадно п идентичных фильтров первого порядка, то верхняя частота среза /2 и нижняя частота среза f[ п-каскадного фильтра будут связаны с верхней /2 и нижней /1 частотами среза каждого из каскадов соотношениями

f2 = f2V2. (8-23)-

. f[ = fj2}i\. (8.24).

Эти соотношения относятся только к каскадам первого порядка, поэтому их нельзя использовать при расчете большинства многокаскадных активных фильтров, содержащих, как правило, каскады второго порядка. Однако эффект сужения полосы пропускания при каскадном соединении фильтров имеет место независимо от порядка каскадов.

Неравномерность характеристики многокаскадногс^ фильтра оказывается выше, чем неравномерность характеристики каждого из каскадов. Например, каскадное соединение двух фильтров второго порядка, имеющих каждый неравномерность характеристики 3 дБ, дает фильтр с неравномерностью 6 дБ, потому что Кх = КхК2 = КхШ + К2Ш.

Для получения наилучших результатов при конструировании многокаскадных фильтров оказывается необходимым использовать каскады с неодинаковыми значениями а и (если фильтр не является фильтром Баттерворта) /ср. Так, три каскада второго порядка в фильтре шестого порядка могут иметь одну и ту же схему, но величины некоторых из компонентов должны быть различными для разных каскадов.

Значения а и коэффициента /ср, которые следует использовать при конструировании многокаскадных фильтров, имеющих порядок от трех до восьми, даны в табл. 8.2. Использование этой таблицы поясняется несколькими примерами, которые приведены ниже в этом разделе.

В многокаскадных полосовых фильтрах обычно используется четное число каскадов. Если ширина полосы пропускания полосового фильтра больше чем (приблизительно) 50 % /о, то такой полосовой фильтр проще построить из фильтра верхних и фильтра нижних частот, соединив эти фильтры каскадно. Построенный таким образом полосовой фильтр четвертого порядка, будет состоять из двух фильтров верхних частот второго порядка и из двух фильтров нижних частот второго порядка (рис. 8.21). Укажем, что в такой схеме фильтр нижних частот Задает /2, а фильтр верхних частот - f\. Интервал частот, в ко-

Таблица 8.2. Параметры мйогокаскадных фильтров Фильтр Баттерворта

Фильтр Чебышева, неравномерность 0,5 дБ

Фильтр Чебышева, неравномерность 2 дБ

Порядок

Первый каскад

коэффициент

Второй каскад

коэффициент

Третий каскад

коэффициент

Четвертый каскад

коэффициент

0,976 0,983 0,797 0,842

0,070 0,054

0,987 0,990

Фильтр Чебышева, неравномерность 3 дБ

Порядок

Первый каскад

коэффициент

Второй каскад

коэффициент

Третий каскад

коэффициент

Четвертый каскад

коэффициент fcp

0,299 0,443 0,178 0,298 0,126 0,224

0,326 0,179

0,468 0,289 0,504 0,325

0,916 0.950 0,614 0.722 0,452 0.566

0.113 0,078 0.199 0,147

0,967 0,977 0.792 0,839

0,057 0,044

0,983 0.987

Фильтр Бесселя

Порядок

Первый каскад

коэффициент

Второй каскад

коэффициент

Третий каскад

коэффициент

Четвертый каскад

коэффициент

5 6 Г 8

1,916 1

1,959

- :1

-17976-

2,322 2,067 3,647 2.872

4-;9Г2 -37701

1,447

1,241

1,775

1.636

1,878 -

2,483 1,624 2,874 3,867

-3,562 41389

1,091 0,977

1,51-3 17407...

2.711 3.722

07637

- 4-7е&

- 5-;680

Замечание. Первый каскад всех фильтров нечетного порядка является фильтром первого порядка.

Для фильтров нижних частот: fcp=f3flB (коэффициент f(.p), где fcp=fcp используемой при вычислениях для одного-каскада.

для Фильтров верхних частот: jCp=f3 дБ/(крэффициент fp), где^здЕ - желаемое значение Зд5