СВЯЗИ обратно на вход сумматора и складывая его со входным напряжением всей схемы, можно осуществлять регулировку частотной характеристики вблизи частоты среза. Выходом соответствующего фильтра нижних частот является выход второго интегратора.

Характеристика фильтра верхних частот формируется посредством суммирования взятых в противофазе входного сигнала и сигнала с выхода фильтра нижних частот. На частотах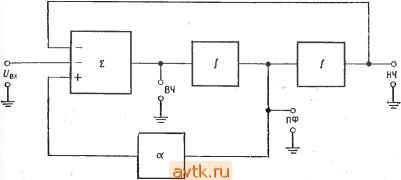

Рис. 8.10. Блок-схема универсального активного фильтра.

ВЧ - выход фильтра верхних частот, НЧ - выход фильтра нижних частот, ПФ - выход полосового фильтра.

ОТ нулевой и до fcp эти два сигнала взаимно уничтожаются, а на частотах выше fcp выходной сигнал фильтра нижних частот исчезает, что дает возможность входному сигналу беспрепятственно проходить через сумматор на выход фильтра верхних частот.

Сигнал на выходе полосового фильтра можно рассматривать как интеграл от суммы выходных сигналов фильтров пропускания верхних и нижних частот. Ослабление сигнала на выходе фильтра верхних частот уменьшается, когда частота сигнала приближается к fcp, а интегрирование обеспечивает ослабление на частотах выше fcp. Так как частота fcp одинакова для обоих интеграторов, сигнал на выходе может быть отличным от нуля только в случае, когда характеристики фильтров верхних и нижних частот перекрываются, как это показано на рис. 8.11. Если величина а= 1/Q мала, то Q=[/a велика, и тем самым обеспечивается острый пик на частотной характеристике.

В схеме универсального фильтра с единичным усилением на рис. 8,9, а частота fcp интеграторов определяет частоту fcp фильтра, а сопротивления п R задают величину а (или .Q) для полосового фильтра. Как правило, в этой схеме == R2

и Ci = Сг. В схеме универсального фильтра с коэффициентом усиления, большим единицы (рис. 8.9,6), величина а задается

Частота

Рис. 8.11. Принцип действия полосового фильтра на базе универсального активного фильтра.

ВЧ - частотная характеристика фильтра верхних частот, НЧ - характеристика фильтра нижних частот, ПФ - характеристика полосового фильтра.

сопротивлениями Ra и Rb инвертирующего усилителя. Выходное напряжение инвертирующего усилителя здесь суммируется непосредственно с Ubx и с выходным сигналом фильтра нижних

Р р

нчо-1-1-

вых

ЛУЗ

Рис. 8.12. Суммирующий усилитель для превращения универсального фильтра в фильтр-пробку. НЧ и ВЧ - выходы фильтров нижних и верхних частот соответственно в схеме универсального фильтра.

частот. Коэффициент усиления в полосе пропускания устанав- ливается с помощью сопротивлений Ri и Ro. с-

Универсальный активный фильтр легко превратить в фильтр-пробку, для чего нужно просто просуммировать имеющие противоположную фазу выходные сигналы фильтров верхних и нижних частот. Эти сигналы взаимно уничтожатся только на тех частотах, где перекрываются характеристики фильтров про-

пускания верхних и нижних частот. Если фильтр настроен как полосовой фильтр, то характеристика фильтра-пробки будет противоположна, т. е. вместо полосы пропускания у нее будет полоса подавления, и ей будет очень легко управлять. На рис. 8.12 показан сумматор, добавление которого к схеме универсального фильтра превращает последний в фильтр-пробку.

8.4.4. БИКВАДРАТНЫЙ ФИЛЬТР

Биквадратный (биквадный) фильтр - это очень стабильный активный фильтр, позволяющий (в случае полосового фильтра) получать значения Q, превыщающие 100. Биквадратные фильтры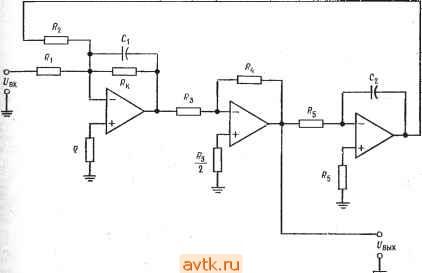

Рис. 8.13. Биквадратный полосовой фильтр.

если i= j, то f/g

= QU; если R=(QIK ) R,. то

легко соединять последовательно для получения многокаскадных фильтров. Одним из свойств биквадратного фильтра является неизменность его полосы пропускания при изменении (средней) частоты, так что в настраиваемых биквадратных фильтрах добротность увеличивается с ростом частоты. Схема биквадратного полосового фильтра показана на рис. 8.13. Она состоит из суммирующего интегратора, возбуждающего инвертирующий усилитель, который в свою очередь работает на

8.5. ПРОЦЕДУРЫ РАСЧЕТА КОМПОНЕНТОВ И ПРИМЕРЫ

В этом разделе рассмотрен расчет величин компонентов каждой из описанных в разд. 8.4 схем активных фильтров второго порядка. Все процедуры расчета будут сопровЬждаться примерами.

8.5.1. ФИЛЬТР НИЖНИХ ЧАСТОТ САЛЛЕНА И КЕЯ С РАВНЫМИ КОМПОНЕНТАМИ

В фильтре с равными компонентами Ri = R2 и Ci = С2. Начнем с выбора типа фильтра и величины fcp. Для этого:

1. Найдем из табл. 8.1 отношения /здб ср соответствующие выбранному типу фильтра. Если отношение/3g/fp =7 1, найдем ср: /ср = /здБ/(отнощение).

2. Выберем величину С и найдем R из соотношения

U=\l2nRC, (8.4)

где R = Ri = R2, С = Ci = С2. Возможно, этот шаг придется несколько раз повторить, чтобы найти разумное значение R.

3. Найдем из табл. 8.1 величину коэффициента затухания, соответствующую выбранному типу фильтра.

4. Выберем подходящее значение Ra- Часто оказывается удобным положить Ra = R. Найдем Rb КЗ соотношения

RB = {2-a)RA. (8.5)

второй интегратор. Если Ri = Rz, то коэффициент усиления схемы в полосе пропускания равен Rk/Ri. Среднюю частоту можно настраивать с помощью сопротивления 2. Сопротивление Rk задает добротность схемы.

Биквадратный фильтр действует следующим образом. Суммирующий интегратор вычитает из входного напряжения выходной сигнал фильтра нижних частот (они сдвинуты по фазе на 180°); на частотах, лежащих ниже переходного участка, эти сигналы взаимно уничтожаются, и выходной сигнал отсутствует. Когда частота достигает переходного участка, уменьшающийся выходной сигнал интегратора больше не может компенсировать входной сигнал, поэтому на выходе биквадратного фильтра появляется ненулевой сигнал. На частотах выше fo суммарный спад частотной характеристики двух последовательно соединенных интеграторов обеспечивает ослабление выходного сигнала, и таким образом формируется частотная характеристика полосового фильтра.

Таблица 8.1. Коэффициенты затухания и отношения /ffp для фильтров второго порядка

Для фильтра нижних частот fp=f3 д£(отио-шеиие). Для фильтра верхних частот f(.p = f3 дБ (о' ношение), где д5-желаемая частота среза на уровне 3 дБ; fp-частота, используемая при вычислениях; oTHomeHHe = f3 д£/(.р данной таблицы.

5. Найдем коэффициент усиления в полосе пропускания по формуле

Пример 8.1. Рассчитать компоненты фильтра нижних частот Саллена и Кея второго порядка. Фильтр должен иметь характеристику Баттерворта с fa дв = = 2 кГц.

Решение: из табл. 8.1 находим ?здб ср = Ь поэтому fa дб == f(,p- Выберем С = 0,1 мкФ = Ci = Cj. Положим Rl = R2 = R, Из соотношения fcp = = \/2tiRC имеем R = l/2nfcpC == 1/2л(2 кГц) (0,1 мкФ) = 796 Ом. Это значение R несколько меньше значения, желательного при использовании операционного усилителя 741, поэтому выберем С = 0,047 мкФ и еще раз найдем Я:

R = l/2nfcpC = 1/2л (2 кГц) (0,047 мкФ) = 1,69 кОм.

Используем номинал 1,69 кОм±2%. Положим Рд равным 10 кОм и найг Дем Rb:

Rb = (2 - ) == О (2 - 1.414) = 5,86 кОм. Используем номинал 5,9 кОм ± 2 %.

Коэффициент усиления определяется выбранным типом фильтра: К = Rb/Ra + 1 = (5.9 кОм/10 кОм) 4- 1 = 1,59.

Соберите показанную на рис. 8.14, а схему фильтра, использовав в ней полученные значения компонентов. Эта схема будет действовать как фильтр нижних частот Баттерворта второго порядка.

Замечание. Еще раз напомним, что из-за разброса параметров компонентов для точной установки желаемых значений fcp и а Может оказаться необходимой подстройка Ri, R2 и Rb-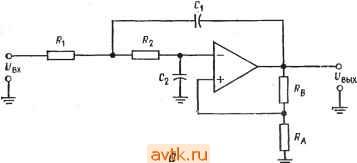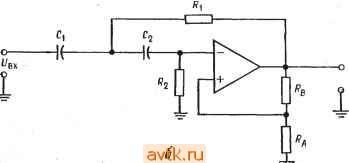

VsbK

Рис. 8.14. Активные фильтры Саллена и Кея. а-фильтр нижних частот второго порядка Саллена и Кея с равными компонентами: ,= 2, С, = С2, Кп=Дв/ + 1, fpp=l/2n C; б-фильтр верхних частот Саллена и Кея второго порядка с равными компонентами:

8.5.2. ФИЛЬТР ВЕРХНИХ ЧАСТОТ САЛЛЕНА И КЕЯ С РАВНЫМИ КОМПОНЕНТАМИ

Для нахождения компонентов схемы на рис. 8.14,6 нужно:

1. Выбрать тип фильтра и величину /3. Для выбранного типа фильтра найти по табл. 8.1 величину отношения /здеДср- Если это отношение не равно единице, найти fcp по формуле')

/ср = /з дБ (отношение). (8.6)

2. Положив С = Ci = Сг и R = Ri=R2, выбрать величину С и найти R из соотношения /ср= l/2nRC.

) Для фильтра верхних частот в табл. 8.1 приведено обратное отношение.-Лрнж ред.

*) Где Q определяется по /1 н /j в следующем пункте. - Прим. перев.

3. Из табл. 8.1 найти величину а, соответствующую выбранному типу фильтра. Выбрать Ra и найти Re по формуле Rb = = {2-a)RA. .

4. По формуле Кп = Яб/Яа + i найти коэффициент усиления в полосе пропускания.

Замечание. Оба фильтра (верхних и нижних частот) Саллена и Кея настраиваются следующим образом:

1. Величина fcp устанавливается совместным изменением Ci и Сг или и /?2.

2. Величина а устанавливается изменением Rb.

Пример 8.2. Рассчитать компоненты фильтра верхних частот Саллена и Кея второго порядка. Фильтр должен иметь характеристику Чебышева с неравномерностью 1 дБ и частотой среза fs дБ = 3 кГц

Решение: из табл. 8.1 находим /здб ср= 1>218, а= 1,059, fcp = /3flB 2) = 3 кГц (1,218) = 3,654 кГц.

Положим С = С] = Cj и R = R] = R2. Если выбрать С равным 0,022 мкФ, 70 R= l/2nfcpC= 1/2л(3,654 кГц) (0,022 мкФ) = 1,979 кОм. Используем номинал 1,96 кОм±2 %.

Положим /?л = 10 кОм, тогда = (2 - а)Л/1 = (2 - 1,059) 10 кОм = = 9,4! кОм. Используем номинал 9,53 кОм =fc 2 %.

К„ = Rb/Ra + 1 = (9.53 кОм/10 кОм) + 1, К„= 1,953.

8.5.3. ПОЛОСОВОЙ ФИЛЬТР

С ПАРАЛЛЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ

Показанная на рис. 8.15 схема с парал,лельной обратной связью может содержать или не содержать сопротив,ление R2. Ниже приводятся процедуры вычисления параметров компонентов схем с сопротивлением R2 и без него. Сопротивление Rz позволяет устанавливать желаемую величину коэффициента усиления в полосе пропускания. Процедура расчета для схемы без Rj

1. Выбрать fl и f2 и операционный усилитель, имеющий на этих частотах Л > 2Q2)

2. Для выбранных fi и найти fo и Q по формулам fo = -y/fif2 и Q - fo/{f2 - fl). Если окажется, что Q> 15, то следует ис-по,льзовать схему универсального фильтра или биквадратный фильтр. Если же Q < 15, то можно действовать дальше.

3. Выбрать С\ = €2 = С и найти

Ri = ll4nf,QC, Rs=l/2nkC. (8.7), (8.8)

4. Рассчитать Кп по формуле.

/Cn = 2q2. (8.9)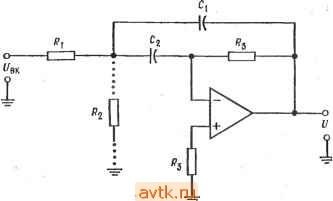

вых

Рис. 8.15. Полосовой фильтр с параллельной обратной связью.

Процедура расчета для схемы с R2

1. Выбрать /, и /г- Операционный усилитель должен на этих частотах иметь А > 2Q, где Q определяется по выбранным значениям f\ к f2 в следующем пункте.

2. Рассчитать /о и Q по формулам fo= лДТг и Q - fJifz - fi)-

3. Если полученное значение Q < 1 5, выбрать желаемое значение Кп коэффициента усиления в полосе пропускания; выбор Кп ограничен условием К„ < 2Q2.

4. Выбрать Ci = С2 = С и вычислить

R2 = Q/2nf{2Ct-K ). Rs = 2Q/2nf.

5. Проверить величину Кп по формуле

Krx-Rsfm-

(8.10) (8.11) (8.12)

(8.13)

Настройка схемы с параллельной обратной связью производится следующим образом: 1) fo устанавливается с помощью одновременного изменения Су и Сг или Ri и R2; 2) Q устанавливается с помощью изменения величины отношения Rs/Ri, причем произведение R3R1 должно оставаться постоянным; 3) коэффициент уси,ления в полосе пропускания устанавливается с помощью изменения R2.

Пример 8.3 Рассчитать компоненты схемы с параллельной обратной связью без Ri, реализующей полосовой фильтр. Отсутствие R2 обеспечивает максимальное значение коэффициента усиления в полосе пропускания. Фильтр должен иметь fi == 4,5 кГц и /2 = 5,5 кГц. . . .

2л/оС 2я (822,4 Гц) (0,0047 мкФ)

= 521 кОм.

Используем номинал 511 кОм ±2%.

Проверим с помощью выражения (8.13) величину Кп.

К„ = Rs/2Ri = 511 кОй/2 (26,1 кОм) = 9,79.

Если нас устраивает полученное значение iCn = 9,79 вместо желаемого Кп = 10, то расчет можно считать законченным. В противном случае cлeдyet немного увеличить Rs и немного уменьшить

8.5.4. УНИВЕРСАЛЬНЫЕ ФИЛЬТРЫ

Ниже приведена процедура расчета компонентов схемы универсального фильтра с единичным усилением, показанной на рис. 8.16.

Процедура расчета для универсальных фильтров с единичным усилением. Фильтры верхних и нижних частот

1. Выбрать величину f и тип фильтра.

2-. По табл. 8.1.найти отношение/gg/f. Если Upjhv

числить /ср.

3. Положить /?, = /?2 = 7?з = /?4 = = = Выбрать С =. = С, = С2 и найти R = 1/2я/срС.

- Найти по табл. 8.1 значение а, соответствующее выбранному типу фильтра и найти /?5 по формуле

п,Клт-я (8.14)

Решение: /о = У/Тг = V{4.5 кГц) (5,5 кГц) = 4,975 кГц, Q =/ /(/ - f,) = 4,975. Выберем. С = d = С2 = 0,001 мкФ. Из формулы (8.7) находим R, = 1/4л/оС2С= 1/4л(4,975 кГц) (4,975) (0,001 мкФ) =3,215 кОм. Используем номинал 3,32 кОм ±2 %.

Из формулы (8.8) находим Лз = 2(Э/2л/оС = 2(4,975)/2л(4,975 кГц) X X (0,001 мкФ = 318 кОм. Используем номинал 316 кОм ±2 %.

Из формулы (8.9) находим ТСп = 2Q2 = 2 (4,975) = 49,5. На частоте 5 кГц практически любой операционный усилитель имеет А > 50, так что выбор пригодного для данной задачи усилителя не вызывает затруднений.

Пример 8.4. Рассчитать компоненты полосового фильтра с параллельной обратной связью, имеющего fi = 760 Гц, /а = 890 Гц а Кп = 10. Поскольку величина Кл задается, надо использозать схему с R2.

Решение. /о = V/./2 = V(760 Гц) (890 Гц) = 822,4 Гц, Q = (f - f,) =. = 822,4 Гц/(890 Гц - 760 Гц) i= 6,326. Выберем Ci = Cs = С = 0,0047 мкФ.

По формулам (8.10) - (Й.12) рассчитаем Ri, R2 и R:

Rl = Q/2nfcCKn = 6,326/2я (822,4 Гц) (0,0047 мкФ) 10 = 26 кОм. Используем номинал 26,1 кОм ±2 %.

С? I g 326

= 2л/оС (2Q2 г= 2я (822,4 Гц) (0,0047 мкФ) 10

Используем номинал 3,83 кОм ±2 %.

о 20 2(6,326)

Настройка схемы:

1) Настройте fcp с помощью одновременного изменения Ri и R2 или С, и Сг.

2) Настройте а с помощью изменения Ro. с-

Процедура расчета для универсальных фильтров с единичым усилением. Полосовой фильтр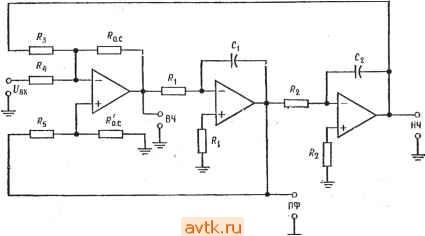

Рис. 8.16. Схема универсального активного фильтра второго порядка с единичным коэффициентом усиления. ВЧ, НЧ и ПФ - выходы соответственно фильтров верхних частот, нижних частот и

полосового.

1. Выбрать fi и f2. Для универсального фильтра с единичным усилением Кп = Q.

2. Найти fo и Q. Величина Q может достигать значения 100.

3. Выбрать C = Ci = C2 и рассчитать R = Ry = R=: R = R==

= o. с = o. с ПО формуле R = l/2nfoC.

4. Найти Rs no формуле

R5-K.AQ-)- (8-15)

Настройка фильтра:

1) Настройте fo с помощью одновременного изменения Ri и R2 или Ci и Сг.

2) Настройте Q с помощью изменения R .

Пример 8.5. Рассчитать компоненты схемы универсального фильтра с единичным усилением, реализующей фильтр нижних частот Чебышева. Порядок фильтра равен двум, fgд5=12кГц, неравномерность характеристики 2 дБ.

Значение коэффициента усиления в полосе пропускания фиксировано и равно единице.