

 |
 |
|
Разделы
Публикации
Популярные
Новые
|
Главная » Применение операционных усилителей 1 ... 16 17 18 19 20 21 22 ... 57 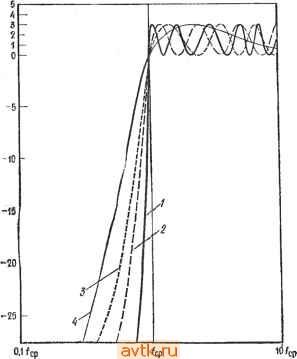 Рис. 8.36. Частотные характеристики фильтров Чебышева. Верхних частот с неравномерностью в полосе пропускания 3 дБ - шестого порядка (/), четвертого порядка (2), третьего порядка (3), второго порядка (4); f частота среза. И ЧТО его величина меняется в зависимости от неравномерности характеристики в полосе пропускания, как и на рис. 8.3а. Пиковая частота f связана с частотой среза fcp соотношениями fn = fcpV2 - ( /2) (для фильтра нижних частот). JJ fп = /ср/V1 - ( /2) (для фильтра верхних частот), где а -коэффициент затухания. Ниже в этой главе коэффициент затухания будет рассмотрен бблее подробно. 18.3.3. ФИЛЬТР БЕССЕЛЯ t О фильтрах Бесселя говорят как о фильтрах с линейной фазой или с линейной задержкой. Это значит, что запаздывание По фазе сигнала на выходе фильтра относительно сигнала на его входе линейно возрастает с частотой. Поэтоглу фильтры Бесселя почти не дают выброса при подаче на их вход ступенчатых сигналов. Это свойство делает такие фильтры наиболее подходящими для фильтрации прямоугольных колебаний без изменения их формы. Фильтры Бесселя имеют наклон характеристики на переходном участке менее 6 дБ/октава. Частота среза фи.пьтра Бесселя определяется как частота, на которой запаздывание по фазе равно половине запаздывания, максимально возможного для данного фильтра: е (/ср) = е„акс/2 = (пя/2)/2 рад, где 6 -запаздывание по фазе, п -порядок фильтра. При таком определении частота среза фильтра Бесселя ке равна его частоте на уровне 3 дБ. Это можно видеть из рис. 8.4, 0.01 ь J-1 I 1.1 I 11 1 I I 11111 I I 1 I.J 10/, Рис. 8.4. Частотные характеристики фильтра нижних частот Бесселя второго порядка. Наклон на переходном участке менее 6 дБ/октава на один полюс. Q = Ш2-h) = /hf2/{f2-f), (8.2) где fo=V/i/2-средняя частота, fi -нижняя частота среза на уровне 3 дБ, /г - верхняя частота среза на уровне 3 дБ. Для активных фильтров Q= 1/а. Коэффициент усиления в полосе пропускания Кп активного фильтра равен отношению выходного напряжения к входному: иа KOTCJpoM приведена амплитудно-частотная характеристика фильтра Бесселя. 8.3.4. ДРУГИЕ типы ЧАСТОТНЫХ ХАРАКТЕРИСТИК Из сех известных типов фильтров в этой главе рассматриваются лишь фильтры Бесселя, Баттерворта и Чебышева. Существуют и другие типы фильтров, в частности обратный фильтр Чебышева, характеристика которого равномерна в полосе пропускания, но имеет зубцы в полосе подавления; эллиптический фильтр с характеристикой, имеющей очень крутой наклон на переходном участке, но неравномерной и в полосе пропускания, и в полосе подавления; параболический фильтр, обладающий очень хорошей импульсной характеристикой. Более подробные сведения об этих фильтрах читатель может найти в книгах, перечисленных в конце главы. 8.3.5. НЕКОТОРЫЕ ОПРЕДЕЛЕНИЯ Коэффициент затухания а определяет форму характеристики на переходном участке и вид выброса характеристики в полосе пропускания вблизи переходного участка. Таким образом, коэффициент затухания определяет форму частотной характеристики фильтра, т. е. его тип. Так, фильтр Баттерворта второго порядка имеет коэффициент затухания а, равный 1,414, а фильтр Чебышева второго порядка с неравномерностью 3 дБ имеет а = = 0,766. Одна и та же схема в зависимости от выбора значений ее компонентов может действовать как фильтр Бесселя, фильтр Баттерворта или фильтр Чебышева, и форма частотной характеристики фильтра определяется коэффициентом затухания. На рис. 8.5 показано несколько характеристик фильтров нижних частот при различных значениях коэффициента затухания. Добротность Q связывает среднюю частоту полосы пропускания и ее ширину на уровне 3 дБ; рис. 8.6 иллюстрирует эту связь. Численно добротность равна 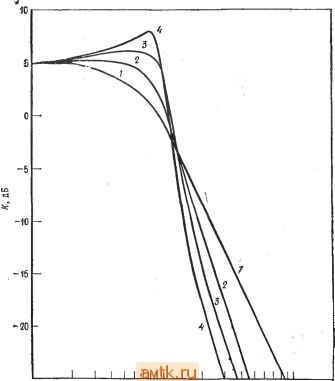 Частота Рис. 8.5. Частотные характеристики фильтров нижних частот при различных значениях коэффициента затухания. / - а = 1,732, фильтр Бесселя; 2 -а =1,414, фильтр Баттерворта; 3 - фильтр Чебышева с неравномерностью 1 дБ; 4 - фильтр Чебышева с неравномерностью 3 дБ. Чувствительностью S одного из параметров фильтра по отношению к другому его параметру называется отношение величины изменения первого параметра к величине изменения второго, если изменение второго параметра вызвало изменение первого. Например, равенство SZ = -0,5, где соо = 2nfo, а Ri - сопротивление резистора в схеме активного фильтра, показывает, что соо уменьшается на 0,5%, если Ri увеличивается на 1 %. Часто приходится рассчитывать чувствительность таких параметров полосовых фильтров, как fcp, о, а и Q. Соответствующие вычисления утомительны и требуют больших затрат вре- 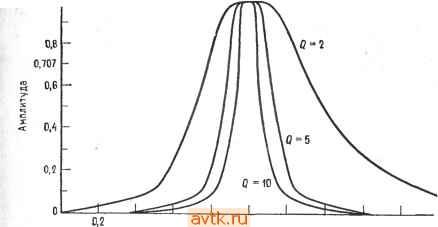 0, 0,6 1.6 1,8 Частота Рис. 8.6. Частотные характеристики полосовых фильтров. - мени, но их приходится выполнять, если предполагается использовать фильтр в широком диапазоне внешних температур или если параметры компонентов фильтра имеют большой разброс. Выражения для 5 имеют разный вид для различных типов If фильтров; они приведены в некоторых книгах, указанных в конце главы. Нам в этой главе такие выражения не встретятся. 8.3.6. КОМПОНЕНТЫ СХЕМ ФИЛЬТРОВ Для обеспечения высокого качества работы активных фильтров в их схемах следует использовать компоненты, параметры которых имеют малый разброс. Сопротивления и конденеаторы должны иметь малые температурные коэффициенты и малый временной дрейф параметров. Для схем фильтров второго порядка можно рекомендовать конденсаторы с допуском ±5 % и сопротивления с допуском ±2%. Для фильтров более высоких порядков лучше взять сопротивления с допуском ±1 % и конденеаторы с допуском ±2 7о- Однако использование компонентов даже с таким небольшим разбросом параметров не гарантирует от необходимости некоторой дополнительной подстройки, которая может понадобиться для получения желаемых величин коэффициента затухания и частоты активного фильтра. В схемах активных фильтров лучше всего использовать металлопленочные сопротивления, так как оии имеют низкий уровень собственных шумов, очень хорошую частотную характеристику и весьма низкие температурные коэффициенты сопротивления (ТКС). Так, в продаже имеются металлопленочиые сопротивления с температурными коэффициентами ±100-10-6 1/°С и ±50-10-6 1/°С,. но существуют и могут'быть заказаны и сопротивления с ТКС = ±10-10- 1/°С. В низкочастотных фильтрах очень хороши проволочные сопротивления, так как они имеют низкий уровень шумов,; малый температурный дрейф (ТКС около. ±10-10- 1/°С), высокую точность и выпускаются в широком ассортименте номиналов. Заметим, что даже для работы на умеренных частотах следует использовать проволочные сопротивления с безындукционной намоткой.- Углеродистые тонкопленочные сопротивления также выпу- скаются в широком ассортименте номиналов и обладают высокой точностью, очень низким уровнем шумов, хорошей частотной характеристикой и прекрасными температурными коэффициентами. Однако ввиду их высокого уровня шумов и плохой температурной стабильности углеродистые объемные сопротивления мало подходят для использования в схемах активных фильтров, поэтому следует избегать их применения иначе как в чисто экспериментальных целях. Из конденсаторов в активных фильтрах лучше всего исполь зовать полистироловые, высококачественные керамические и слюдяные. Все они при данной емкости относительно дороги и велики по габаритам, но зато обладают малыми тангенсами углов диэлектрических потерь и низкими температурными коэффициентами. Слюдяные конденсаторы существуют только до величин порядка 0,01 мкФ, а полистироловые - приблизительно до 10 мкФ. В случаях когда требования к качеству работы фильтра невелики, например при проведении лабораторных работ в школах, можно использовать конденсаторы на металлизированном майларе или поликарбонатные. Использования в активных фильтрах небольших по размеру дисковых керамичег ских конденсаторов следует избегать, так как в зависимости от напряжения, температуры, времени и частоты их емкость может меняться на величину до нескольких процентов. При проведении лабораторной работы к этой главе можно пользоваться металлопленочными или углеродистыми тонкопленочными сопротивлениями и майларовыми конденсаторами, так как температурная стабильность в данном случае роли ие играет. 8.4. НЕКОТОРЫЕ ТИПЫ АКТИВНЫХ ФИЛЬТРОВ В этом разделе будут рассмотрены некоторые схемы активных фильтров, а в следующем - расчет их компонентов. 8.4.1. ФИЛЬТР САЛЛЕНА И КЕЯ (УНИН) УНИН -это управляемый напряжением источник напряжения. В схемах Саллена и Кея операционный усилитель используется как УНИН. Схемы активных фильтров пропускания, нижних и верхних частот Саллена и Кея второго порядка показаны  т  -о Рис. 8.7. Активные фильтры Саллена и Кея. а - фильтр нижних частот второго порядка, Rt = Дг, Ci - Са; б - фильтр верхних частот второго порядка. на рис. 8.7. Эти схемы популярны и недороги, и их легко настраивать. Б обеих схемах каждая из /?С-цепей вносит 6 дБ/октава в наклон характеристики на переходном участке. Эти Схемы содержат по две /?С-цепи (RiCi и R2C2), поэтому соотг ветствующие фильтры имеют второй порядок. В фильтре пропускания нижних частот цепи RiCi и R2C2 являются интегрирующими, а в фильтре пропускания верхних частот - дифференг Пирующими. Сопротивления Ra и Rb определяют крэффициент затухания. Характеристика вблизи края полосы пропуска-ния формируется за счет обратной связи, которая осуществляется через конденсатор Ci в случае фильтра пропускания нижних частот или через сопротивление Ri в случае фильтра пропускания верхних частот. Если Ri = R2 и Ci = Сг, то величины компонент таких фильтров легко рассчитать. Коэффициент усиления фильтров Саллена и Кея должен оставаться постоянным при изменениях Ra и Rb, необходимых для установки коэффициента затухания и вместе с ним типа фильтра. i 8.4.2. ФИЛЬТР С ПАРАЛЛЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ Фильтр с параллельной обратной связью -это простой полосовой фильтр, хорощо работающий при низких и умеренных 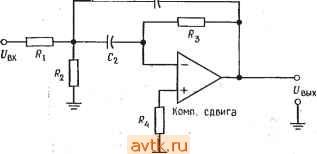 . Рис. 8.8. Полосовой фильтр с параллельной обратной связью. (приблизительно до 10) значениях добротности; его схема показана на рис. 8.8. Обратите внимание на то, что обратная связь в этой схеме осуществляется одновременно через включенные параллельно Rs и Ci (отсюда и название схемы). Часть характеристики, соответствующая фильтру пропускания нижних частот, формируется с помощью цепи Ri и. Ci, а часть, соответствующая фильтру пропускания верхних частот, - с помощью цепи Rz и Сг- Такая обратная связь обеспечивает положение максимума характеристики вблизи частоты fo- Сопротивление R2 можно убрать, но в этом случае изменится процедура вычисления величин компонентов схемы. Сопротивление R2 служит для увеличения Rbk и обеспечивает возможность задавать коэффициент усиления в полосе пропускания. Величины компонентов этой схемы в обоих ее вариантах (с сопротивлением R2 и без .него) -будут рассчитаны в следующем разделе. Фильтры с параллельной обратной связью могут быть сконструированы и как фильтры пропускания верхних или нижних частот. 8.4.3. УНИВЕРСАЛЬНЫЙ (МНОГОЦЕЛЕВОЙ) ФИЛЬТР Показанная на рис. 8.9, а схема универсального активного фильтра называется универсальной с единичным усилением, потому что ее коэффициент усиления в полосе пропускания равен единице. Эта схема может действовать одновременно как фильтр верхних частот, фильтр нижних частот и полосовой фильтр (все - второго порядка). При этом частотная характеристика полосового фильтра зависит от характеристик фильтров верхних и нижних частот. Если, например, эти два фильтра имеют частотные характеристики типа Баттерворта, то порядок полосового фильтра будет равен единице. Поскольку все три характеристики (полосового фильтра и фильтров верхних и нижних частот) формируются при помощи одних и тех же компонентов, характеристики фильтров верхних и нижних частот должны быть одного типа, т. е. оба типа Баттерворта или оба типа Чебышева с неравномерностью 3 дБ. Заметим, что характеристику полосового фильтра нельзя оптимизировать одновременно с характеристиками фильтров верхних и нижних частот. Универсальный фильтр имеет высокую стабильность и низкую чувствительность Q и а, а настройка частоты и настройка добротности такого фильтра мало влияют друг на .друга. В качестве полосового фильтра универсальный фильтр может иметь устойчивую добротность, достигающую 100. Схема универсального активного фильтра используется во многих серийно выпускаемых активных фильтрах. Универсальный фильтр относительно сложен, так как содержит три операционных усилителя в варианте с единичным коэффициентом усиления и четыре операционных усилителя в варианте с независимой настройкой коэффициента усиления и а. Этот последний вариант схемы универсального фильтра показан на рис. 8.9, б. Принцип действия универсального фильтра можно объяснить двумя способами. Первый из них иллюстрируется рис. 8.10. Схему универсального фильтра можно рассматривать как построенную на интеграторах схему решения дифференциального уравнения второго порядка, в основном аналогичную схему из примера 6.17 в гл. 6. Основной вариант схемы активного фильтра состоит из сумматора и двух интеграторов. Интеграторы обеспечивают формирование частотной характеристики, и их выходные напряжения подаются обратно на сумматор, причем коэффициент усиления 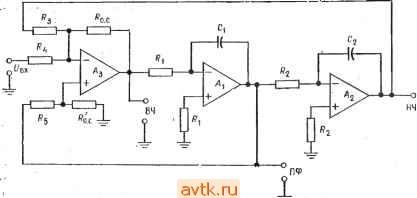 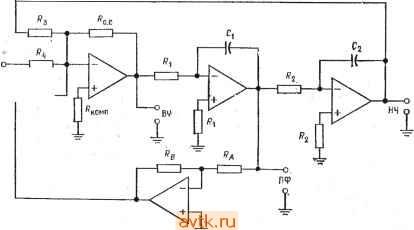 Рис. 8.9. Универсальные активные фильтры. а - фильтр второго порядка с единичным коэффициентом усиления: б - фильтр с из меняемым коэффициентом усиления. ВЧ - выход фильтра верхних частот, НЧ - выход фильтра нижних частот, ПФ - выход полосового фильтра. В петле обратной связи определяет а. Чтобы лучше понять, как работает этот фильтр, рассмотрим каждую из характеристик отдельно. Два соединенных последовательно интегратора обеспечивают формирование характеристики фильтра нижних частот второго порядка. Подавая выходное напряжение первого интегратора с настраиваемым коэффициентом передачи в цепи .обратной 1 ... 16 17 18 19 20 21 22 ... 57 |
|
© 2004-2026 AVTK.RU. Поддержка сайта: +7 495 7950139 в тональном режиме 271761
Копирование материалов разрешено при условии активной ссылки. |