Если используемый в дифференциаторе операционный усилитель имеет скорость нарастания, слишком низкую для того, чтобы он успевал реагировать на изменение входного сигнала с той же скоростью, с какой этот сигнал меняется, то прн очень малой длительности входного сигнала напряжение на выходе дифференциатора может и не достигать максимально возможного значения. Если, например, наша прямоугольная волна имела бы время нарастания 1 НС, то скорее всего не было бы вообще никакого изменения выход-ного напряжения).

Рпример 6.11. Какие значения Лк и Ск следовало бы использовать в примере 6.9, где R = \0 кОм н С = 0,1 мкФ, если максимальный коэффициент усиления равен 1000 и максимальная частота дифференцируемого сигнала равна 10 кГц при допустимой ошибке 1 7о?

Решение: По табл. 6.1 находим, что при погрешности 1 % максимальная рабочая частота должна быть равна макс = (0,1) 1/(2яЛкС). Так как нас интересует только дифференцирование, полагаем \l2nRJ2 = 1/2яЛСк = = 10(10 кГц) = 100 кГц. Максимально допустимый коэффициент усиления приблизительно равен RIRk, поэтому Rk = Л/1000 = 10 Ом; Ск определяется-из соотношения ЛкС = ЛСк, так что С = ЛкС/R = (10 Ом) (0,1 мкФ)/ /10 кОм == 0,001 мкФ.

6.14. СУММИРУЮЩИЙ ДИФФЕРЕНЦИАТОР

Подобно другим решающим схемам, которые рассматривались выше, дифференциатор может иметь более одного входа..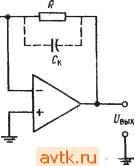

Рис. 6.21. Суммирующий дифференциатор.

Обращаясь к рис. 6.21, можно видеть, что -==с^ +с^ +

п' сли п - число входов дифференциатора. Так как: Цых = inR и ic == CdUc/dt, выходное напряжение можно пред-

) Это так, если дифференциатор почти идеален. Но любой короткий Фронт вызовет экспоненциальный процесс в суммирующей точке, а степень перегрузки н длительность этого процесса будут зависеть от величины С и параметров входной цепи ОУ. - Прим. ред.

ставить в виде

dUl , rff/2

2 dt

Естественно, в этой схеме следует ввести динамическую стабилизацию.

6.15. ДИФФЕРЕНЦИАТОР-УСИЛИТЕЛЬ

Дифференциатор-усилитель сочетает в одной решающей схеме способность реагировать как на величину, так и на скорость изменения входного сигнала. Эта схема, по существу, представляет собой комбинацию усилителя и дифференциатора. Как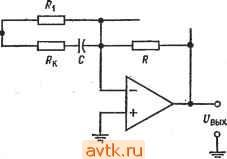

Рис. 6.22. Дифференциатор-усилитель. f/вых-( / i)t/i- C(dt/,/dt).

И дифференциатор, она может иметь более одного входа. Выходной сигнал дифференциатора-усилителя имеет вид

RnuK==-iRlRi)Ui-RC-. (6.18)

Схема дифференциатора-усилителя показана на рис. 6.22.

6.16. РАЗНОСТНЫЙ ДИФФЕРЕНЦИАТОР

Как и интегратор, дифференциатор можно использовать в варианте с дифференциальным входом. Соответствующая схема показана на рис. 6.23. Ее выходной сигнал имеет вид

f/вых = i?C[d(t/2-t/,)/]. (6.19)

Для минимизации ошибки следует при конструировании такой схемы позаботиться о хорошем согласовании ее компонент.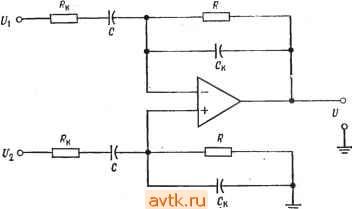

Рис. 6.23. Разностный дифференциатор.

вых

6.17. РЕШЕНИЕ

ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ

Одно из применений схем дифференциаторов и интеграторов заключается в их использовании для решения уравнений, в ко-эрые входят скорости изменения переменных величин'). Пусть например, надо найти ток в (CL-цепи на рис. 6.24. Чтобы сделать, выразим состояние кемы через производные пере-1енной по времени.

Применим закон Кирхгофа сумме падений напряжения данной цепи:

Ubx = Ui + Uc + Ui,. (6.20)

i=0,5 Гн

= 10 Ом

: С=0,5мкФ

Рис. 6.24. Л/-С-цепь.

1адение напряжения на сопротивлении равно просто iR, что можно записать

UndQldt. (6.21)

Мгновенное значение падения напряжения на индуктивности имеет вид

Ul = ~L (di/dt) = - I (dQ/df). (6.22)

Согласно определению емкости, С = Q/Uc, и падение напряжения на конденсаторе равно

Uc = Q/C. (6.23)

) Обыкновенных дифференциальных уравнений. - Прим. ред.

Подставим выражения (6.21) -(6.23) в равенство (6.20) и подучим уравнение -

t/e, = - L {dPQIdf) -f R (dQ/dt) + (Q/C).

Правая часть этого уравнения содержит производные убывающего порядка от одной и той же переменной величины. Это уравнение можно преобразовать таким образом, чтобы получилось уравнение относительно Q:

Q = LC (dQ/df) - RC (dQ/dt) + CU. (6.24)

Теперь построим сумматор для нахождения Q и подадим на каждый из его входов одно из слагаемых правой части уравнения (6.24). Прежде всего подставим в уравнение (6.24) величины элементов схемы рис. 6.24 и получим

Q = (0,5 Гн) (0,5 мкФ) (OQ/dt) - 10 Ом (0,5 мкФ) (dQ/dt) +

+ 0,5 шкФих = [0,25 (dQ/dt) - 5 (dQ/dt) + 0,5C/,J (10-) Кл.

Для упрощения масштаба будем формировать ответ в микрокулонах (мкКл). Этот ответ продифференцируем и полученные значения тока в микроамперах подадим на один из входов сумматора. В нашей решающей схеме используем отдельные инвертирующие сумматоры, что даст возможность обойти проблему обеспечения баланса схемы сложения-вычитания. Напомним, что для получения на выходе инвертирующего сумматора сигнала определенного знака на его вход следует подавать сигнал противоположного знака; например, для получения С/вых = = -X -f У на входы надо подать +Х и -У.

Схема для решения дифференциального уравнения, описывающего цепь на рис. 6.24, показана на рис. 6.25. Как и при решении систем линейных алгебраических уравнений, масштабы в этой схеме должны быть выбраны таким образом, чтобы ответ мог уместиться в шкале напряжений ОУ. При помощи показанной на рис. 6.25 схемы можно исследовать зависимости тока от времени в цепи на рис. 6.24 для различных видов входного сигнала.

Уравнение, описывающее цепь на рис. 6.24, можно также записать и через интегралы от одной переменной величины и решить при помощи схемы на интеграторах. Такая схема будет, вообще говоря, более устойчивой, чем показанная на рис. 6.25 схема иа дифференциаторах. Решение через интегралы выглядит следующим образом:

Из выражений Uc - Q/C и ic - dQ/dt следует равенство dQ = = idt. Интегрируя, получим Q = /Л; теперь можно написать

VB.Vi, + U + U, = iR~L() + [)\idt.

0.5 МОм

х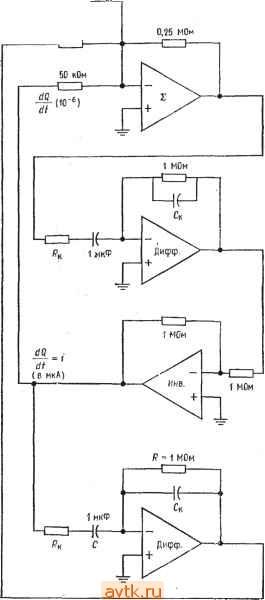

0 = 0.25-5.0.51/ ( в Л1ККЯ )

(в мкА)

(10-6)

Рис. 6.25. Схема решения дифференциального уравнения.

и^= -L [dQIdt) + R {dQldt) + {QIC).

500 kOm

100 kOm 100 kOh

100 kOm

50 kOm

100 kOm

100 kOm

100 kOm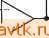

-20/irt

25 kOm

1 мкФ 60 иОм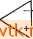

50 Ом

10 кОм 2 МОм

10 кОм

10 кОм

f/вых =

0,1 мкФ

10 кОм

Рис. 6.26. Схема решения уравнения.

0.5 Гн + (0,5 мкФИО.5 Гн) оАг \ х dt =

= 20idt + 4-l0idt-2 Jt/ex*.

Схема на интеграторах для решения этого уравнения показана на рис. 6.26. Отметим, что для реализации в схеме множителя 10 во втором члене правой части уравнения этот множитель ввиду его большой величины пришлось разбить на сомножители и реализовать их отдельно на усилителе с коэффициентом усиления 200 и интеграторе с коэффициентом усиления 1000.

Если напряжение Ubx переменное, то в интеграторах следует использовать корректирующие сопротивления р. Если t/вх - ступенчатая функция, то напряжение на конденсаторах интеграторов следует периодически сбрасывать, как это делается, например, в трехрежимном интеграторе. Если в интеграторах использованы операционные усилители со входом на полевых транзисторах, то максимальное время, по истечении которого сброс становится необходимым, увеличивается.

1. Напряжение на выходе интегратора пропорционально среднему по времени от его входного напряжения. Частотная характеристика интегратора должна иметь спад -6 дБ/октава в диапазоне частот, в котором схема используется как интегратор.

2. Выходное напряжение интегратора удовлетворяет уравнению

VBu.= -\lvdt. (6.2)

3 Если интегратор используется для интегрирования переменных напряжений, то для уменьшения его чувствительности к дрейфу напряжения сдвига и.к заряду конденсатора током смещения следует параллельно С включать Корректирующее сопротивление Rp. Для получения хорошей точности нижняя Граничная частота должна быть задана на уровне не более /ю наинизшей частоты интегрируемого сигнала; при наличии Лр эта граничная частота равна 1= lJ2nRpC.

Интегрируя по времени обе части этого равенства, получим

потому что интеграл от di/dt равен просто i. Решая это уравнение относительно /, найдем

Li = Ridt + \ idt-Udt,

i==i\idt + \\idt-L\udL

Подставляя сюда величины элементов цепи, получим 10 Ом г . . 1 f f - 1

при которых Свых = - 5С| - 10 Cl dt.

6.9. Указать назначение каждого из режимов трехрежимного интегратора.

6.10. Вычислить R, при котором двойной интегратор, включенный как генератор, будет самовозбуждаться на частоте 20 кГц, если С = 0,1 мкФ.

) Во всех случаях / выразить в секундах. - Прим. ред.

4. Если интегратор используется для интегрирования медленно меняющихся сигналов, то конденсатор интегратора следует периодически разряжать (сбрасывать), чтобы напряжение на нем, вызванное протеканием через конденсатор тока смещения, не могло привести к появлению чрезмерной ошибки.

5. Если R к Rp выбраны так, чтобы обеспечить желательный коэффициент усиления по напряжению, а С выбрана так, чтобы задать желательную первую граничную частоту, то интегратор можно использовать как /?С-фильтр низкой частоты с усилением.

6. Выходное напряжение дифференциатора пропорционально скорости изменения входного напряжения. Выражение для выходного напряжения дифференциатора имеет вид

Упык = -RC (dUxIdt). (6.13)

7. Коэффициент усиления дифференциатора должен расти с наклоном 6 дБ/октава в диапазоне частот, в котором схема используется как дифференциатор. Такая частотная характеристика обеспечивается применением конденсатора на входе.

8. Во избежание появления нежелательных высокочастотных шумов на выходе дифференциатора его следует корректировать. Для осуществления коррекции параллельно R включается конденсатор Ск. Для получения хорошей точности Ск надо выбирать таким образом, чтобы частота \l2KRCy. приблизительно в десять раз превышала наибольшую частоту дифференцируемого сиг-кала.

9. Так как дифференциатор имеет емкостной вход, следует во избежание перегрузки источника напряжения Свх включать последовательно с С сопротивление Rk. Это сопротивление выбирается так, чтобы выполнялось равенство 1/2я/? С = 1/2я/?Ск.

10. Дифференциатор можно использовать как полосовой фильтр пропускания, если отношение RIRk выбрать равным коэффициенту усиления в полосе пропускания, С выбрать так, чтобы нижняя частота фильтра на уровне 3 дБ была равна 1/2я/?кС, а Ск -так, чтобы 1/2я/?Ск было равно верхней частоте фильтра иа уровне 3 дБ.

КОНТРОЛЬНЫЕ ВОПРОСЫ

6.1. Объясните принцип действия интегрирующей схемы.

6.2. Для интегратора на рис. 6.2 найти R, при котором С/вых ~ ~ если С = I мкФ.

6.3. Вычислить Свых через 2 мс после подачи входного сигнала на интегратор (п. 6.2), если а) Ubx = 3<; б) Свх = 2/2; в) С/вх = 2е ).

6.4. Перечислить три причины, по которым время интегрирования в реальных схемах ограничено.

6.5. Для каждого из факторов, ограничивающих время интегрирования, указать способ компенсации.

6.6. В интеграторе R = 2Q кОм. Вычислить Rp и С, если интегратор должер использоваться как фильтр низких частот с коэффициентом' усиления 10 й fi = 10 кГц.

6.7. Назовите цели, с которыми применяются схемы ограничения.

6.8. В иитеграторе-усилителе на рис. 6.10 R= 100 кОм. Вычислить Ro.c и С,

6.11. Вычислить с, при котором выходное напряжение дифференциатора будет иметь вид {Увых = -0,00\dUBx/dt, если R = 100 кОм.

6.12. Если Ubx = 4t, то чему будет равно выходное напряжение дифференциатора из п. 6.11 через а) 2 мс; б) 40 с после подачи входного сигнала?

6.13. Скажите, зачем надо вводить стабилизирующую коррекцию в дифференциатор.

6.14. Для дифференциатора на рис. 6.16, имеющего С = 0,1 мкФ, вычислить Rk, R и Ск, при которых максимзльная частота дифференцируемого сигнала будет равна 20 кГц, а К = 1000.

6.15. Вычислить Rk, R и Ск так, чтобы дифференциатор на рис. 6.16 действовал как полосовой фильтр с полосой пропускания от 500 Гц до 2 кГц и с коэффициентом усиления в полосе пропускания, равным 20. Положите С = = 0,1 мкФ.

6.16. На частоте 1 кГц задана точность дифференциатора I %. Найти наи-меньшее допустимое значение верхней границы (fi) полосы дифференцируемых частот.

Если вы не можете ответить на некоторые вопросы, отметьте их и еще раз просмотрите соответствующие разделы текста, чтобы найти ответы.

ЛАБОРАТОРНАЯ РАБОТА

Цели работы. После выполнения этой лабораторной работы учащийся должен уметь построить интегратор и дифференциатор для получения интеграла или производной от заданного сигнала. Используя интегратор и дифференциатор, студент должен будет проверить, что дифференцирование и ин-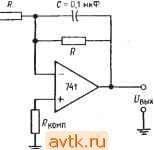

С= 0,1 мкФ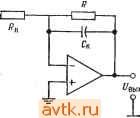

Рис. 6.27. Интегратор.

Рис. 6.28. Дифференциатор.

тегрпрование суть взаимно обратные операции. Кроме того, студент должен научиться включать двойной интегратор в режиме генератора. ( В качестве факультативного упражнения студент может решить дифференциальное уравнение при помощи сумматоров, инверторов и дифференциаторов (интеграторов).

Оборудование. 1. Два операционных усилителя рА741 фирмы Fairchild или их аналог и их заводской паспорт. 2. Набор сопротивлений точностью 2%. 3. Источник питания ±15 В пост. тока. 4. Набор майларовых конденсаторов. 5. Генератор сигналов, способный давать синусоидальные, прямоугольные и треугольные колебания. 6. Двухлучевой осциллограф. 7. Потенциометр на 10 кОм. 8. Макетная панель с гнездами для ИС, такая, как EL Instruments SK-10.

Порядок выполнения работы. 1. Интегратор, (а) Собрать по схеме на

рис. 6.27 интегратор, дающий выходной сигнал вида С^вых'

.2000

Uidt.

Скорректировать этот интегратор таким образом, чтобы нижняя частота интегрирования была равна приблизительно 30 Гц. Установить нуль сдвига, (б) Рассчитать и проверить экспериментально вид выходного сигнала для следующих входных сигналов: 1) синусоидальная волна частотой 1 кГц и амплитудой 2 В; 2) прямоугольная волна частотой 1 кГц и двойной амплитудой 5 В. (в) Подобрать R к С так, чтобы интегратор действовал как активный фильтр низких частот с коэффициентом усиления 5 и /i = 500 Гц. Проверьте

Частота

Рис. 6.29. Частотная характеристика полосового фильтра.

f, 320 Гц, fa 5 5 кГц.

работу этого фильтра, измерив коэффициент усиления на низких частотах и частоту среза fcp. При проверке используйте синусоидальный входной сигнал. 2. Дифференциатор, (а) Соберите схему, показанную на рис. 6.28, так, чтобы'

10 кОм

/? = 10 кОм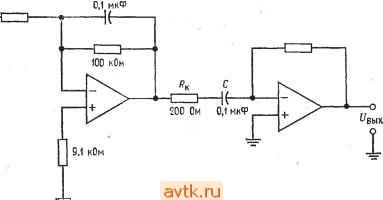

Рис. 6.30. Схема, демонстрирующая взаимную обратимость дифференцирова-

иня и интегрирования.

получить выходное напряжение вида fHx = -0,1 10-2({Ув>1/йО- Скорректируйте этот дифференциатор на максимальную частоту дифференцируемого сигнала 1 кГц. (б) Рассчитайте вид выходного сигнала, если на вход дифференциатора подаются треугольные колебания частотой 1 кГц и амплитудой 2,5 В. Проверьте резу.аьтат расчета измерение^! выходного сигнала, (в) Подобрав надлежащим образом 7?к и С„, постройте на основе скорректированного дифференциатора полосовой фильтр с частотной характеристикой, показанной на рис. 6.29. Проверьте деГствке этого фильтра путем измерения выход-