6.8. ТРЕХРЕЖИМНЫЙ ИНТЕГРАТОР

Любой интегратор, предназначенный для интегрирования в течение длительных периодов времени, необходимо периодически сбрасывать в некоторое заданное начальное состояние (например, в нулевое). Кроме того, желательно иметь возможность останавливать на некоторое время изменение вы.\одного напряжения (режим фиксации); это дает возможность последовательно считывать несколько значений выходного напряжения и гарантирует неизменность выходного напряжения в тече-

R С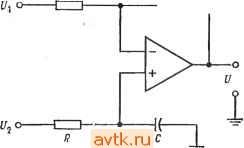

вых

Рис. 6.11. Разностный интегратор.

ние времени, необходимого для такого считывания. Трехрежим-ный интегратор, схема которого показана на рис. 6.12, обеспечивает возможность производить интегрирование, фиксировать выходной сигнал и периодически сбрасывать интегратор в исходное состояние. Схема имеет следующие режимы: Рабочий - собственно интегрирования.

Фиксации (хранения) - в течение определенного интервала времени выходной сигнал не меняется.

Установка начальных условий (или сброс)-интегратор возвращается в исходное состояние.

В рабочем режиме интегрирование производится обычным образом, и в качестве трехрежимного может быть использован любой из описанных в этой главе интеграторов. При большой длительности интегрирования накапливается большая ошибка За счет интегрирования тока смещения и напряжения сдвига и утечки через конденсатор. Максимальное время непрерывной работы интегратора определяется величиной суммарной ошибки, допустимой в данном конкретном применении. В рабочем режиме сигнал на выходе схемы рис. 6.12 имеет вид

(6.9)

/вых = -(1 ?0 51 + н.,

Ограничение

-о

Рис. 6.1ё. Трехрежимный интегратор.

где С7н. с - значение, которое выходное напряжение интегратора принимает в режиме сброса. Это напряжение сброса равно

Un.c==-{RB/RA)UB. (6.10)

Напряжение сброса равно нулю, если Ub = 0. Максимальное время, в течение которого интегратор может непрерывно работать, можно найти следующим образом. Так как С = It/U, а t = CU/I, имеем

раб. макс ~ CUqyoI 1ск>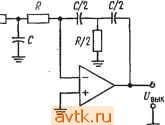

6.9. ДВОЙНОЕ ИНТЕГРИРОВАНИЕ

Используя Т-образный фильтр низких частот в каче- Рис. 6.13. Двойной интегритор. стве входной цепи интегратора [/= L rr at.

и Т-образный фильтр верхних частот в цепи обратной связи,

можно производить двойное интегрирование. Соответствующая схема показана на рис. 6.13. Выходное напряжение на выходе

) Автор приводит оценку /раб. макс ДЛЯ случэя, когда лимитирующим фактором является /см (это обычно свойственно биполярным ОУ). Нетрудно заметить, что в ОУ с ПТ-входом Uct будет лимитировать /раб. мам. - Прим. ред.

) Время выдержки, так же как и рабочее время, лимитируется обычно арядом С от /см. - Прим. ред.

где /см -ток смещения операционного усилителя, f/ош -максимально допустимое напряжение ошибки).

В режиме выдержки (хранения) входное сопротивление отсоединяется от интегратора, как показано на рис. 6.12. При этом напряжение на конденсаторе остается практически постоянным, так как входное сопротивление операционного усилителя весьма велико. Однако это напряжение не будет удерживаться на конденсаторе бесконечно долго, потому что ни входное сопротивление усилителя, ни собственное сопротивление конденсатора не бесконечны. Если последнее очень велико, то напряжение на конденсаторе будет экспоненциально падать с постоянной времени т АСЯ^к.у обычно весьма большой ).

В режиме сброс конденсатор вынужден зарядиться или разрядиться до напряжения, определяемого цепью обратной связи Ra и Rb- Р1апряжение на конденсаторе получает значение

U .c=-iRB/RA)VB.

Желательно, чтобы сброс происходил достаточно быстро, поэтому Ra и Rb выбираются настолько малыми, насколько позволяет усилитель. При этом время, необходимое для сброса интегратора, примерно равно IRbC Сопротивление Rb не следует выбирать настолько низким, чтобы ток разряда конденсатора мог повредить переключатели или контакты реле, используемые для выбора режима работы.

В качестве ключей или реле для выбора режима работы можно использовать ключи на биполярных или полевых транзисторах.

ДВОЙНОГО интегратора имеет вид

f/вых =-[4/(5 5 f/, Л.

(6.11)

Эту схему можно использовать для решения дифференциальных уравнений вида {dx/dt)-{- ах = f{t).

Если выход двойного интегратора соединить с его входом, то получится генератор с фазосдвигаюшей цепью, имеющий частоту самовозбуждения

f=mnR{C/2).- (6.12)

Пример 6.6. Двойной интегратор предназначен для использования в качестве генератора на частоте 1 кГц; выбрано С = 0,01 мкФ. Вычислить R. Решение:. Из выражения f = 1/2лР(С/2) следует, что Р = l/2nf(C/2) = = 1/6,28(1 кГц) (0,005 мкФ) = 3,18 кОм. Необходимые компоненты для построения схемы: С == 0,01 мкФ, С/2 == 0,005 мкФ, R = 3,18 кОм, Р/2 = 1,59 кОм.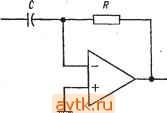

6.10. ДИФФЕРЕНЦИАТОР

Дифференциатор, показанный на рис. 6.14, создает выходное напряжение, пропорциональное скорости изменения входного. При дифференцировании усилитель должен пропускать

только переменную составляющую входного напряжения и коэффициент усиления дифференцирующей схемы должен возрастать при увеличении скорости изменения входного сиг--о нала. Выполнить эти требова-£/вых ния позволяет использование о в качестве входного элемента операционного усилителя кон-денсатора С. Чтобы получить выражение для выходного напряжения, вспомним, что ток через конденсатор имеет вид ic - C{dUc/dt). Напряжение на конденсаторе, естественно, равно входному напряжению Ui. Если предположить, что операционный усилитель идеален, то ток через сопротивление обратной связи можно считать равным току через конденсатор, т. е. ir = -ic. Но f/вых = Rir - = --ic/?, поэтому

UBux-RC{dUi/dt). (6.13)

Уменьшение реактивного сопротивления Хс с увеличением частоты приводит к тому, что схема дифференциатора имеет

Рис. 6.14. Дифференциатор. -вых^-4-f)-

ВЫСОКИЙ коэффициент усиления по отношению к высокочастотным составляющим на входе, даже если их частоты лежат выше полосы частот полезного сигнала. Поэтому наряду с высокочастотными составляющими спектра полезного входного сигнала схема усиливает собственные шумы сопротивлений и полупроводниковых элементов. Кроме того, эта схема имеет

ч

Частота, Гц

Рис. 6.15. Частотная характеристика нескорректированного диффе-

ренциатора.

Тонкая линия - коэффициент усиления без обратной связи; жирная линия - характеристика дифференциатора.

тенденцию к потере устойчивости в той области частот, где частотная характеристика дифференциатора (имеющая подъем Ъ дБ/октава) пересекается с имеющей спад 6 дБ/октава характеристикой скорректированного усилителя (рис. 6.15). Это означает, что частотная характеристика разомкнутого контура обратной связи имеет в некоторой части своего частотного диапазона спад 12 дБ/октава; при этих условиях, как было указано выше, вполне возможно самовозбуждение.

6.11. СТАБИЛИЗАЦИЯ ДИФФЕРЕНЦИАТОРА

Чтобы избежать проявления только что описанных нежелательных свойств дифференциатора, принимаются меры по его динамической стабилизации. Рис. 6.16 иллюстрирует эти меры.

Конденсатор Ск выбирается таким образом, чтобы участок характеристики со спадом 6 дБ/октава начинался на частоте более высокой, чем максимальная частота полезного дифференцируемого сигнала; при э.том уменьшается доля высокочастот-

ных шумов в выходном сигнале. Этот участок характеристики начинается на частоте

/2=1/2п/?Ск. (6.14)

Сопротивление Rk ограничивает коэффициент усиления на высоких частотах, обеспечивает динамическую устойчивость и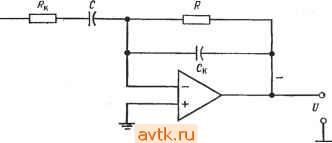

вых

Рис. 6.16. Скорректированный дифференциатор.

снижает входной емкостной ток схемы, отбираемый от источника сигнала. Действие коррекции на частотную характеристику дифференциатора показано на рис. 6.17. Добавление к схеме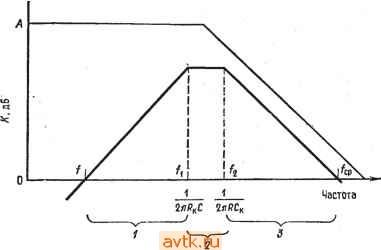

Рис. 6.17. Частотная характеристика скорректированного дифференциатора.

Тонкая линия - характеристика без обратной связи; жирная линия -характеристика дифференциатора. f=l/2ni?C, fj = l/2ni?C. Горизонтальные скобки внизу чертежа отмечают диапазоны частот, в которых происходят (i) дифференцирование (слева) и (3) интегрирование (справа) и (2) полосу пропускания фильтра (в середине).

сопротивления Rk приводит к появлению на частотной характеристике горизонтального участка и к прекращению дифферен-дирования на частотах, превышающих частоту

/1 = 1/2л/?кС. (6.15)

Следует отметить, что схема на рис. 6.16 выглядит как скорректированный интегратор со связью по переменному току, а из рис. 6.17 видно, что в полосе частот от f2 = 1/2лкСк и до частоты fcp схема представляет собой интегратор. В полосе частот от / до /i = 1/2л/?кС схема является устойчивым дифференциатором. Частоту fl = 1/2л/?кС следует задавать возможно

Таблица 6.1. Зависимость погрешности дифференциатора от частоты fi )

) Указана рабочая частота в долях fi. -Прим.

более низкой при заданных полосе частот полезного сигнала и точности дифференцирования. Зависимость погрешности от частоты fl = 1/2якС дана в табл. 6.1.

Rk и Ск часто выбирают так, чтобы RkC = RCk и fi = /2-Как и в случае интегратора, наилучшие результаты получаются при использовании в дифференциаторе тефлоновых или .полистироловых конденсаторов (на более высоких частотах пригодны также майларовые конденсаторы) и малошумящих сопротивлений на металлической пленке. В случаях когда имеет значение время возвращения схемы в исходное состояние (после перегрузок), могут оказаться полезными схемы ограничения.

€.12. СКОРРЕКТИРОВАННЫЙ ДИФФЕРЕНЦИАТОР КАК ЧАСТОТНЫЙ ФИЛЬТР

Следует отметить, что частотная характеристика (рис. 6.17) скорректированного дифференциатора является характеристикой активного полосового фильтра с крутизной склонов 6 дБ/ок-тава. Поэтому схему скорректированного дифференциатора можно использовать в качестве полосового фильтра с полосой пропускания между /1 = 1/2л:/?кС и /2 = \/2nRCy, если полосой пропускания считать интервал частот, в котором коэффициент

усиления постоянен. В этом диапазоне частот коэффициент усиления оказывается приблизительно равным R/Rk..

Пример 6.7. Дифференциатор предназначен для использования в качестве полосового фильтра с fi = 1 кГц, f2 = 5 кГц и 7( = 30. Найти R, С, Ск и /?к. Решение: Так как К = Р/Рк, сначала следует выбрать Р или Рк. Положим Р = 30 кОм, тогда Рк = Р/К = 30 кОм/30 = 1 кОм.

Из соотношения - \12пРкС находим С = ll2nPfi = l/2n(l кОм)(1 кГц) = = 0,159 мкФ.

Аналогично fs = l/2n/?C и Ск =--l/2nRf2 = l/2n( 30 кОм) ( 5 кГц) = = 0,0011 мкФ.

Итак, Р = 30 кОм, Рк = 1 кОм, С = 0,159 мкФ и Ск == 0,0011 мкФ.

Скорректированный дифференциатор можно использовать и в качестве заграждающего полосового фильтра, если подклю-ff, /?05 чить его к одному из вхо-

дов сумматора, как показано на рис. 6.18. При этом часть сигнала, проходящая через полосовой фильтр, будет взаимно уничтожаться с соответствующей частью сигнала проходящего через сопротивление Ru эта часть сигнала лежит в полосе частот фильтра пропускания. Последний должен инвертировать сигнал,что скорректированный дифференциатор фактически и делает, а сумматор, для

--С

:вых

Рис. 6.18. Заграждающий полосовой фильтр.

В разрыве перед. Кг - нивертнрующнй полосовой фильтр.

того чтобы заграждение было эффективным, должен быть построен так, чтобы выполнялось условие

= коэффициент усиления полосового фильтра -1--. (6.16)i

Если частоту f2 = 1/2зг/?Ск задать много большей, чем fi = = 1/2л/?кС, то скорректированный дифференциатор можно использовать в качестве фильтра верхних частот с коэффициентом усиления, равным R/Rk-

6.13. ДЕЙСТВИЕ ДИФФЕРЕНЦИАТОРА НА НЕКОТОРЫЕ ТИПЫ СИГНАЛОВ

Поучительно рассмотреть вид выходных сигналов дифференциатора при подаче на его вход некоторых стандартных сигналов. Проделаем это на нескольких примерах.

Пример 6.8. В дифференциаторе на рис. 6.16 R = 0,1 МОм, С = 0,1 мкФ, а Лк и Ск выбраны таким образом, чтобы стабилизировать схему. На вход подается синусоидальное напряжение амплитудой 3 В и частотой 60 Гц, т. е. {/= (3 B) sin 2n(60)/. Каковы величина и форма выходного напряжения? Решение:

О'е... = -RC-RC (ЗВ-32.(60)/)

поэтому f/вых = -лез[2я(60)]COS 2л;(60)/. Таким образом, напряжение на выходе изменяется по закону косинуса, чего и г,чедовало ожидать, так как

+4 В -

О

-4В

а

Рис. 6.19. Реакция дифференциатора на треугольный входной сигнал. а - входной сигнал, f = 1 кГц; б - выходной сигнал, f = 1 кГц.

ds.nu = COS и du. Величина выходного напряжения равна f/вык = = (0,01) (3 В)120ясо5 2яД = -(11,31 В)со52яД.

Пример 6.9. В дифференциаторе на рис. 6.16 R= 10 кОм, С = 0,1 мкФ, а Rk и Ск обеспечивают динамическую стабилизацию. На вход дифференциатора подается треугольная волна, показанная на рис. 6.19. а. Каким будет выходной сигнал?

Решение: Рассмотрим входное напряжение как функцию времени. Так как этот сигнал является симметричной периодической волной, достаточно построить выходное напряжение для одного полупериода. Выходное напряжение для следующего полупериода будет иметь ту же форму, но с противоположной полярностью. Так как входное напряжение линейно растет до значения 2 В в течение 0,5 мс, можно написать f/вых =.(2 В/0,5 мс)/ = = (4-10 В/с)/, где /-время в секундах. Посколтку дифференциатор реагирует только на изменения напряжения, можно пренебречь постоянной составляющей входного сигнала. Теперь найдем вид выходного напряжения, ноль-, зуясь выражением (6.13):

г/ ,= =- ЛС (4 103 В/с) =

= - (10 кОм) (0,1 мкФ) (4 10 В/с) = - (0,001 с) (4 10 В/с) = - 4 В.

Таким образом, выходной сигнал - это прямоугольная волна амплитудой 4 В (или размахом 8 В), частота которой равна частоте входного сигнала; выходной сигнал показан иа рис. 6.19,6. Из этого примера можно сделать об-Щлй вывод, что любому линейно изменяющемуся сигналу на входе дифференциатора соответствует постоянный выходной сигнал, величина которого пропорциональна крутизне входного сигнала; этот выходной сигнал остается

постоянным в течение всего времени, пока входной сигнал сохраняет постоянный наклон.

Пример 6.10. На вход дифференциатора из примера 6.9 подается прямоугольная волна с амплитудой 5 В н частотой следования 5 кГц, причем времена нарастания и спада импульсов равны 1 мкс. Изобразить выходной сигнал. Решение: Входной сигнал, изображенный на рис. 6.20, а, следует разбить на части и дифференцировать раздельно. Участки входного сигнала, на которых:

вык.макс

-и

л h Время

вых.макс

Время:

а

Рис. 6.20. Выходной сигнал дифференциатора при прямоугольной волне на

а - входной сигнал, частота следования 5 кГц, н~с ° б - выходной сигнал.

частота следования 5 кГц.

его значение постоянно и равно 5 илн О В, не дают никакого напряжения на выходе дифференциатора, так как производная постоянной величины равна нулю. Участки нарастания и спада импульсов можно аппроксимировать наклонными прямыми. Поскольку / = с, выходное напряжение во время нарастания равно выходному напряжению во время спада и противоположно ему по знаку; легко видеть, что ненулевое выходное напряжение вообще появляется только во время спада или нарастания импульсов.

Для нахождения t/вых во время нарастания или спада надо сначала выразить эти участки входного сигнала как функции времени. Имеем =, г= <е = (5 В/1 мкс) / = (5-10 = B/c)i.

Теперь, используя выражение (6.13), получаем

С/в

= - PC (dUBKldt) = -рС(5-10 В/с) =

= (0,001) (-5 10 В/с) = - 5 10 В

во время нарастания и t/вых = -f-5-lO В во время спада. Операционный усилитель, способный давать на выходе 5 кВ, представлял бы собой весьма необычное явление. Выходной сигнал реального ОУ будет состоять из двух Hfi пульсов противоположной полярности длительностью 1 мкс, амплитуда которых равна максимально возможному выходному напряжению операционного усилителя или напряжению ограничения, если в схеме используется схема ограничения. Как уже было указано в разд. 6.4, использование схемы ограничения для уменьшения времени восстановления желательно в большинстве схем дифференциаторов ).

) Практически очень трудно сделать схему ограничения с быстродействием, необходимым в этом примере. - Прим. ред.