обратной связи достаточно велик, так что Ug О, получим j, = Ui/Ri, h = U2/R2, h == U3/R3 и to. с -Ubmx/Ro. с, откуда Ui/Ri + U2/R2 + U3/R3 = -Ubux/Ro. с Решая это уравнение относительно t/вых, получаем

вых = - (Ro. c ?i) +1/2 (Ro. JR2) 4-t/3 (Ro. c/Rs)] (5.3)

Пример 5.2. Найти и^ых, если на рис. 5.2 Ri = 20 кОм, R2 = 50 кОм, Rs = = 25 кОм и /?с. с == 100 кОм и если f/i = I В, U- = 2 В и t/g = -3 В.

f/вых = - Wi (Ro. c/Ri) + £/2 (i?o. c ?2) + (Ro. clRs)\ =

[- / iookomn / 100 kom n /- 100 кОм чт

.Uo kom j+v 50kom 25 кОм j.

=-[1B(5)-Ь2В(2) - 3B(4)] = -(5B-b 4B - 12B) = (-3B) = 3B.

Пример 5.3. Найти Ri, R2 и Rs, такие, чтобы в схеме на рис. 5.2 С/вых = = - (6(/, + 3t/2 -Ь 4t/3), Ro. с = 200 кОм.

Решение. Рассмотрим коэффициенты усиления отдельно для каждого входа.

Эти коэффициенты усиления должны быть соответственно равны: 6 для входа t/ (/,£> 3 для входа Hi к А для входа f/з. Разрешая относительно Ri соотношение Ot/i = t/i (Rc. JRi), получим Rl = /?о. с/6 =

= 200 кОм/6 = 33,3 кОм.

Аналогично получим R2 = = 200 кОм/3 = 66,6 кОм и Rs = 200 кОм/4 = 50 кОм. Такой анализ схемы суммирования с масштабными коэффициентами можно обобщить на случай схемы с п входами, в результате чего получится соотношение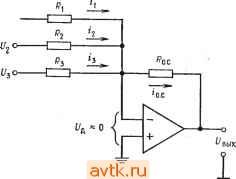

Рнс. 5.2. Схема суммирования с масштабными коэффициентами.

i/вых = (Ro.dRi) +

+ U2 (Ro.clR2)+ ... +

+ Un(Ro.c/Rn)]. (5.3а) Схема усреднения. Если в схеме на рис. 5.2 положить Ri = R2 = Рз = ... ... = /? и /?о. с == Ri/n, где - число входов схемы, получим

f/вых =-(U, + U2 + Us+ ... + Un)ln. (5.4а)

Другими словами, такая схема окажется схемой усреднения. Чтобы в этом убедиться, заметим, что --Ubux/Ro. с = CJi/R\ -f- UzR2-{... \-VnjRn, откуда

f/вых =-Ro.c [(f/. + U2+... + UnVRl].

Ho Ro.c = Ri/h, поэтому

r, Rl r fJl + U2+ ...+Un\ Ui+U2+ ...+Un

ивы. = --[ Wi j= n

Пример 5.4. Построить схему на рис. 5.2 таким образом, чтобы она осуществляла усреднение трех входных сигналов.

Решение: Положим /?, = = R3 = 200 кОм и /?о. с = R\ln, т. е. 200 кОм/3= = 66,6 кОм. Отметим, что в схеме усреднения Ro. с = /?il/?2ll Wn, что позволяет осуществить усреднение с весами. Под усреднением с весами подразумевается, например, такая операция:

0 = - +2Ui + Ui + + г/ )/число входов].

Собственно говоря, схема усреднения - это всего лишь частный случай инвертирующего сумматора.

Замечание. Сопротивление в цепи обратной связи выбирается таким образом, чтобы ток обратной связи был много больше тока смещения операционного усилителя и в то же время не превышал значений, которые усилитель мог бы легко обеспечить вместе с необходимым током нагрузки. Для большинства операционных усилителей диапазон возможных значений сопротивления обратной связи доста.очно широк.

5.3. СХЕМА СЛОЖЕНИЯ-ВЫЧИТАНИЯ

Схема сложения-вычитания показана на рис. 5.3. Эта схема представляет собой обобщение показанной на рис. 1.11 схемы

Инвертирующие входы

Неинвертирую-щие входы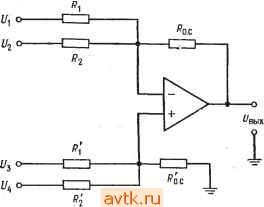

Рис. 5.3. Схема сложения-вычитания, если H-R / = ; JR .

усилителя с дифференциальным входом. Общее выражение для выходного напряжения схемы сложения-вычитания очень громоздкое, поэтому мы рассмотрим только условия, выполнение которых необходимо для правильной работы этой схемы.

Эти условия сводятся, в сущности, к тому, чтобы сумма коэффициентов усиления инвертирующей части схемы была равна сумме коэффициентов усиления ее неинвертирующей части.

Другими словами, инвертирующий и неинвертирующий коэффициенты усиления должны быть сбалансированны

Символически это можно обозначать следующим образом;

о. с I I о. с о. с I о. с I I о. с

Rl R2 Rm 1 2

где tn - число инвертирующих входов, а п - число неинверти-рующих; отсюда имеем

Сказанное можно пояснить следующими примерами: Пример 5.5. Пусть в схеме на рис. 5.3 t/j = t/j = 1 В, Us = U4 = 2 В, с = 200 кОм, r с = 100 кОм, /?, = 100 кОм, R = 25 кОм, Rs = 25 кОм и /?4 = 16,67 кОм. (а) Выполняется ли условие баланса? (б) Чему равно

Решение: (а) Проверим баланс.

£l + :?li = . + -. 200 кОм 200 кОм ? ..

/?, /?2 . /?[ /?2 100 кОм 25кОм ? 100 кОм , 100 кОм

=-25W+ 16,67 кОм= 2 + 8=10 = 4 + 6=10.

Таким образом, баланс имеет место. .

(б) Используя соотношение (5.5), получим

= 2В (4) + 2В (6) - IB (2) - IB т поэтому 1/вь,х = 8 В + 12 В-2 В-8 В = 20 В-10 В = 10 В. Пример 5.6. В схеме на рис. 5.3 Ri = R2= Ri = Rz = Ro. с = o. с- Написать выражение для t/вых.

Решение: Используя выражение (5.5), получим t/g, = U JRi) + t/4 X X c/?2) - t/i (/?o. c/i)~2 (o. c/2)- Поскольку здесь все сопротивления одинаковы, обозначим их одной буквой R и получим t/вых = t/3 (/? ?) + + t/4(/? ?) - UiiRIR) - t/2(/? ?) = (6-3+ t/4) - (t/, + t/2). Проверка выполнения условия баланса предоставляется читателю.

) Под неинвертир>тощими коэффициентами усиления автор подразумевает' отношение резисторов на неинвертирующем входе (см. ниже), которое будет равно усилению по этому входу только при условии баланса.- Прим. ред.

В Примере 5.5 мы имели дело с готовой схемой, баланс которой уже был обеспечен. Возникает вопрос, как обеспечить баланс в схеме, которую мы конструируем заново? Оказывается, схему можно сделать балансной, добавив к ней дополнительный вход, на который подается нулевой сигнал. Этот

/?, = 25 кОм о-1 I-

/?2 = 50 кОм

Ux= ОБ

Г

/?х=20 кОм

/?ас = 100 кОм

/?, = 10 кОм

вык о

/?о.с = 100 кОм

1/4 о-1-1-

/?г = 100 нОм

Рис. 5.4. Сбалансированная схема сложения-вычитания.

вход добавляется к той половине усилителя, суммарный коэффициент усиления которой меньше. Применение такого способа показано в примере 5.7.

Пример 5.7. Построить схему сложения-вычитания так, чтобы напряжение на ее выходе было равно t/вых = -4t/ - 2t/2lOt/3-f-

Решение: Целесообразно положить Ro.c - Ro. с поэтому выберем р^ = =Ro. с = 100 кОм. Для нахождения Р^, R2, р[ и R2 можно- использовать соотношение (5.5) в форме, приведенной на рис. 5.3, так как данная схема имеет всего четыре входа.

Коэффициент при Ui равен Ro. dRi - 4, поэтому Ri = Ro с/4 = = 100 кОм/4 = 25 кОм.

Аналогично /2 = 2; R = R J2 = 100 кОм/2 = 50 кОм; r[ = r JlO = = 100кОм/10= 10 кОм;/?2 =/?о c/l = 100кОм/1 = 100 кОм. Проверяя наличие баланса, мы видим, что Р^ /Р^ + Р^ JR2 = 4 -[- 2 = 6 и Ro.c/Ri +

+ с/2= 10 -1- 1 == И, т. е. сумма неинвертируюших коэффициентов усиления на пять больше суммы инвертирующих коэффициентов. Если изменить схему таким образом, чтобы напряжение на ее выходе стало равным f выя = = - (4t/i--2t/2-l-5t/x)-1-(10(Уз--f,), и задать Ux = 0, то полученное выходное напряжение окажется равным желаемому. Нам остается подключить

к инвертирующему входу, как показано на рис. 5.4, такое сопротивление Rx, чтобы отнощение Ro. c/Rx было равно 5, и тогда баланс схемы будет обеспечен. Величина Rx равна Ro. с/5 = 20 кОм. В полученной схеме Ro. jRi 4-

+о. + Ro. c/Rx = ro. c/Ri+Ro. JrI или 4 + 2 -Ь 5 = 11 = 10 I -= 11.

так что схема будет действовать нормально. Если бы суммарный коэффициент усиления неинвертирующей половины усилителя оказался меньшйиГ, то следовало бы подключить сопротивление /?. между неинвертирующим входом

и землей; величина этого сопротивлешя, обеспечивающая баланс схемы, определяется аналогичным образом.

Отметим, что для обеспечения устойчивости схемы сумма коэффициентов усиления каждой из половин усилителя должна быть не меньше единицы, если только нам не известно заранее, что данный усилитель работает устойчиво при /С < 1.

S.4. НЕИНВЕРТИРУЮЩИЙ СУММАТОР

Для осуществления простого суммирования, при котором i/вых == t/i + + ... + t/n, можно построить спсциальный вариант схемы сложения-вычитания. Предположим, что нам надо

Рис. 5.5. Неинвертирующий сумматор с двумя входами.

*о.с/ 1=<.с/ ><.с/ 2

о. с 1

р^ = т ком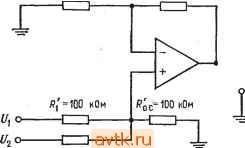

/?2 = 100 кОм

получить [/вых =Ui + [/г- Зададим R = R[ = R и /?, = R Jn,

где п - число входов (в данном случае два). Такая схема показана на рис. 5.5.

Мы можем также осуществить суммирование с весами; например, можно сформировать t/вых = f/i-Ь 2[/2. Обязательно Только соблюдение условия

Лля п входов.

о. с (

+ ... -f

114 Главам

5.5. РЕШЕНИЕ СИСТЕМЫ УРАВНЕНИЙ

Ранее в этой главе мы упоминали, что суммирующие схемы можно использовать для решения систем уравнений. Способ их решения мы сейчас продемонстрируем на примере, в котором будет использована схема сложения-вычитания.

Пример 5.8. Решить относительно X и Y систему уравнений: (а) 2Х + 3Y = = 40; (б) 2 -f У = 5.

Решение: Прежде всего надо выбрать масштаб, в котором могут быть представлены все возможные ответы при тех значениях коэффициентов, которые мы собираемся использовать. Если, например, выходное напряжение операционного усилителя может меняться в пределах ±15 В, а и У никогда не превышают 150, то мы можем выбрать масштаб 0,1 В = 1. При этом числу X - 1Ъ будет соответствовать напряжение 1,5 В на выходе X. В этом примере будет использован масштаб 0,1 В = 1. Для определения пределов, в которых могут меняться переменные, можно решить систему уравнений алгебраически. Эта возможность не делает схему для решения систем уравнений ненужной, так как последняя обычно используется в схемах управления, где-необходимо формировать непрерывное решение'). Если пределы изменения переменных превысят допустимые пределы выходного напряжения, то следует-изменить масштаб таким образом, чтобы ответ всегда попадал в эти пределы.

Теперь мы решим одно из уравнений относительно X, а другое относительно У. Решая (а) относительно X, пол>чим Х= (40 - ЗУ)/2 =20-1,5У.. Решая (б) относительно У, находим, что У = -2Х + 5. Теперь построим первую схему сложения-вычитания, выходной сигнал которой равен X, так что

- = 20 . е/0-(о.с/.)1-

Положительные числа мы будем подавать иа неинвертирующую половину схемы, а отрицательные - на инвертирую1д>то. Двадцать - положительное число, поэтому мы подадим его с коэффициентом усиления, равным единице, на неинвертирующую половину. Для того чтобы этот коэффициент усиления был равен единице, нам надо положить Р^ = Ру. Положим также-для удобства /?о. с = о. с- Так как - 1,5У = (?o. c ?i) У, имеем Ri - о. с/1>5- Положим = р^ = 100 кОм; тогда получим Р^ с = о. с -

= pi 100 кОм и /?1 = 100 кОм/1,5 = 66,7 кОм.

Теперь включим первый усилитель в соответствии со схемой на рис. 5.6. Отметим, что к неинвертирующему входу схемы подключено дополнительное сопротивление /?, такое, что р' Jр' = 0,5; в результате оба коэффициента усиления (инвертирующий и неинвертирующий) оказываются равными 1,5.

Построим еще один усилитель для нахождения У. Поскольку У^= -2Х + -{ 5, должно выполняться равенство У = (- Р^ JPj) Х+ 5 (/?о c/i) поэтому

о.с ?1 = 2 и <.еК=1.

Если положить Рд = р' = 100 кОм, то найдем, что Ру - 100 кОм/2 =

= 50 кОм и pi = 100 кОм/1 = 100 кОм.

Инвертирующий коэффициент усиления такой схемы равен 2, а неинвертирующий равен 1. Для получения баланса надо добавить к неинвертирующей половине схемы нулевой вход с коэффициентом усиления, равным единице, так что Ро. с/х -

) Имеется в виду решение при условии изменения правых частей. Прим. ред.

Легко заметить, что = 100 кОм Теперь можем построить схему формирования У, которая показана на рис. 5.7.

Теперь для решения исходной системы уравнения остается только со-единить выход усилителя, формир>тошего X, с Х-входом усилителя, форми-

/? = 66,7к0м /?о.с=100кОм

Рис. 5.6. Схема для вычисления X = 20 - 1,5 У.

0 - 2 В при масштабе 1 в =- Ю; О = О В на балансировочном входе. У - это выходной сигнал усилителя, решающего уравнение относительно Y (рнс. 5.7).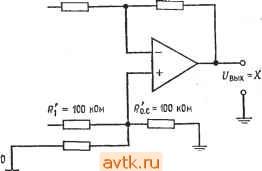

20 0

Rx = 200 кОм

дующего У, а выход последнего соединить с У-входом усилителя, формир>то-вдего X. Ответы можно прочитать на соответствующих выходах. Полная схема для решения системы уравнений показана на рис. 5.8.

Укажем, что для решения системы трех уравнений с тремя леизвеетными потребовались бы три схемы сложения-вычита-лия с тремя входами каждая.

/?, = 50 кОм /?ох = 100 кОм

Рис. 5.7. Схема для вычисления У = -2Х + 5.

- выходной сигнал усилителя, решающего уравнение относительно x (рис. 5.6). 5 = 0,5 В при масштабе i В = 10; О - О В на балансировочном входе.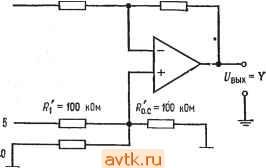

rx = 100 кОм

Системы уравнений можно решать, используя только инверторы и инвертирующие сумматоры. В этом случае необходимое количество усилителей часто оказывается большим, чем в случае использования схем сложения-вычитания, но зато уничтожается синфазная ошибка и снимается проблема обеспечения баланса. Этот способ ясен из рис. 5.9, где приведена схема для Решения системы уравнений из примера 5.8. Следует отметить.

/?, =66,7к0м /?о.с=100кОм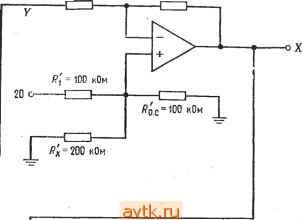

/?, = 50 кОм ;?о,с=100кОм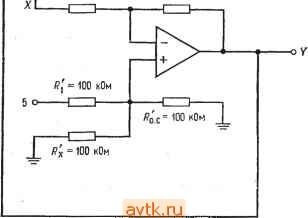

Рис. 5.8. Схема для решения системы уравнений- 2А: + ЗУ = 40 и-2X+Y = 5.

Вверху -схема вычисления выражения x = 20 - л.ьу (рис. 5.6); внизу - схема-вычисления выражения y = = -2х + 5 (рпс. 5.7). Ответ: x - 6,25 - 0.625 В и У = = 17,5 = 1.75 В.

ЧТО некоторые из входов имеют полярность, противоположную-их знаку в уравнениях. Это нужно для обеспечения правильной полярности на входе инвертирующего сумматора. Например, для получения на выходе инвертирующего сумматора величины X приходится подавать на его вход -X, а для получения числа 5 надо подать на вход -5 .

) В схемах описанных типов могут возникать петли положительной обратной связи и неустойчивость, связанная со сдвигом фазы. В частности приведенные примеры схем вряд ли работоспособны, -г Прим. ред.

/?, = 66.7 кОм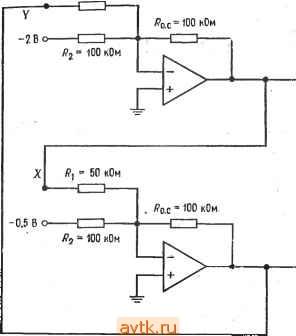

оХ = 20-1.5У

oV -2Х+5

Рис. 5.9. Схема для решения системы уравнений 2X + 3Y = 40 и 2Х + У = 5, использующая только инвертирующие усилители.

Вверху -схема вычисления x = 20 - l,5y; внизу -схема вычисления y = = -2х + 5. Масштаб: 1 В = 10.

5-6. ПРОПОРЦИОНАЛЬНОЕ УПРАВЛЕНИЕ

Суммирующие схемы на операционных усилителях идеальны в качестве схем пропорционального регулирования. Системой пропорционального регулирования называется схема, выходное-напряжение (т. е. напряжение, подаваемое на управляемый элемент или объект управления) которой пропорционально разности напряжения уставки (указывает об1: кту управления, что надо делать) и напряжения, характеризующего состояния объекта управления (которое показывает, что в действительности делает управляемый об1зект).

- Принцип действия системы пропорционального регулирования мы проиллюстрируем на примере системы регулирования скорости электродвигателя постоянного тока, схема которой показана на рис. 5.10. Эта система включает следующие основные элементы: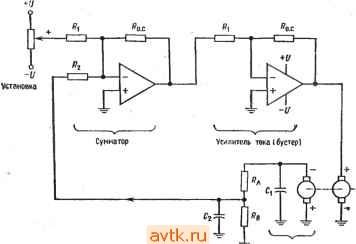

Harpv3Ka доигателя

Тахометр Электродвигатель (обратная пост, тока с ceesb) поп, магнитом

Рис. 5.10. Пример системы пропорционального регулирования: схема

управления скоростью вращения двигателя постоянного тока.

Напряжение уставки задает желательные скорость и направление вращения. Отслеженное напряжение характеризует действительные скорость и направление вращения

двигателя.

1. Напряжение уставки указывает, в каком направлении и с какой скоростью мотор должен вращаться. Амплитуда управляющего напряжения задает, как быстро мотор должен вращаться, а полярность управляющего напряжения указывает направление его вращения.

2. Суммирующая схема сравнивает напряжение уставки с отслеживаемым напряжением и формирует выходное напряжение, пропорциональное разности уставки и отслеживаемого напряжения. Это напряжение (разность) называется напряжением ошибки.

3. Усилитель (бустер) тока, который часто называют еще сервоусилителем, обеспечивает напряжение питания двигателя при достаточном для его действия токе. В нашей системе двигатель

должен иметь возможность изменять направление вращения, поэтому усилитель тока должен задавать как положительные, так и отрицательные напряжения питания двигателя. Сейчас нас интересует только способность этой схемы обеспечивать необходимые для работы двигателя напряжения и токи, а не ее конкретное устройство. В качестве сервоусилителя можно взять, например, операционный усилитель с токовым бустером тока

-Вроде тех, которые описаны в гл. 9.