Наибольшая величина или амплитуда магнитного потока, как это следует из выражения для мгновенного его значения, будет

-w,2f 4,44/w,

Из последнего равенства мы можем получить действующее значение электродвижущей силы, выраженной через амплитуду магнитного потока, а именно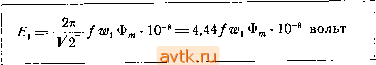

Так как электродвижущая сила во вторичной обмотке трансформатора индуктируется тем же магнитным потоком, что и электродвижущая сила в первичной обмотке, то можно сказать, что и вторичная электродвижущая сила меняется во времени по закону синуса. Действующее значение ее определится выражением

= -/2 Фт 10-* = 4,44/да, Ф, Ю * вольт

Коэфициент трансформации

Пусть, например, наибольшее значение магнитного потока трансформатора Ф„ = 0,8-10 максвелл, а число витков первичной и вторичной обмоток w,=5630 и , = 118. Определим электродвижущие силы El и Е^ при частоте /=50 Hz.

По вышеполученным формулам имеем:

£i = 4,44 50 5630 0,8 10 .10-= 10 ООО V; £, = 4,44 . 50- 118 0,8 . 10 . Ю * =210 V. Коэфициент трансформации

10000 .- = t = -Действующие значения электродвижущих сил и можно еще определить через средние их значения и через коэфициент формы кривой электродвижущих сил. Если -[-Ф„ и - Ф^ -наибольшие значения потока (см. рис. 62а), то полное изменение магнитного потока за полупериод 7/2 выразится разностью

-f Ф„-(-ФJ = 2Ф, .

Следовательно, средняя электродвижущая сила одного витка обмотки за тот же промежуток времени будет

2Ф Г/2

Так как -L=/, то

Обозначим отношение действующего значения электродвижущей силы одного витка ев к среднему значению электродвижущей силы вер через ke. Тогда

ед = есрка = Акв/Ф„.

Коэфициент ke называется коэфициентом формы кривой электродвижущей силы.

Действующие значения электродвижущих сил первичной и вторичной обмоток будут:

Ei=4ke fWi Ф„ 10 вольт;

= ake fw Ф„ 10~* вольт.

Для синусоиды коэфициент формы в = 1,11. Если подставить это значение в последние формулы, то получим ранее выведенные выражения для и Е^.

Для тупых кривых, подобных трапеции, коэфициент формы в<С1,11. а для острых кривых, подобных треугольнику, fee > 1,11.

Изучение работы трансформаторов производится обычно помощью векторных диаграмм. Если отказаться пока от рассмотрения побочных явлений, то упрощенная векторная диаграмма для случая, когда вторичная обмотка разомкнута, представится рис. 66а, на котором Оа-г вектор потока Ф; Ос и Od-векторы электродвижущих сил первичной и вторичной обмоток Ei и Е^, отложенные в сторону отставания на 90° от вектора потока; Ое - вектор приложенного к первичной обмотке напряжения уравновешивающего первичную электродвижущую силу.

С вегктором магнитного потока совпадает вектор Ob той магнитодвижущей силы, которая этот поток создает и которая равна 0,4it4wj, если через / обозначить ток в первичной обмотке. Тот же вектор Ob в другом масштабе может изображать намагничивающие ампервитки первичной обмотки IgWi или просто намагничивающий ток / ,

§ 21. Ток холостой работы трансформатора.

При разомкнутой вторичной обмотке электродвижущая сила, индуктирующаяся в первичной обмотке, почти равна по величине и прямо противоположна по направлению приложенному напряжению, так как она его уравновешивает. Ток в первичной обмотке создается только небольшою разностью между приложенным к ней напряжением К, и индуктируемой в ней же электродвижущей

силою El. Этот ток, так называемый ток холостой работы, у обычных трансформаторов относительно весьма мал (он равен 5-107о нормального тока). Для создания магнитного потока в замкнутом железном сердечнике с небольшим магнитным сопротивлением, при большом числе витков первичной обмотки, требуется незначительный намагничивающий ток.

При синусоидальном напряжении, приложенном к первичной обмотке, магнитный поток должен быть синусоидальным, так как только при синусоидальном потоке индуктируемая им электродвижущая сила может уравновесить приложенное синусоидальное напряжение. Казалось бы, что и намагничивающий ток должен быть синусоидальным. В действительности, однако, намагничивающий ток трансформатора далеко не синусоидален. Причинами этого обстоя-

тельств? являются:

1) способность железа., насыщаться, благодаря чему магнитный поток меняется не пропорционально намагничивающему току,

2) задерживающая или коорцетивная сила железа, проявляющая себя при переменном намаг^ иичении (гистерезис).

На рис-. 67а изображен известный шлейф гистерезиса , т. е, кривая abed, иллюстрирующая действительное изменение магнитного потока или индукции в железном сердечнике при изменении намагничивающей силы. По оси ординат на рис. 67а отложена индукция в железе сердечника В, а по оси абсцисс--число ампервитков, приходящихся на один сантиметр пути потока, т. е. awJcM. В другом масштабе мы могли бы отложить по оси ординат магнитный поток в сердечнике Ф, ибо Ф = BQ, где В - индукция, а Q - поперечное сечение сердечника; по оси же абсцисс мы могли бы отложить на-

магничивающий ток / , ибо-- = ада,/сл , где - число витков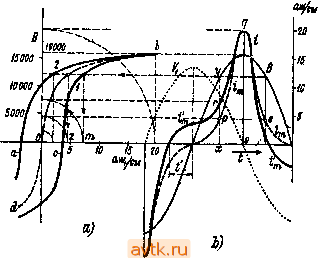

Рис. 67.

первичной, обмотки, а /-средняя длина пути магнитного потока.

На рис. 67Ь синусоида V, иллюстрирует изменение во времени приложенного к первичной обмотке напряжения, а кривая В иллюстрирует изменение во времени магнитной индукции (или магнитного потока) в сердечнике трансформатора. Масштаб для ординат кривой В тот же, что и для ординат шлейфа гистерезиса abed.

Предположим сначала, что гистерезис и токи Фуко в железе отсутствуют, а изменение индукции при изменении ампервитков намагничения происходит по кривой намагничения Obd. В таком случае для получения индукции, меняющейся во времени по синусоиде В, необходим намагничивающий ток, меняющийся по кривой (пунтирной) Эту кривую легко построить по кривым В и Obd. Например, для какого-либо момента времени х индукции ху соответствует По кривой Ob намагничивающие ампервитки Oz, которые в том же масштабе отложены по ординате ху в виде отрезка хр = = 0z (последовательный ход нахождения точек кривой i указан на рис. 67 стрелками). Из рис. 67 видно, что, благодаря свойству железа насыщаться, кривая намагничивающего тока, необходимого для создания синусоидальной индукции, в значительной степени отличается от синусоиды. Ее амплитуда совпадает, однако, с амплитудой кривой индукции В; точно так же совпадают и нулевые значения обеих кривых.

Под влиянием магнитного гистерезиса кривая намагничивающего тока несколько искажается. Если принять, что процесс переменного намагничения происходит по кривой abed, то синусоидальное изменение индукции будет иметь место только при намагничивающем токе, меняющемся бо времени по кривой (рис. 67Ь). Нахождение ординат этой кривой не отличается от нахождения ординат кривой i (см. на рис. 67 нахождение ординаты хг=От для индукции ху по ветви / кривой abed).

Из рисунка видно, что под влиянием гистерезиса кривая намагничивающего тока i! стала несимметричной. Хотя ее амплитуда совпадает с амплитудой кривой индукции, но нулевые значения смещены относительно соответствующих нулевых значений кривой индукции В в сторону опережения на некоторый промежуток времени t. Так как мягкое трансформаторное железо обладает весьма небольшою задерживающею силою, то опережение кривой намагничения относительно кривой индукции незначительно. Тем не менее это опережение говорит нам, что в данном случае (т. е. при наличии гистерезиса) намагчичивающий ток уже имеет активную составляющую, которая несет с собой из сети энергию для покрытия расхода энергии в железе на работу гистерезиса. Это видно из того, что кривая отстает по фазе от кривой напряжения V, на угол, меньший 90° (см. рис. 67). Реактивная составляющая намагничивающего тока, совпадающая по фазе с кривой индукции, является собственно намагничивающей. При переменном намагничении железа в нем наблюдается еще чисто электрическое явление: в массе железа индуктируются вторичные токи Фуко (см. далее), которые имеют следствием потери энергии в этой массе. Эгу энергию должен доставить первичной обмотке тот же намагничивающий ток своею дополнительною активною составляющей. Если на рис. 68а'нанести кривую активного тока 1ф, покрывающего потери, причиняемые токами Фуко в железе (кривая 1ф совпадает по фазе с кривой напряжения Vj), а затем ординаты этой кривой сложить с ординатами кривой намагничивающего тока i, то мы получим кривую действительного намагничивающего тока i (форма этой кривой под-

тверждается экспериментально). Из рис. 68а мы видим, что опережение кривой намагничивающего тока относительно кривой индукции под влиянием токов Фуко увеличилось и стало равным t . Иными словами, отставание намагничивающего тока от напряжения V, уменьшилось.

Кривая намагничивающего тока трансформатора как показывает рис. 68а, несинусоидальна. Но ее, как кривую периодическую, можно разложить на ряд синусоидальных кривых, а именно: на основную синусоиду (или основную гармонику), имеющую ту же периодичность, что и исходная кривая i, и на ряд синусоид или гармоник высшего порядка, т. е. имеющих высшие периодичности, нежели у действительной кривой. На рис. 68Ь приведены примерные составляющие кривой намагничивающего Т0К9 i: основная синусоида тока /, и кривая / , содержащая все остальные синусоиды высшего порядка. В виду специфической формы шлейфа гистерезиса, определяющей в основном форму кривой намагничивающего тока в этой кривой особенно ярко выражена третья гармоника и несколько, слабее пятая гармоника. Степень проявления третьей и пятой гармоник зависит от значения наибольшей индукции, допускаемой в сердечнике трансформатора, а также от сорта железа. В таблице 7 приведены примерные значения амплитуды высших гармоник, выраженные в процентах от амплитуды основной гармоники, при разных значениях наибольшей индукции (же,-лезо - высоколегированное).

ТАБЛИЦА 7.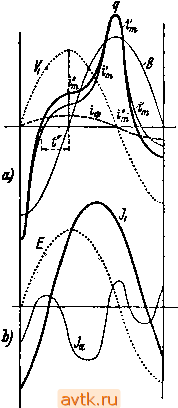

Рис. 68.

Из таблицы 7 видно, что чем больше значение наибольшей индукции в сердечнике, тем эффективнее проявление третьей и пятой

гармоник. Учитывая значительное возрастание третьей гармоники свыше индукции 5шах= 14000, в настоящее время стараются удержать значение наибольшей индукции в сердечниках трансформаторов в пределах 11000-14 000. Из изложенного следует, что

для того, чтобы магнитный поток трансформатора с железом был синусоидальным, намагничивающий ток его должен быть несинусоидальным и содержать главным образом третью и пятую гармоники.

§ 22. Эквивалентный ток холостой работы трансформатора.

Несинусоидальный ток непригоден для изображения его на векторных диаграммах, ибо в них векторами изображаются величины, меняющиеся во времени по закону синуса.

В целях облегчения изучения главнейших явлений в трансформаторе несинусоидальный намагничивающий ток заменяется синусоидальным эквивалентным током, т. е. таким, который доставлял бы трансформатору ту же мощность и создавал бы такой же магнитный поток, что и действительный ток. Найдем этот эквивалентный ток.

Мощность, доставляемая трансформатору, работающему вхолостую, расходуется в нем самом на покрытие потерь в меди первичной обмотки и потерь в железе от гистерезиса и токов Фуко. Первые потери происходят от омического сопротивления первичной обмотки; они ничтожно малы, так как ток холостой работы трансформатора незначителен. Потери на гистерезис происходят от работы, которая затрачивается на преодоление молекулярного трения при перемагничении железа. Эти потери за один период перемагничении железа пропорциональны площади шлейфа гистерезиса (на рис. 67-площади abed); они зависят, следовательно, от величины магнитной индукции в железе трансформатора. Штейн-мец экспериментально установил, что потери на гистерезис железа возрастают пропорционально индукции в степени 1,6. В настоящее время при расчетах часто принимают,.что потери на гистерезис меняются пропорционально индукции во второй степени.

Следуя Арнольду, потери на гистерезис можно определить по следующей формуле, являющейся развитием известной формулы Штейнмеца:

Рг = г

где - постоянная гистерезиса, которую для хороших сортов железа можно принять равной единице, а для железа, содержащего кремний, меньше единицы, а именно 0,5 - 0,63; /-частота переменного тока в герцах; - наибольшее значение индукции в железе в гауссах и Vm.- объем железа в кубических дециметрах.

Потери от токов Фуко происходят от паразитных токов, которые индуктируются переменным магнитным потоком в листах железа трансформатора. Эти токи проходят в поперечном сечении каждого листа по примерным путям, указанным на рис. 69, совпадая по направлению с вторичною электродвижущею силою во вторичной обмотке; они порождаются электродвижущими силами, индуктируемыми в контурах, подобных указанным пунктиром на рис. 69.

Потери от токов Фуко являются джоулевыми потерями в массе железа; они пропорциональны этим токам во второй степени. Но так как порождающие токи Фуко электродвижущие силы пропорциональны потокам, пронизывающим контуры, в которых они образуются, т. е. индукции в железе, а также пропорциональны числу периодов изменения потока, то в общем потери от токов Фуко пропорциональны индукции в железе и числу периодов во второй степени. С достаточной для практики точностью эти потери могут быть

определены по формуле Арнольда: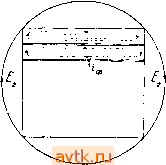

1Ф-ф[а 100-1000/

ж ватт.

где Оф-постоянная, которая для обычных сортов железа находится в пределах от 1,3 до 1,6, для железа же с кремнием- в пределах от 0,4 до 0,5; d - толщина листов железа в миллиметрах.

При плохой сборке сердечника, когда отдельные листы железа соединяются между собою электрически железными заусеницами и изоляция между ними в виде лака или тонкого слоя бумаги как бы аннулируется, потери от токов Фуко могут быть значительно больше вычисленных по приведенной формуле.

Видмар дает следующую формулу для общих потерь в железе от гистерезиса и токов Фуко:

Рис. 69.

10 000

f f \50

где -вес железа в килограммах; ЛГ, - постоянная потерь, которая для высоколегированного трансформаторного железа равна приблизительно 1,3 VJ/кг, а для обычного легированного железа составляет 2,3 W/кг.

При быстрых подсчетах потерь в железе можно воспользоваться кривыми, изображенными на рис. 70, которые дают потери в 1 кг пластинчатого железа толщиною 0,35 и 0,5 мм при разных индукциях и при частоте 50 Hz, Кривые построены по данным таблицы 2.

одая потери от гистерезиса и от токов Фуко в железе трансформатора, легко определить ту активную составляющую эквивалентного синусоидального тока, которая идет на покрытие этих 70

потерь. Обозначив ее через / имеем:

где - первичное напряжение.

Значение потерь в железе трансформаторов по Общесоюзному стандарту (ОСТ -4815) см. в конце книги Приложения .

Найдем теперь реактивную / составляющую эквивалентного тока.

Реактивная составляющая эк- 4 Бивалентного тока / х^ идущая на создание собственно магнит- з ного потока, должна содержать реактивную составляющую /oi первой гармоники тока /, и все токи высших гармоник 1а, ибо эти последние токи, имея иную о периодичность, чем первичное напряжение К„ по отношению к нему являются реактивными.

Таким образом, реактивная составляющая эквивалентного синусоидального тока будет

т 4т воос sm ,то пт шоо mi Z в усо ы

Рис. 70.

Реактивную составляющую тока /o.v, или собственно намагничивающий ток, т. е. ток, создающий собственно магнитный поток,

можно определить, зная величину магнитного потока и размеры магнитной цепи.

Пусть, например, - наибольшее значение магнитного потока,. Qc и Ря -поперечные сечения стержня и ярма сердечника в квадратных сантиметрах, 1с и 1я - средние длины путей магнитного потока в стержне и в ярме в сантиметрах (рис. 71). Тогда индукция в обоих стержнях стержневого трансформатора и в среднем стержне броневого трансформатора будет равна

Ф

индукция в ярме стержневого трансформатора

Ф

5я=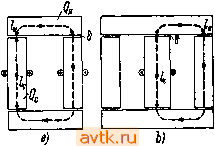

Рис. 71.

индукция в ярме и боковых стержнях броневого трансформатора

полнощека

(в предположении, что сечения ярма и боковых стержней одинаковы).

Зная кривую намагничения для данного сорта железа (рис. 72), находим ампервитки на сантиметр при определенных значениях индукции: при В„ awn при Вя, а-ноя при B . (Нижний

масштаб для ампервитков соответствует верхней кривой.) Затем находим ампервитки для всего пути магнитного потока по формулам:

при стержневом трансформаторе (рис. 71а)

AW = Ifiw, + 24aw -f 0,8 48 В,;

при броневом трансформаторе (рис. 71Ь)

AW = l,aw, + (24 + Q aw; + 0,8 28 В, + 0,8 28 В,\

В этих формулах под 8 подразумевается длина воздушной щели, которая получается в месте стыка между ярмом и сердечником; приближенно можно считать 8=0,005 сж; у трансформаторов большой мощности 8 = 0,05-0,15 см.

Если мы поделим найденные намагничивающие ампервитки на число витков первичной обмотки w то получим наибольшее значение намагничивающего тока /одтах. Действующее значение намагничивающего тока

J Dx шах

20С00

кто

S0O0

гоо Рис. 72.

т

Следует заметить, что соотношение между наибольшими действующим значениями намагничивающего тока, равное i/2= 1,41, предполагает синусоидальное изменение этого тока. В действительности намагничивающий ток, как показывает кривая рис. 68а, меняется по заостренной сверху кривой. Вследствие этого отношение между наибольшим и действующим значениями действительного намагничивающего тока больше \/2. При индукциях 11000- 14000 это отношение находится в пределах 1,6-2,3.

Имея активную и реактивную составляющие эквивалентного синусоидального тока, легко найти и самый ток, используя для этой цели диаграмму рис. 73. На этой диаграмме вектор Оа изображает магнитный поток Ф^, вектор Ое изображает приложенное к первичной обмотке напряжение V опережающее поток на 90°; вектор Ob изображает реактивную составляющую эквивалентного тока /од:, совпадающего по фазе с магнитным потоком; вектор Од.

изображает активную составляющую эквивалентного тока hr, совпадающего по фазе с напряжением V,. Равнодействующий вектор Ос дает полный эквивалентный ток / . По величине он определится выражением

По фазе эквивалентный ток опережает магнитный поток на угол а.

Пример. Определить ток холостой работы трансформатора с первичным напряжением 1, = 120 V, у которого число витков первичной обмотки w, = 45, поперечное сечение железа сердечника (стержней и ярма) Cl,= 100 cjи^ средняя длина магнитного потока 4 = 110 см, частота/=50 Hz.

Решение. Пользуясь выражением для электродвижущей силы

£,=4,44/w, Ф„- ЮЛ

определяем магнитный поток

= 1.2.10е.

Щ-50 45-10-Индукция в сердечнике

Ф„, 1,2 10

= 12 000.

Qc ~ 100

По кривой намагничения, рис. 72, при индукции В= 12000 необходимые ампервитки на сантиметр равны aw = 8. Следовательно, полное число намагничивающих ампервитков будет

AW=aw-l, = 110 = 880.

Наибольшее тока

значение намагничивающего

>ox

4л шах-

= 18,6 А.

Рис. 73.

Действующее значение намагничивающего тока

hx =

£ = 13,6

Объем железа сердечника г'. ;=110- 100 см. Считая удельный вес железа равным 7,5, получаем вес сердечника равным 82,5 нг. По кривым рис. 70 находим потери на 1 кг при индукции В = = 12 000 равными 2 W. Следовательно, общие потери будут равны 282,5= 165 W. Активная составляющая тока холостой работы

/ =1 = 14 120

Ток холостой работы

4= Kl,4* + 13,6 = 13.7 А.

Определенный таким образом намагничивающий ток / практически весьма мало отличается от того тока, который в действительности идет в первичной обмотке трансформатора при холостой его работе. Поэтому ток / и называют током холостой работы трансформатора.

Так как трансформаторам часто приходится работать вхолостую, то при изготовлении их стараются по возможности снизить мощность и ток холостой работы. Первое, как уже было указано, достигается применением железа с меньшими потерями в нем, лучшей изоляцией листов, а второе достигается допущением меньшей индукции в железе (в пределах 10000-14000) и лучшей сборкой сердечников.

В таблице 8 даны в процентах от нормального тока наибольшие значения тока холостой работы, установленные, как предельные. Французским электротехническим комитетом для трансформаторов разных типов.

ТАБЛИЦА 8.

Токи ХОЛОСТОЙ работы в процентах от нормального тока.

Трансформаторы однофазные lOkVA или трехфазные 15 kVA:

1) масляные с пониженными потерями (осветительные).........

2) масляные с нормальными потерями (силовые)..............

3) сухие................

Трехфазные трансформаторы свыше

250 kVA, масляные с естественным охлаждением:

1) с пониженными потерями . . . .

2) с нормальными потерями.....

10,5

20 15

4,4 9,5

23,5 19

4,9 10,1

16 29

5,1 11,5

16,5 11,8

3,5 7,6

19,5 15,4

4,0 8,2

13 23

4,3 9.3

Как видно из таблицы 8, процентное значение тока холостой работы уменьшается с увеличением мощности трансформатора. У осветительных трансформаторов, работающих вхолостую и рассчитываемых обычно с пониженными потерями, т. е. с небольшой индукцией в железе, процентное значение тока холостой работы меньше, чем у силовых трансформаторов, редко работающих вхолостую. Наконец, у трансформаторов высокого напряжения, у которых длина сердечника получается несколько большей, чем у трансформаторов низкого напряжения (в целях рациональной конструкции обмотки), процентное значение тока холостой работы; больше, чем у трансформаторов низкого напряжения.

§ 23. Вопросы для самопроверки.

1. Каково выражение для электродвижущей силы трансформатора?

2. Как влияет насыщение железа на форму кривой намагничивающего тока?

3. Как влияет гистерезис на форму кривой намагничивающего

4. Какие гармоники содержит кривая намагничивающего тока?

5. Как определяется эквивалентный ток холостой работы трансформатора?

6. Магнитная цепь трансформатора 1000 kVA имеет среднюю длину 240 см и среднее сечение сердечника 1800 cм'. Этот трансформатор рассчитан для работы при напряжении 66 ООО V и при частоте 50 Hz. Сколько витков должна иметь обмотка, если наибольшая индукция равна 10800 гауссов? Каковы ток и коэфициент мощности (cos tpj холостой работы трансформатора?

ГЛАВА ШЕСТАЯ.

ЯВЛЕНИЯ В ТРАНСФОРМАТОРЕ ПРИ НАГРУЗКЕ.

§ 24. Магнитодвижущие силы обмоток трансформатора

при нагрузке.

При холостой работе трансформатора в его магнитной цепи действует магнитодвижущая сила тока одной первичной обмотки.

Как только мы нагрузим трансформатор, в магнитной цепи его будет действовать магнитодвижущая сила вторичной обмотки, равная 0,4it/, 1/22, где Д - ток во вторичной обмотке, а - число витков этой обмотки. Согласно закону Ленца магнитодвижущая сила вторичной обмотки действует против магнитодвижущей силы первичной обмотки. Вследствие этого магнитный поток трансформатора несколько уменьшится. Но магнитный поток, не может уменьшиться в значительной степени: его поддержит приложенное к первичной обмотке постоянное напряжение. В самом деле, с уменьшением магнитного потока уменьшится несколько первичная электродвижущая сила, уравновешивающая приложенное к первичной обмотке напряжение. Вследствие этого в первичную обмотку пойдет больший ток и настолько больший, что магнитодвижущая сила первичной обмотки скомпенсирует размагничивающее действие вторичной магнитодвижущей силы и одновременно создаст магнит: ный поток, почти равный магнитному потоку при холостой работе.

Изложенное взаимодействие магнитодвижущих сил обмоток трансформатора весьма наглядно иллюстрируется векторной диаграммой, изображенной на рис. 74.

На рис. 74 дано сложение не магнитодвижущих сил первичной и вторичной обмоток, а ампервитков их, которым они пропорциональны, т. е. векторами изображены произведения Дда, и Iw, где , и 4 - токи, а и - числа витков первичной и вторичНой

обмоток. Диаграмма начерчена в предположении, что вторичный ток 4 отстает от вторичной электродвижущей силы на угол

На диаграмме рис. 74 вектор Оа изображает магнитный поток Ф„; вектор Ос, изображает вторичную электродвижущую силу f смещенную относительно потока Ф на 90° в сторону отставания; вектор Od изображает ампервитки вторичной обмотки Iw, совпадающие по фазе с йториЧнйм током /,; вектор Ое изображает айпервитки первичной обмотки совпадающие по фазе с пер-

йичным током Д.

Как видно из диаграммы, ампервитки первичной обмотки можно рассматривать как состоящие из двух составляющих. Одна составляющая, изображенная на диаграмме вектором Of, равна и противоположна ампервиткам вторичной обмотки. Эта составляющая компенсирует размагничивающее действие вторичной обмотки. Вторая составляющая, изображенная на диаграмме вектором Ob, совпадает по фазе с магнитным потоком. Эта составляющая создает магнитный поток при нагрузке. По величине последняя составляющая почти равна ампервиткам первичной, обмотки при холостой работе, т. е. / да,.

Таким образом можно сказать, что и при нагрузке трансформатора магнитный поток создается собственно первичною обмоткою-Но так как первичная обмотка создает фактически ампервитки а не составляющие их, то можно сказать и так, что магнитный поток создается равнодействующей из ампервитков первичной и вторичной обмоток, которая получается геометрическим сложением их. На рис. 74 эта равнодействующая магнитодвижущая сила изображена вектором Ob.

Если пренебречь составляющей Ob, как весьма небольшой в сравнении с составляющей Of, то можно сказать, что Oe = Od, или 7,1 = /jW,; но Wi:Wi = Ei:E. Следовательно,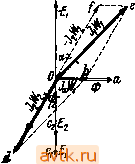

Рис. 74.

£ ,4 - Е^1,

мощность первичной обмотки, выраженная в вольт-амперах, равна мощности вторичной обмотки, также выраженной в вольт-амперах.

Это последнее равенство непосредственно следует из закона сохранения энергии. Если пренебречь потерями в обмотках и железе, то можно сказать, что вся мощность, получаемая первичною обмоткою трансформатора от сети, передается вторичной обмотке его, причем передатчиком является магнитный поток.

§ 25. Поток рассеяния и вы:)ываемое им реактивное сопротивление обмотки трансформатора, работающего

вхолостую.

Разбирая принцип действия трансформатора, мы видели, что магнитная связь между первичною и вторичною обмотками несовершенна: не весь магнитный поток первичной обмотки сцепляется со всеми витками первичной и вторичной обмоток. Имеются силовые линии потока, которые сцепляются лишь с частью витков первичной обмотки и совершенно не сцепляются с витками вторичной обмотки. На рис. 75а изображены примерные пути прохождения силовых линий магнитного поля, создаваемого одною лишь первичною цилиндрической обмоткою. На этом рисунке буквою Ф обозначен главный магнитный поток, проходящий через сердечник трансфор- матора и сцепляющийся со всеми витками первичной и вторичной обмоток. Буквою же Ф^ обозначена часть силовых линий поля первичной катушки, которые совершенно не сцепляются с витками вторичной и потому являются силовыми линиями магнитной утечки или магнитного рассеяния. Но если силовые линии поля рассеяния совершенно не сцепляются с витками вторичной обмотки и потому в ней не индуктируют электродвижущей силы, то с витками первичной обмотки эти силовые линии сцепляются, хотя и в разной степени. Например, силовая линия 1 на рис. 75а сцепляется с небольшим числом витков первичной обмотки; силовая линия 2 сцепляется с бдльшим числом витков; силовая линия 3 сцепляет .я с еще ббльшим числом витков обмотки и т. д. Так как поле рассеяния есть поле переменное во времени, то оно индуктирует в витках обмотки электродвижущую силу, которую мы можем определить по общей, ранее выведенной формуле, а именно

Рис. 75.

л

В этом выражении Фд.ге/д. заменят произведение Фт® которое

имелось в формуле для первичной электродвижущей силы и кото-

рое было равно числу .потокосцеплений главного потока Ф„ со всеми витками обмотки, х'д: есть сумма потокосвязей поля

рассеяния с витками первичной обмотки. Эту сумму можно представить в следующем виде:

Ф^Ы>х = Ф' w + Ф w + Ф' w

где Ф' - число силовых линий сцепляющихся с w витками, Ф ~ число силовых линий сцепляющихся с w витками, и т. д.

Если через Ф^, обозначить фиктивный поток рассеяния, который, предположим, сцепляется со всеми витками первичной обмотки, индуктируя ту же электродвижущую силу Е^, и для которого существует равенство

л

то мы можем написать

si = yjfwi Ф,. 10- .

л

Тогда можно написать

Число потокосцеплений магнитного поля с обмоткою при токе в ней силою 1 А называют коэфициентом самоиндукции. В рассматриваемом случае Lt - коэфициент самоиндукции первичной обмотки, отвечающий полю рассеяния ее.

Выражение для электродвижущей силы поля рассеяния первичной обмотки при токе холостой работы / можно написать и так:

здесь х, = 2i:/I, есть реактивное сопротивление первичной обмотки, вызываемое ее полем рассеяния; произведение /,а:, - падение напряжения в реактивном сопротивлении первичной обмотки (подобно тому как произведения I Ri - падение напряжения в активном сопротивлении первичной обмотки ?,). 78

Величина реактивного сопротивления обмотки зависит от типа обмотки и от расположения ее отдельных катушек на сердечнике трансформатора. Но для данного трансформатора и для данной частоты тока реактивное сопротивление считается величиной постоянной и не зависящей от тока.

Падение напряжения от реактивного сопротивления обмотки учитывается в векторной диаграмме вектором, смещенным относительно вектора тока этой обмотки на 90° в сторону запаздывания.

§ 26. Потоки рассеяния и вызываемые ими реактивные сопротивления обмоток трансформатора, работающего под

нагрузкой.

При работе трансформатора под нагрузкою токи имеются как в первичной, так и во вторичной обмотках, причем эти токи имеют почти взаимно противоположные направления. В этом случае обе обмотки создают вокруг себя поля рассеяния, сцепляющиеся только со своими обмотками.

На рис. 75Ь показана примерная картина njrreft прохождения силовых линий полей рассеяния при наличии токов в первичной и вторичной обмотках с цилиндрическими катушками. Предположено, что в первичной обмотке ток направлен от зрителя, тогда как во вторичной обмотке ток направлен к зрителю. Нетрудно видеть, что группы проводников первичной обмотки 1 и вторичной П образуют как бы соленоид со щелью А между ними. .В этой щели проходят силовые линии полей рассеяния обеих обмоток, а потому индукция поля рассеяния в щели имеет наибольшее Значение. В точках левее или правее щели А индукция будет иметь уже меньшее значение, так как силовые линии рассеяния, например 1 или 2, создаются меньшим числом ампервитков. ПОииерное распределение индукции по линии р, перпендикулярной к оси катушек и проведенной в середине их, можно изобразить ломаною кривою abed.

На рис. 76 изображено примерное распределение силовых линий полей рассеяния трансформатора с тремя цилиндрическими катушками, из которых крайние катушки (наружная и внутренняя) принадлежат вторичной обмотке, а внутренняя катушка принадлежит первичной обмотке. Предположив, что токи в первичных и вторичных катушках идут во взаимно противоположных направлениях, легко усмотреть, что ломаная кривая abcdef дает распределение индукции по ширине катушек и по ширине щелей между ними.

На рис. 77 представлена примерная картина распределения силовых линий поля рассеяния в трансформаторе с дисковыми обмотками, в предположении, что катушки первичной и вторичной обмоток чередуются друг с другом. Предположив, что токи в первичных катушках (заштрихованных в одну сторону) и во вторичных катушках (заштрихованных в другую сторону) имеют взаимно противоположные направления, легко видеть, что ломаная кривая abcdef изобразит распределение индукции поперек катушек (по линии параллельной оси сердечника) и поперек щелей между ними. Магнитные силовые линии полей рассеяния, как видно из рис1 76

и 77, проходят главным образом через воздух и потому на них не оказывает влияния задерживающая сила железа сердечника. Это значит, что магнитные поля рассеяния можно считать совпадающими по фазе с токами, их создавшими.

Магнитные поля рассеяния, будучи переменными во времени, индуктируют в обмотках электродвижущей силы

где и - коэфициенты самоиндукции первичной и вторичной обмоток, отвечающих их полям рассеяния; /j и 4 - токи в обмотках.

Обозначив через и произведения 2ir/Ii и 2i:fL и назвав их реактивным сопротивлениями первичной и вторичной обмо-

ток, получим:

Произведения Xyli и х,/, называются падениями напряжения от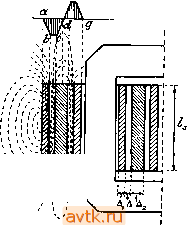

iSiV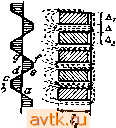

Рис. 76.

Рис. 77.

реактивных сопротивлений первичной и вторичной обмоток.В векторных диаграммах эти падения учитываются векторами, смещенными относительно соответствующих токов на 90° в сторону запаздывания.

Следует заметить, что пути прохождения магнитных линий потоков рассеяния не остаются постоянными, а меняются в течение каждого периода изменения тока. Чтобы уяснить себе по существу весьма сложное явление рассеяния магнитного потока в трансформаторах при нагрузке, рассмотрим сложение магнитодвижущих сил первичной и вторичной обмоток в разные моменты времени за один период изменения тока.

На рис. 78 изображены кривые изменения во времени магнитодвижущих сил: первичной обмотки - кривая ABC и вторичной обмотки- кривая DEF. Обе кривые взаимно сдвинуты на угол 180°-а, соответственно диаграмме рис. 74. Изменение равнодействующей магнитодвижущей силы, создающей потоки за целый период, представится при 9Т0М кривой MNP, Как видим, в 1-й момент времени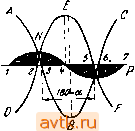

Рис. 78.

магнитодвижущие силы обеих обмоток равны и прямо противоположны; равнодействующая магнитодвижущая сила равна нулю, следовательно главный поток, сцепляющийся с обеими обмотками I к II (рис. 79), на котором изображена лишь одна половина броневого трансформатора, также равен нулю. Потоки же рассеяния образуются как первич-ною обмоткою, так и вторичною обмоткою, причем пути замыкания их будут соответствовать рис. 79. В период времени от 1-го момента до 2-го (см. рис. 78) магнитодвижущая сила первичной обмотки преобладает над магнитодвижущей силой вторичной; главный потрк создается исключительно первичной обмоткой. Поток рассеяния замыкается

только вокруг первичной обмотки, причем этот поток составляется из двух потоков: потока, создаваемого непосредственно первичным током (на рис. 80 потока Ф^)), и потока, который замыкается во-

[ круг первичной обмотки под действием

вторичной магнитодвижущей силы, противоположной по действию первичной магнитодвижущей силе и как бы отталкивающей магнитные линии главного потока к первичной обмотке (на рис. 80 потока Ф^а). Этот последний поток, хотя и замыкается вокруг первичной обмотки, обязан, однако, своим существованием вторичной обмотке. Потока рассеяния, замыкающегося вокруг вторичной обмотки, например, по линии АВ, быть не может, так как в пространстве между катушками I и II не могут существовать одновременно потоки разных направлений. Итак, в период времени от 1-го до 2-го момента (рис. 78) потока рассеяния вокруг вторичной обмотки не имеется, поток же рассеяния вокруг первичной обмотки усиливается вследствие размагничивающего действия вторичной обмотки. Во 2-й момент

имеется только одно первичное рассеяние, I

так как вторичный ток равен нулю. В период времени от 2-го до 3-го момента первичный и вторичный токи совпадают по направлению и потоки рассеяния замыкаются вокруг обеих обмоток, так как будто они составляют одну обмотку. В 3-й момент первичный ток равен нулю, и главный поток создается исключительно вторичным током. В этот момент поток рассеяния замыкается только вокруг вторичной обмотки, т. е. имеется одно только вторичное рассеяние. За промежуток времени от 3-го до 4-го момента вокруг первичной обмотки потока рассеяния не имеется,

Рис. 79.

1 1!

Рас. 80.

но вследствие размагничивающего действия этой обмотки на вторичную, поток рассеяния вокруг вторичной обмотки возрастает. За период времени от 4-го до 7-го момента явление в отоншении вторичной обмотки протекает совершенно так же, как и за период времени от 1-го до 4-го момента в отношении первичной обмотки. Таким образом пути прохождения потоков рассеяния, а также распределение их вокруг обмоток за один период изменения тока непрерывно меняются. Во всяком случае, однако, собственно первичное, как и собственно вторичное рассеяние имеют ту же периодичность изменения, что и главный поток.

При рассмотрении явлений в трансформаторах влияние потоков рассеяния на напряжение учитывается двояко: 1) складывают потоки рассеяния с главным потоком и по равнодействующему потоку определяют электродвижущую силу, уравновешиваю.щую напряжение и падение в активном сопротивлении; 2) определяют электродвижущие силы, которые индуктируются потоками рассеяния в обмотках, и складывают их затем с электродвижущими силами главного потока (Арнольд, Штейнмец). И в том и в другом случае имеют дело до известной степени с фиктивными величинами. Так, в первом случае потоки рассеяния первичной и вторичной обмоток, складываемые с главным потоком, представляют фиктивные величины, ибо в то время как главный поток пронизывает все витки обмотки в одинаковой степени, действительные потоки рассеяния пронизывают только части обмоток, и притом а разной степени. Потоки рассеяния - первичный Ф и вторичный Ф^ - рассматриваются как воображаемые потоки, которые, пронизывая все витки обмотки, как указано на рис. 79, дают такой же эффект, как и действительные потоки рассеяния. Во втором случае электродвижущие силы главного потока и потока рассеяния являются фиктивными электродвижущими силами, ибо в действительности имеется всего одна электродвижущая сила, которая индуктируется всеми линиями магнитного потока, пронизывающими обмотку. Таким об--разом электродвижущие силы главного потока и потока рассеяния представляют собою воображаемые составляющие действительной электродвижущей силы, введенные для облегчения рассмотрения явлений.

Что касается характера распределения потоков рассеяния вокруг обмоток, то он, как мы видели, меняется за один период изменения тока. Однако при определении коэфициентов самоиндукции потоков рассеяния предполагают, что картина распределения потоков рассеяния вокруг обмоток сохраняется неизменной и отвечает той, которая получалась бы в предположении, что токи в обмотках прямо противоположны.

В качестве примера определим коэфициенты самоиндукции от полей рассеяния цилиндрических катушек трансформатора. Разобьем силовые линии поля рассеяния каждой катушки на две группы: на группу линий, проходящих через щель А и сцепляющихся со всеми витками катушки (на рис. 75Ь силовые линии 4-4) и на группу линий, проходящих через толщу катушки и сцепляющихся с частью витков этой катушки. Так как силовые линии поля рассеяния внутренней катушки I замыкаются .через железный сердеч-

82 тт,

ииЬлиот^ка

ник с весьма малУм магнитным сопротивлением, то мы мои^ем ё качестве магнитного сопротивления для этих силовых линий считать только сопротивление пути в воздухе по высоте катушки 4-То же сопротивление мы будем принимать и для силовых линий поля рассеяния наружной катушки II, ибо вне катушки силовые линии замыкаются в беспредельном пространстве воздуха и, следовательно, встречают незначительное сопротивление.

Обозначим ширину первичной и вторичной катушек через и Д^, ширину щели Л между катушками через Д, среднюю длину окружности первичной и вторичной катушек через 1 и щ, среднюю длину окружности щели А через

Предполагая, что одну половину щели занимает группа силовых линий первичной катушки и другую половину щели занимает группа силовых линий вторичной катушки, найдем сопротивление для каждой группы

Так как силовые линии щели создаются всеми ампервитками катушки, то магнитный поток катушки, например первичной, проходящий только через щель, будет

д. 0,4тс / да, 0,4:: г ТО,

27Г

а число потокосвязей будет

0,4л iw Ды

= ---0-/---

Для того чтобы определить число потокосвязей второй группы силовых линий, проходящих через толщу сечения катушки, поступим следующим образом. На расстоянии х от края катушки (см. правую сторону рис. 7оЬ) выделим силовую трубку шириною dx и длиною по окружности катушки и„. Ее сопротивление будет

~гг-, где н, -средняя длина окружности катушки, принятой ах и„

одинаковой для всех трубок шириною dx.

Выделенная нами трубка создается ампервитками f-~ а;, ибо число витков катушки от внутреннего края катушки до конца длины х будет -~ X. Таким образом поток трубки равен

0Лт:1-Х ... ,

ф^ .1 OA-iw-x dx-u

dx-u