; Из анализа этих коэффициентов чувствительности видио, что при допусках на па;раметры элементов, равных 1%, разброс аначеиий частоты too *и добротности Q составит соответсивенно 1 0,77о-

Пример 2. Необходимо рассчитать активный ФВЧ второго порядка с максимально плоской характеристикой, коэффициентом усиления Ао=-20 в полосе пропускания .и ав-=0,5 дБ ,на частоте /в-=1 кГц.

Пользуясь той же таследо1вателвностью расчета, что и ib предыдущем случае, получим too=2jt-591 c~ я Q = 0,7071il.

-Поокольку коэффщиент усиления сравнительно большой, то применим базовую схему, П'риведениую в табл. 7.15. Приме1Няя преобразование CR, R-C и выбирая =5 (кОм, получаем: Ri=4RiQ(\l+\Ao])=ZlO кОм; Ci = = ИоС2/(1 + Ло )=36,28 иФ; ~ C2=l/2Qtoo/?i =38,09 нФ; Сз=С2/(1+Ио) = = 1,814 нФ. . - .

Рассчитанная таким образом (схема показана иа рис. 7.9й. Используя значения параметров фильтра, приведенных в табл. 7.il.5, коэффициенты чувствительности можно представить ,в следующем (ВЙде:

s:= s?-=

Ci 1

(HoR С^Сз 2,1

Q (Ci , Л J , 2

Q (Ci Л I

- too Ri Сз

54°= - s;S = i.

Из этих ..выражений следует, что при допустимом разбросе Параметров элементов ib пределах 1 % ПреДвл отклонения частоты too и добротностл .Q также , равен 17о.

В связи с тем, что хара.ктеристики ОУ Являются частотно-зав'исимыми, расчетные и фактические характеристики не будут полностью совпадать. Расхождение вблизи частоты \и = \ кГц можно определить из соотношения (7.25). Однако для этого Необходимо знать частотную характеристику коэффициента обратной связи

P(s)

i[l±lQ!a + Moi)L ,

Подставляя значения из дагнного примера, можно поСтроитъ частотную характеристику l/P(jfi)) , приведениую на рис. 7.96. .Из этой характеристики видно, что значение l/P(jtu) равво единице яа нулевой частоте, 1 + Ио =21 на частотах, зна'чителвно превышающих tOo, и 29,2 на частоте 0,88й)й. Вблизи максимального значения, равного 29,2, коэффициент усиления шетли примерно . равен 50 дБ. П.оэто1му в наихудшем - .в смысле значения фт - случае погрешность амплитудной характеристики не будет превышать 0,3% (в наихудшем случае фг равен О .или 1180°). На высоких частотах к указанной погрешности будет доба.вляться погрещность коэффициента усиления- [см. выражение (6.50)].

Пример 3. Требуется рассчитать эллиптический фильтр с единичным коэффициентом усиления, 7н=-1 кГц, ан=0,5 дБ, fs=2 кГц, as>40 дБ.

Из табл. 7.9 видно, что эту задачу можно решить поС,редствО'м использования эллиптического фильтра четвертОГо порядка, им.еющего (следующие относи-

тельные значения параметров: (Ooi= 1,04181, Qi=.2,97359, tao2=0,72862, Cuz= =2,02109, Q2=0,61279.

В результате использования базовых схем, приведенных в табл. 7.13 и 7.22, для реализации ФНЧ .второго по-рядка и эллиптического фильтра получена схема, приведенная на рис. 7.10.

Рис. 7.10

При помощи выражений (7.29)-(7.31) определены параметры -настройки ФНЧ: f,n=.l,012 .кГц, lA(jcu)max=S,016 (9,59 дБ), fc=.l,586 кГц. Пиковое значение А (jto) I max можно установить путем изменения опношения С1/С2 при поддержании постоянным произведения С1С2. Частоту fm можно регулировать с помощью резисторов R\=R2=R.

В эллиптическом фильтре частоту, ооотВетст1вующую яулю, f2=2,021 Гц и добротность Q можно регулировать .соответственно с .помощью резисторов Rfs

и R7.

Хотя выбор значения Q2 можно проконтролировать посредством измерения коэффициента ослабления на квадратурной частоте [ш .выраж-ення (7.32) A(jtoo) 900=0,533, т. е. -5,46 дБ]., все же лучше это .сделать ib соответствии с суммарной характеристикой обеих базовых .схем.

Пример 4. Необходимо рассчитать полосовой фильтр, имеющий н1 = =800 Гц, fb-2-1200 Гц, ая<\ Ф, fsi=400 Гц, /82=1600 Гц и as>40 дБ.

Используя преобразование в соответствии с выражением (7..1.1), получим £2н = 1, ан = 1 дБ, fis = 2,500, as>40 дБ.

Этим требованиям удовлетворяет эллиптический фильтр третьего порядка. Из -табл. 7.8 имеем 2о=£2е= =0,52312, 2i=0,22767, fii=0,97638, fi2=fi=2,78505 (.см. рис. 7.11,а). Частотную ха,ра1ктер-нстику .с такими параметрами можно реализовать, иопсльэуя один полосовой фильтр второго .порядка и два эллиптических филь11р,а второго по-ряд-ка. Воопользуемоя схемами, приведенными в табл. 7.17 и 7.23, со следующими -начальными -дан- -ными (рис. 7.11,6): (Оо1= ]/0 + +(01=6156,26 с-1, cuo2=1/ 0Vf +(022=5049,36 .c-i, (003=1/03+ +(о2з=7505,89 Qi=tooi/20i=

=4,68, Q2=coo2/202= 10,97, Qi= =сооз/20з= 10,97, С0й=с04=3581,73 с-, шгз=м5=1058,1,51 с-.

Полная схема -фильтра показана иа рис. 7.12.

Рис. 7.11

ГЛАВА 8

ИНТЕГРАЛЬНЫЕ АНАЛОГОВЫЕ ПЕРЕМНОЖИТЕЛИ

8.1. Аналоговые перемножители

Аналоговый перемножитель является активным устройством, выходное напряжение которого пропорционально произведению двух входных. С использованием обозначений на рис. 8.1 выполняемую им функцию можно записать

Uz==KUxUy, (8.1)

где/С - масштабный коэффициент. . . ,

Рис. в.1. Аиаломвый реремножитель: а - Ю'боэиатенис; б - эквивалеитя схама

От адасштабного коэффициента зависит единичное напряжение, при котором UxiVyi = Uzi.

Цдеальный перем1Ножитель имеет бесконечные полные входные сопротивления, нулевое выходное сопротивление и частотно-независимый масштабный коэффициент, который не зависит ни от f-jc, ни от С/у. Его выходное напряжение равно нулю, когда хотя бы одно из входных напряжений равно нулю. Другими словами, напряжения смещения, дрейфа и шума равны нулю.

Реальные перемножители являются только приближениями идеального уст1ройства и имеют конечные напряжения смещения, дрейфа и шума. Для того чтобы вызываемые ими погрешности

имели приемлемый уровень, единичные напряжения должны выбираться довольно большими, обычно от 1 до 10 В.

Из множества известных спосюбав построения интег1ральных аналоговых устрюйств умножения наиболее пригодными являются следующие.

Логарифмическое суммирование (рис: 8.2). Реализация этого метода основана на использовании следующего соотношения:

Z=Xr=exp(logX-l-logy). Uz = ехр (log Ux + log ky Uy .

(8.2)

tog. l

апШод

const

Рис. 8.3. Амплипудио- и ши-р 0та1о-1ИМ1пульсн а я мшу ляция

Рис. 8.2. Люгарифмическре чуммироваиие

Ам п л и т у д н о - и м и у л ыс и а я и ш и р € т н о - и м п у л ь с -ная модуляция (рис. 8.3). Этот М'Стод базируется на том, что, если X=kxA, Y==kyt и Z=kiT, где А - амплитуда импульса; / - его длительность; Г--площадь импульса, то Z-{kzlkJiy)XY, поскольку

T = At. (8.3)

Управляемое распределение тока (рис. 8.4). Суть этоло Метода заключается в том, что выходной диффе|ренциаль-ный ток управляемого линейного делителя тока пропорционален произведению. Из рис. 8.4 следует, что выходные токи и их разность соответственно равны

/i = л: / ,/,=(1 -X) / , /1-/2 = (2 л;-1) /о-

(8.4)

X = kAx-\),Y = kyI

0>

(8.5) (8.6)

Рис. 8.4. Управляемое

раагфсделение тока

2 = ,(1-/2) =г/2.

Z = {kJkky)XY.

Основной недостаток первого метода заключается в том, что напряжения Ux и Uy должны быть положительными и не могут уменьшаться до нуля (см. § 6.10). Второй метод обеспечивает вы-

сокую точность, но неприподен для .применения на высоких частотах вследствие ограничений, обусловленных невысокой скоростью переключения. Улравляемые делители тока хороШ'О работают и на высоких частотах. Более того, их легко реализовать на осиове функциональных узлов, описанньгх в гл. 4.

8.2. Умножение при помощи управляемых напряжением делителей тока

Простейший .способ реализации управляемого напряжением делителя тока заключается в использовании си1Мметрич1Ного дифференциального каскада, коллекторйые токи которого определяются выражениями (4.28) и (4.29). Пусть Ux обозначает напряжение Ubkx-С/вх2* которое пропорционально параметру X, а /у - ток /о, который пропорционален параметру У (см. рис. 8..5). Считая,

п .

Rx Ru

Ifl1-x)Iff(1-x}rY

= Ux I

Рис. 8.6. У1п|ра1вляе.мый напряжением (делитель (тюка на (основе (симмеяричиюго дифференциального (каскада

ЧТО коэффициенты усиления по току велики, т. е. а~1, показанный на рис. 8.5 парамет|р х (можно записать

X = Illy = 0,5 [ 1 + th {Vx 12 )], (8.7)

откуда -

(2 х- 1) = (I-Q/Iy = th {Ux /2 Ut). (8.8)

До тех пор пока Ux будет значительно меньше 2Ut, {2х-1) Ux/2Ut.

Для дифференциальных составляющих выходного тока и напряжения, которые пропорциональны параметру Z, можно записать следующие соотношения:

Ix-h==hlYUxl2UT; .- (8.9)

. Uz=-R,Iz7-{.RkIUi)IyUx. (8.10)

Рис. 8.6

Из этих выражений видно, что параметр Z пропорционален XY.

При использовании схемы н а рис. 8.5 необходимо найти компромисс между просто-, той и следующими ограничениями: а) поскольку /о=/у не может быть отрицательным, данная схема является двухквадрант-ным перемножителем (рис. 8.6); б) перемножитель является линейным по каналу Iy, но нелинейным по каналу Ux вследствие нелинейности характеристики усилителя, поэтому Ux не должно превышать нескольких милливольт; в) масштабный коэффициент К==-Нк/2ит=-дЯк/2кТ, зависит от абсолютной температуры Т.

Первый недостаток можно устранить посредством применения четырехивадрантной схемы (рис. 8.7), в оторый П)рименяются три управляемых напряжением делителя тока. Используя обозначения на QTOiM рисунке, получаем

Iz=h-h==yxIo+{l-y){l-x)Io-

-y{l-x)Io = Io{2x-l){2y-l), (8.11).

Iz=Ii-h = IoiiUx/2UT)thiUYj2UT), (8.12)

(8.13),

Uz = -RIz = -Rk hth.(f/x /2 Ui) th{UyI2Ut).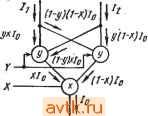

Рис. 8.7. 4©гы1ре мвадра1нггный лерамиожитель а юанше (Ди!ффея>ен.ц:иалыюго

аокада

Полагая, что Ux и Uy знач!ительно меньше 2Ut, благодаря чему гиперболическая функция может быть аппроксимирована линейной, получим

IzfhUxUYlUS и

Uz-RkIoUxUy/Ut

(8.14)

iB этом выражении и Ux, и f/y могут принимать как положительные, так и отрицательные значения. Схема имеет два недостатка. Первый заключается в том, что масштабный коэффициент является квадратичной фуйкцией температуры Т: К=-R}fiIoliUt=-- -qRihlAKT. Второй состоит в том, что гпперболическая функция, оаязывающая токи и на:пряжения, обусловливает нелинейность характеристики по обоим входным сигналам. (Следует отметить, что при работе в составе переключающего перемножителя, когда дифференциальные каскады исиользуются в качестве ограничителей, их гиперболическая характеристика является скорее преимуществом, чем недостатком.) При малых значениях Ux Si Uy нелинейность можно оценить с помощью второго члена разложения в ряд гиперболической функции. Переписывая выражение (8.14) с учетом этого члена, получим:

Uz- (R /0/4 f/V) [ 1 - (Ux + f/V)/12 f/r ] Ux Uy , откуда можно найти относительную пофешность

hx-{Ux +и\)П2и'т- (8.15)

Нелинейности является существенным ограничением в случае работы в режиме усиления сигналов постоянного тока. Например, пусть допустимая погрешность нелинейности будет равна 1 %.

Тогда-значение Kt/-r+f/y не должно превышать 9 мВ, т.е. напряжения, сравнимого с напряжениями смещения и дрейфа. ,

8.3. Умножение при помощи управляемых током делителей тока

Простейший способ реализации управляемого током делителя тока иллюстрируется рис. 8.8, где два токовых зеркала объединены в симметричный дифференциальный каскад. Если транзисторы Ti-Ti имеют значительное усиление (а~1) и пренебрежимо ма-

Рис. 8.8. Управляемый тоном делитель тока .на основе симметр'ичного диффе-

ренцинльвопо каскаиа

лое объемное соетротивление, уравления для Контурюв, содержащих переходы база-эмиттер, можно записаггь

+ ит1п-

Э нас 1

Энас 2

Энас 4

ЭнасЗ

Обозначая

Э нас1 -Э нас гД-Э нас 3 нас

(8.16)

(8.17)

получим Ii/l2=y/{l-y) =7(/y2 yl).

Теперь выражение для пар,аметра у, показанного' на рис. 8.8, можно записать У=у1у2/(lyi+yi)у откуда

{2y-l)=-{Iy,-yIyMhi + yIy,). (8.18)

Поскольку {1у1+1у2)=1Е и (/i-l2)={Qy-1)/о, раЗНОСТНЫЙ ВЫХОДНОЙ ток МОЖНО' 1П)редстав1ить

2) Б

Цусть 1х, /у и Iz обозначают соответственно /о, (/yi-/уг) и (/i-/2), которые пропорциональны параметрам У и Z. Тогда

(1-Y) + (1+Y)/k b

2 - У-1) /о - /о (1 + + (1 . . (8.19)

(8.20)

(1+Г) + (1-Г)/у в

Если транзисторы Ti-Ti имеют одинако|Вую геометрию, характер .распределения .примесей и теМ|Перату1ру п1е|реходов, то у-1 н вышеприведенное выражение можно упростить:

Iz=-Ixlylh- (8.21)

Из выражения (8.21) вийно, что характеристика линейна по отношению к обоим сигналам 1х и /у. Более того, масштабный коэффициент - IIIb не зависит от окружающей температуры. Поэтому данная схема имеет преимущество по сравнению с простой управляемой напряжением схем.ой, показанной на рис. 8.5. Ее

Рис. 8.9. Четы1рехкваира.н-пный перемножитель иа оснШе управляемых током яяффереициальных каскадов -

единственный недостаток заключается ов том, что она является двухквадрантной, так как ток 1х = 1о не может быть отрицатель- ым.

Один из возможных способов устранения такого ограничения показан ва рис. 8.9, где два управляемых током делителя тока образуют четщрехквадрантное устройство умножения. В этом случае

-(1 -yi) /.а = (2Уг-1) 4а-(2У,-1)1.,. (8.22)

Из уравнений для контуров, содержащих переходы база - эмиттер транзисторов Ti-Та и Ти Гг, Г5, Го, имеем

(l.-Yi) + (l+Yi)ai;i--i/2) e - (1+Yi) + (1-Yi)(/!/i-/;.2) e

(I-Y2) + (1+Y2)(/.-Wh (8.23)

(l+Y2) + (l-Y2)(/!/i-W/B где

Yl ~ на с 1-Э н a сг/Э нас 3 нас 4 V2 Энас 1 Энас2/Энас Б Энасб- (8.24)

При выводе выражения (8.23) было принято допущение, что Ti-Гб являются транзисторами с большими коэффициентами усиления и пренебрежимо малыми объемными сопротивлениями. Если они имеют одинаковую структуру и температу|ру переходов, то 71=72=! и.

h-h = [{U~IJ{Iyx-h2)Vlb- (8.25)

Подставляя Ixi-Ix2-Ix, lyi-1у2=1у и /i-hIz, получим

Iz-Ixlylh- (8.26)

В этом случае полярность 1х может быть любой.

8.4. Линейные преобразователи напряжение - ток

Показанный на рис. 8.9 перемножитель имеет один недостаток: необходимость управления от источника тока может вызвать трудности при его применении. Поэтому целесообразно каждый вход дополнить линейным преобразователем напряжение-ток.

Простейшей схемой, которую можно' использовать для этой цели, является дифференциальный усилитель с последовательной обратной связью по току в эмиттерной цепи (рис. 8.10,а). Применяя выражение (4.37) и (4.38) сначала к преобразователю JJx-Ix, получим

Ux=-Ut In (V4i-1) + Rb (2 4i-/o); (8.27)

Vx =г/г1п(/Л.2-1)-/?э(2/.2-/о), (8.28) где/?э:=;?э+ээ+(-бб+7?г)/(1 + Р); /=cl+/r.d=0.

гПри Еывюде этих выражений было- принято, что транзисторы имеют большие коэффициенты усиления (а =1). Суммирование выражений (8.27) и (8.28) дает

Ux=Ut In {IJU) + Я'э (4i - 42)-

Вводя обознаиение Ixi-Ix2=Ix,

[/v l + /x o

= ln

получим 4

. (8.29)

II. О Го

,0м

Рас. 8.10. Лииеииый гареобразюватель нашряжевие-ток та асиове дифференциального каскада с Ш'01Сладо-в.ательН10Й офатной ивязью ио то.К|у в эм.вттер-

ных цеиях:

а-принцивдальна'я схеме; б - йормированная характеристика

Применение аналогичных методов к анализу преобразователя IIy-/у позволяет ползгчить

(8.30)

Несмотря на различие обозначений выражения (8.29) и (8.30) описывают, по существу, одинаковые характе|ристики. Степень нелинейности этих характеристик определяется отношением Ralof Ut (рис. 8.106). Наиболее удобным способом оценки погрешности обусловленной нелинейностью, является нахождение отклонения функции Ix/h=f(.Ux/UT) от функции Ixlh=SToUхЮт, где первая (Ьункция описывает реальную характеристику в соответствии с выражением (8.29), а вторая является ее линейным приближением. Коэффициент

=-i (8.31)

d(U lUj) /Ut.=o 2 + Rglo/Uj,

8тв =

соответствует наклону реальной характеристики передачи в точке Ux/Ut=0. Исходя из этого погрешность нелинейности йнл можно определить следующим образом:

Лнп = Sto Ux /Ut -f {Ux /Ut ) = StUx /Ut -Ix Ho- (8.32)