Метод управляемый источник - многока>1алы1ая обратная связь

о а

S £

Q<Oo

I/ Л. . Л,

ВЫХ

Критерий применения

е < 100, ю < tu*K,/100/),Q

Условия расчета

R, = R, - Rg - R, С, = Сз = С

Параметры схемы

4- К,

, 0 =

1 г

V2(l - К.К.) 4- If,

Исходные данные

Метод бескбнвчиый коэффициент усиления - переменная состояния

с

С,/?,Д.(Ла + R,)

Л (К, + Л,) + 5С,Л,Л,(Ла + R,) + sC.aRiRRR, + Л.)

Критерий применения

Условия расчета

Q < 300,- ю, <- юГ/100>( 0. о < жГ/ЗО Q

Л, = Л, = Л, = Л, 5 = Л, = г. С, = С; = С

Параметры схемы

Исходные данные

в)<. О, Л, г

Метод управляемый источник в неинвертирующем включении

A(.s) =

A(s) =

при <bi >

при Mj < f)

1 + 1{6[сзл, + + лг)] + (с, + с) з} + i {fc[(c, + с,)лз + qrjcjt?, + с.с^л, + RR} + sC,C C,R,Rr3

при > f.j

при (Jj <

Rc.+ R,

Критерий Применения

- о < 3. m, < wf/looe, Rt II д5 < i/looecuoc д. д, < 1/100мрсз

Условия расчета

л,= 2лз= л, с,= с, = -= с

Параметры схемы

Исходные данные

Величины элементов

- - 4 -5-7

при ог > tu ft) - 0)j

for < шо

Данные приведены для случая ш > ; для случая и < uj поменять местами вьшоды хну

Метод управляемый источник в неинвертирующем включенмГ

S к ii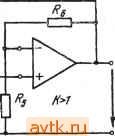

при Oz > CJ,

при ш, < to.

1 + scsc,R;jlR, + д.)

Л, + J?. + + iI(C, + C) (Л, + Л.)Л4 + С,Л,(Л, + R,- KR,}] + AQC, + C,C, + СзС,)ЛэЛ,(Л, + Л,)

Критерий применения

О < 10, о) < tuf/lOO /(oQ

Условия расчета

-4 =

Параметры схемы

л, + л, + R,

\/ CjCj/fiRj

л, + л, +

при OJj > fUj

*Г(Л, + Л.)

Л, + Л, + л.

прн й>, < е>

+1- л:

Исходные данные

си , tuj, е. С, и Л, = 2л„ Сз = гс.

! 3 2

2а) С, 3

- ~23

Метод управляемый источник - многоканальная обратная связь

> 5 -g = се

ffv Сз

А>>7

A{sy

4

Qio, o4 при (u> (t)

---г-5

прнш,<Ше

X, + saCiCfRtiRtR, + Л1Л, + it,itj

Критерий применения

3<е<30. oio=o)f/100K,Q, К,Л„< l/lOOoioC

Условия расчета

3/{,= X, С,= 4С, С,= С. С,= 5С

Параметры схемы

к, + л 2 - ЛГ,,

2RC IRCyja

при 0>, > Шр

при lUi < big

J 2 - JC.JC,

8- зд:,

Исходные данные

240 + 2-2У240+ 19 У2+ЛГ.О 1 (а>, --90 2До>, ° 2 + Л:,6 U.

обеспечивают больших значений Q, если только х инвертирующие усилители имеют небольшие коэффициенты уоиления.

iB фильтрах, построенных на основе второй разновидности этого метода, коэффициент, одределяющий добротность, представляет собой разность в знаменателе соотношения для передаточной функции. Повышенная чувствительность к разбросу параметров элементов обычно компенсируется менее жесткими требованиями к коэффициенту усиления.

Третья разновидность является комбинацией двух первых. В базовых схемах используются как инвертирующие, так и неинвар-тйрующие усилители. В результате требования к разбросу параметров оказываются менее жесткими, чем в случае второй разновидности метода, а требования к коэффициенту усиления менее жесткими, чем в первой. Фильтры, построенные на основе комбинированного метода, рекомендуется применять, если необходимы высокая точность и/или большие значения добротности.

Если ОУ используется в качестве преобразователя иммитанса, то требования к допускам на параметры элементов оказываются нежесткими, но непосредственное каскадное соединение становится затруднительным, посколБку базовые схемы имеют низтое входное и высокое выходное сопротивления.

Схемы, построенные на основании р а осмотр еиных методов, почти эквивалентны. Выбор схемы, наиболее подходящей для решения конкретной задачи, зависит от разработчика. Результаты расчетов наиболее расиространенных базовых схем приведены в табл. 7.13-7.24. В них значения свободных параметров Bbii6ipaiHbi таким образом, чтобы чувствительность к разбросу параметров была низкой, а отношения значений параметров элементов - оптимальными. .

7.6. Чувствительность

Фактическая харакгеристика активного RC-фшьтра всегда отличается от расчетной передаточной функции A{s). Это обусловлено разбросом параметров элементов и влиянием внешних факторов (температуры п т. п.). Относительная чувствительность к разбросу параметров или внешним воз;действия!м на t-й элемент определяется выражением

(с dA(s)/A(s)

i д In Wi dWilWi

, щ дМ (7.12)

A{s) dWi

Передаточную функцию Л(8)=Л(]£1)) можно представить АЧХ Л(ш) I и ФЧХ arc Л.(сй). Их относительные чувствительности определяются действительной и мнимой частями выражения (7.12)

Im5 (jco,,)=t;IHAii. . (7.14)

Если относительное изменение Awt/Wi мало, то имеем

A\A(jco)\/\A{ici>)\[ReS Qw,Wi)]iAWi/Wi); (7.15)

Д arc Л (j со) ж [Im (j со, wt)] (Д ш^М). (7.16)

Распространяя эти выражения на случай одновременного изменения значений п элементов, когда wi=Ru R2, .... Ci, С2, ... - -, 1, Кг, - , получим

lM V[Re5(jco,a;,)]; (7.17)

Д а?с А (j со) 2 (j со, и>д] . (7.18)

i=i

Если небольшие относительные изменения являются случайными (рааброс параметров) и можно считать, что их абсолютные значения меньше, чем Awio/Wi (технологический разброс), справедливы следующие выражения:

АИ(] Ц)1

[ReS;.(jco,t.,)f() ; (7.19)

Д are Л (] со) W / Y [Im S;, (jco, wd? (- Y! (7-20) U=i \m J )

Вычисления no четырем последним выражениям обычно Tipy-доемки и требуют использования ЭВМ. По этой причине часто целесообразно оценить частотно-зависимую чувствительность передаточной функции Л(5)=Л(](о) путем рпределения частотно-независимых показателей чувствительности параметров Ло, шо и Q для каждой базовой схемы, из которых построен фильтр. С помощью показателей чувствительности

0 Swi i too rfai

£ Q dwi -

можно сравнивать базовые схемы и получать грубые приближения частотно-зависимой чувствительности всей передаточной функции Л'(5). Их можно рассчитать на основании тех же общих выражений, которые применялись для определения параметров передаточных функций базовых схем, представленных в табл. 7.13-7.24, но dftn не учитывают особенностей расчета, указанных в этих таблицах. (Таблицы предназначены для получения передаточных функций.при определенных условиях расчета и не содержат этих выражений. В таких случаях расчет чувствительности должен начинаться с о^пределения полной передаточной функции.) , . -

7.7. Частотные характеристики ОУ

Разброс параметров элементов не является единственным фак-тором, который обусловливает расхож,дение между расчетными и фактическими характеристиками. Аналогичные последствия вызы- вает частотная зависимость параметров ОУ. Для определения этого влияния потребовались бы машинные методы анализа. Если же в фильтре иоиользуется один ОУ и коэффициент усиления петли больше 10, относительные погрешности можно оценить на основании приближении, рассмотренных в § 6.3.

Применяя выражение (6.48) к анализу АЧХ, получаем

haHfReh(s)0,5\h{s)\ (7.22)

где

/г (S) = [1 + Т (s)]-i = [ 1 + А As) Р (s)]-\ S = j со. (7.23) Поскольку

T(jco) = T(jco)eP =ЛЛ1 )11Ра )1е'< + е), (7.24)

2 1+2Гаи)с05ф5- +

(7.25)

Если коэффициент усиления петли значительно больше 1, выражение (7.25) можно упростить:

1 1 , cos фу

2 r(j(o)

2 [Hu{icu)P(iw)P

С05(фд 4-

zo о

-zo во

Ю' 10 70 70 70 т

Mo{Jw)IIP{Jw)l

(7.26)

Рис. 7.7. Пофешности вдаэф-фвциента усиления

О -90

-180

10 70-

7* 10 т

применив аналогичным образом вьцражения (€.49) .к фазовой характеристике, получим

Im h (s)

Рй ( ) == -arctg = arctg

1 -Re/i(s) sin фу

s=i (0

(7.27)

r(] cй)+cosфJ,

Если коэффициент петли значительно больше 1, получим

<р, (со) arctg Р^ = arctg +Фв) . (7.28)

12-136 353 . .

Таким образом, если известны АЧХ и ФЧХ аперационного усилителя с KqppeHHHeft и цепей обратной связи, то выражения (7.26) и (7.28) дают хорошие .приближения .погрешностей по ам!П-литуде и фазе. Вычисления оказываются наиболее простыми в том случае, когда Л (0)) ~,l/p(jco), т. е. когда может быть найдено соотношение 1параметров цепи обратной связи с желаемыми характеристиками фильтра (рис. 7.7). В § 5.5 было показано, что при правильно рассчитанных .цепях коррекции ОУ наклон его АЧХ обычно составляет -20 дБ/дек, а .фазовый сдвиг <рл= -90°.

7.8. Настройка

Настройка а.ктивно.го фильтра заключается в поочередной проверке .и настройке входящих в него базовых схем по па.раметрам Ло, (Не, (i>z, (йо и Q. Первые три параметра м'Ожно ивмдрить непосредственно, а два последних определить по АЧХ и ФЧХ настраиваемой базовой схемы.

iB простых базовых схемах ФНЧ BiTOporo порядка о не зависит от Q, и ее можис npioBqpnTb путем измерения значения Юоо в точке -40 дБт в которой lF(j(o) ] =0,01. При Q>l/Ke значение Q можно определить по всплеску АЧХ

. \Р(1 (0) = 2Q2(4Q-l)-V (7.29)

измеренному на частоте

(о^=(Оо (1-1/2 0)1/2. (7.30)

. Добротность Q<1/ можно определить по предельной частоте, которая изменяется в зависимости от Q в соответствии с выражением

с =(йо{1-1/20 + [(1-1/2 Q2)2+i]i/2}i/2. (731)

В базовых схемах ФВЧ второго порядка парамепры т и с в выражениях (7.30) и (7.31) преобразуются в соответствующие сопряженные параметры, а выражение (7.29) остается без изменений.

Частоту о базовых схем эллиптических фильтров второго порядка можно найти как частоту, на кото.р|ой фазовый сдвиг равен 90°. Добротность Q таких фильтров контролируется по величине

/=(] о)1-0[1-(сОоед. (7.32)

Частоту (йо базовых схем полосовых фильцров можно проверить посредством измерения фазового сдвига на этой частоте. Коэффициент усиления на частоте юо должен равняться Ло. В за- висимости от знака Ло фазовый сдвиг должен равняться нулю или 180°. Поскольку

(сояг-юях)/ 1/ (0я2 Я2 = Ш (7.33)

значение Q можно определить путем измфения относительной ширины диапазона частот на уровне -3 дБ.

Элементы схемы, влияющие на заданный параметр базовой схемы фильт|ра, и последовательность операций настройки можно' выбрать при помощн выражений, приведенных в табл. 7.13-7.-24.. Эти выражения связывают параметры схемы и элементов базовых схем фильтров.

7,9. Примеры расчета

пример 1. Требуется -рассчитать ФНЧ, у -которого макоималшо плоская ча-стотная характеристика второго шорядка -обеспетвает единичный коэффициент усиления IB полосе пропускания и ан=-О'.б дБ щри н = 1 кГц.

Из табл. 7.2 имеем Ен = 0,349. Подстановка этого значения в выражение (7.3) дает Сйс=2я-.1693 c-. Из табл. 7.3 имеем: сйо=-10636 c- -и Q=0,7071!l.

Поскольку At, .и Q .малы, приемлема простая схема, триведенная в табл. 7.13 (-рис. 7.8). Задаваясь для .расчета i?i=i?2=10 .кОм и К-1, получим: Ci = =2Q/tooi?= 13,29 -нФ, C2=.l/2Qtoo/?=6,684 нФ, /?з=оо, /?4 20 кОм. Фильтр будет иметь сл.едующие параметры:

Л = /С; (Оо = (1 2 Ci С2)-1/2 ;

Подставляя эти та-раметры в выражение (7.21), получаем: = = S = == - - ;

лл! \2 -1 -2 о

cuo/?iC3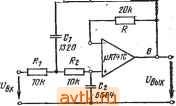

Р.И!С. 7.8

cOo Ca

S =l.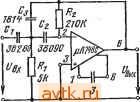

20 0

W 10 10 70 70? Wf/a. .f)

1(2*

Рис. 7.9 355