Фильтры Томсона. АЧХ этого фильтра определяется выражением

T(co) = Re-ii ds

г) .

.=0 /2

(7.10)

S=j<b

Фильт|р обеспечивает максимально ,плоскую аппроксимацию идеальной ФЧХ. Его целесообразно применять в тех случаях, когда к избирательности предъявляются не очень жесткие требования, но требуется хорошее качество переходного процесса.

Расчетные характеристики фильтра Томсона приведены в табл. 7.12. По данным табл. 7.11 можно определить порядок фильтра, при кбтором пульсации АЧХ и ФЧХ не превосходят заданные.

7.3. Аппроксимация передаточных функций . , фильтров верхних частот

Xaipактеристики ФНЧ, рассмотренные в § 7.2, можно преобразовать в характеристики фильтров верхних частот (ФВЧ) путем подстановки комплексной частоты S=l/s. Тогда частоты ©£, ©о и fDz из табл. 7.3-7.12 будут соответствовать сопряженным параметрам l/ft)£, l/fDo и 1/(Вг. Значения добротностей остаются при этом неизменными, а значения параметров ФВЧ можно определить по значениям параметров ФНЧ, приведенным в табл. 7.13- fl6.

Требуемый порядок фильтра п можно определить на основании З'словий для низкочастотных аналогов, рассмотренных в § 7.2.

7.4. Аппроксимация передаточных функций

полосовых фильтров

Полосовой фильтр имеет одну полосу пропускания и две полосы подавления. Первая из них находится между нижней ©hi и верхней (Вн2 предельными частотами, а две последние расположены в диапазонах от нуля до ©ci и от (осг до оо соответственно. Дополнительной характеристикой, представляющей интерес, является так называемая центральная частота, которая обычно

определяется следующим образом: (Вм = 1юн1©н2- Порядок расчета зависит от относительной ширины полосы пропускания В = = (©н2-©Hi)/©Ar. Если значение В велико, то задачу построения фильтра можно решить путем каскадного включения ФВЧ и ФНЧ. При средних и малых значениях В простейший способ заключается во введении следующего преобразования комплексной частоты:

Фильтр нижних частот второго порядка

Управляемый источник в' неинвертирующем включении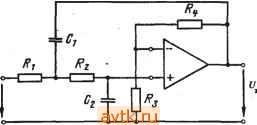

К = 1 +

1 + i[Cj(*, + + (1 - К)С,Л,] + J=C,Cj,R,Aj

Критерий применения

Условия расчета

О < 3, й) < Г/100С

G < 3, и„ < w,*/100/4 0

С,= С

3 < G < 10, < < tu*/IOO-4eO

Л.= ЮЛ, Q=0,1C.

Параметры схемы

А„ = К, Оо

гл-к

Исходные данные

Л., о, G, С

t o, О. Rl

Величины элементов

2Q to R 1

2QeoR

2Qco C

wlC-R

Фильтр нижних частот второго порядка

Таблица 7.14

Метод бесконечный коэффициент усиления - одноканальная обратная связь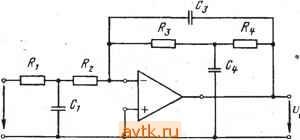

при С.(Л, II Лз) = С/Л, II R,)

AU) = -

3 + 4

1 I + sc,{R,\\ r;)

Критерий применения

Условия расчета

Q < 10, \ A,Q\ < 100, О), <<у'/100Л|С

+ д 1 1

Параметры схемы

Исходные данные

Ао, (Оо, Q, С,

Величины элементов

Q=4C=C3, R= R= =

R . I Л!

Фильтр нижних частот второго порядка

Таблица 7-15

Метод бесконечный коэффициент усиления - многоканальная обратная связь

1 I

Си в>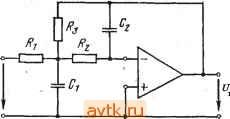

.4(.v) =

> (v) = -

Критерий применения

е < 10, I A Q\ < 100, (о„ < о>*/100 ! .4 ! О

Условия расчета

Лз= (1 + Мо1)К=

-4 = - ft>o

Параметры схемы

1 1

Исходные данные

0. o. G. с,

4G4I + Мо1)

fijflCi

II г?

3 £

г

ъ

Принципиальная схема и передаточная функция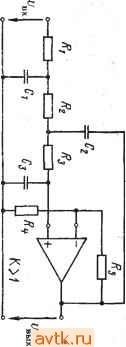

а

а

S=0+j<b.

(7.11)

в этом случае логарифмическая АЧХ оказывается симметричной относительно центральной частоты (Им- На практике процедура расчета включает этапы определения па1раметров эквивалентного ФНЧ, аппроксимации его передаточной функции в области нижних частот и получения необходиЫго распределения полюсов и нулей передаточной функции полосового фильтра с использованием преобразования в соответствии с выражением (7.11). В результате п полюсов и т нулей эквивалентной передаточной функции будут преобразованы в (м-т) нулей исходной функции: каждый действительный полюс - в пару сопряженных полюсов, а каждая пара сопряженных корней - в две пары сопряженных корней. Последним х этапом- является нахождение параметров- элементов на ос- - новании полученного распреде- Ривс. 7.3 ления нулей и полюсов.

Если значение В достаточно мало, указанное преобразование комплексных величин можно упростить и заменить преобразованием Скалярных величин q= (а>н2-(>>т)12 и последующим' перемещением по вертикали на величину юм, как показано на рис. 7.3.

7.5. Реализация фильтров на основе ОУ

ОУ в активном /?С-фильтре можно рассматривать как управляемый напряжением источник с конечным или бесконечным коэффициентом усиления или как преобразователь отрицательного иммитанса. Управляемый источник может работать с одной или несколькими цепями обратной связи.

Применение-метода усилитель с бесконечным усилением и одноконтурной обратной связью иллюстрируется рис. 7.4. В этом случае передаточные функции определяются отнощением последовательной входной проводимости Уг1 к проводимости обратной связи Yt2. По существу, схема представляет собой инвертирующий усилитель с офатной связью. До тех пор пока коэффициент усиления петли достаточно велик, передаточная функция определяется только пассивными элементами. Необходимый коэффициент усиления Ло .можно задать посредством .выбора относительных

значений сопротивлений входного двухполюсника и двухполюсника об]ратной связи. Схема имеет два недостатка: число пассивных элементов велико, если необходимые З1начения коэффициента усиления Ло и/или дофотности Q велики, то иарамецры элементов будут существенно отличатвся друг от друга.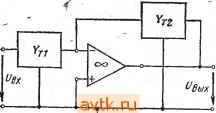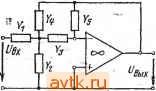

- - /!(S}=-Yr,/yrz

7.4. Метод беононсчный коэффициент уоил€1Нйя-юдноканальная юб-1ратная йвязь

Рис. 7.6. Метод !бебконечный коэффициент уоилевия - (меогоканаль-на я !0рагрная вязь

Метод усилитель с бесконечным усилением и многоканальной обратной оБЯВью (рис. 7.5) имеет преимущества по сравнению с предыдущим: во-первых, схема достаточно простапо сравнению со схемой на рис. 7.4, во-вторых, если требования к Ло и Q не очень жесткие, допускается больший разброс параметров элементов, а их номинальные значения отличаются в меньшей степени, чем в предыдущем случае.

Еще одним методом, представляющим интерес, является метод усилитель с бесконечным усилением в схеме с переменной структурой . Он заключается в использовании' двух ОУ в качестве интеграторов и третьего - в качестве усилителя с обратной связью.

Он применим на средних частотах и обеспечивает высокие значения Q в дополнение к весьма б^рагоприят-ным требованиям к разбросу параметров.

Принцип применения метода регулируемого источника поясняется на рис. 7.6. Поскольку в этом случае обратная связь является частотно-независимой и отрицательной, ОУ действует как управляемый напряжением источник напряжения. Этот метод имеет три разновидности: управляемый источник в инвертирующем режиме , управляемый источник в неинвертирующем режиме , управляемый источник с многоканальной обратной связью .

Фильтры, построенные на основе первой разновидности метода, не очень чувствительны к раэбросу параметров элементов, но не

1/а

К

Рйс. 7.6. Метод регулируемого источвйка

е

е

J>9

Е

>1

5в

>!

Принципиальная схема и передаточная функция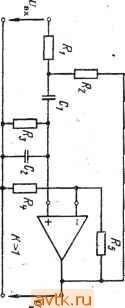

й

р

Принципиальная схема и передаточная функция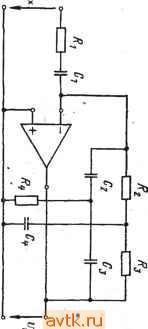

ё

И

Метод бесконечный коэффициент усиления - многоканальная обратная связь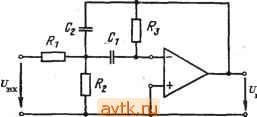

sCtR,R,

Ri + Rt + i(C, + CRiR, + sCiCtXiRiRt

Критерий применения

Условия расчета

С<10, 0)0 = й>Г/100/1 е

Л. С,

Л, С, + с,

е=

Параметры схемы -

Мо1> С Л2= 00

Исходные данные

Ао,о) , Q, Л,

6 п M.I р