кадного включения цепей, имеющих передаточные функции более низкого порядка, в соответствии с соотношением

His) His) Hi(s) .

Базовые функции

Таблица 7.1

Функция

Об?Г значение

Характеристические пара -метрь(

Расположение нулей и полюсов'

Фильтр нижних частот первого порядка

Филыр верхних частот первого порядка

Фильтр нижних часто! второго порядка

Фильтр верхних частот второго порядка

Qa) <ol

Эллиптический фильтр второго порядка

5 S*

Фильтр нижних частот третьего порядка

l+)f

Фильтр верхних частот третьего порядка

A(s) =

00 5

Полосовой фильтр второго порядка

A{s)-.

0>о

у

Zcosip Z6j

Таким образом, передаточные функции первого, второго и третьего порядков следует рассматривать как базовые функции, а реализующие их активные цепи - как базовые цепи.

Схема, с помощью которой реализуются основные передаточные функции, обычно содержит несколько свободных параметров, что, во-первых, позволяет получить ряд эквивалентных схем, а во-вторых, путем изменения свободных параметров выбрать коэффициент усиления и/или осуществить оптимизацию чувствительности.

Активные фильтры, использующие интегральные ОУ, обычно имеют большое входное и малое выходное сопротивления. Благодаря этому возможны независимый, расчет и настройка, а также непосредственное соединение базовых цепей.

Наиболее распространенные базовые цепи приведены в табл. 7.1. Здесь Ло - коэффициент усиления в полосе пропускания; (Не - характеристическая частота функций первого порядка; с)о - частота, соответствующая полюсу, coz - частота, соответствующая нулю; Q - коэффициент добротности.

- Нули и действительные полюськ можно представить соответственно параметрами coz и сое, а пары сопряженных полюсов ©о и Q, как показано на рис. 7.1.

Каждую базовую функцию .можно реализовать при помощи соответствующей jRC-цепочки. С целью эко- . *

-номИИ ОУ функция первого поряд- р, 7 1 .Пара соцряженных ка обычно объединяется с функцией комплеисных полюсов

второго и при помощи одного активного элемента реализуется полученная таким образом функция третьего порядка. Другой распространенный способ заключается в том, что для реализации функции первого порядка используется пассивная 7?С-цепочка, .подключаемая к выходу активного фильтра.

г ...

7.2. Аппроксимация передаточных функций фильтров НИЖНИХ частот

Исходными для расчета фильтров нижних частот (ФНЧ) обычно являются заданные АЧХ или фазочастотная характеристика (ФЧХ). Основные характеристики, показаны на рис. 7.2. В большинстве случаев параметры даются в нормированном виде, причем нормирование осуществляется по отношению к коэффициенту усиления Ло и характеристической частоте (шс или сон), а ослабление на частотах сон и определяется параметрами, приведен-ными в табл. 7.2: ен= Кап111од(ан/10)-1 и es= = К antilog(as/10)-1. .

Фильтры Баттерворта. Фильтр Баттерворта, у котарого все первые 2п-1 производные передаточной функции по частоте to при нулевой частоте равны нулю, имеют АЧХ

1/ (] (0) I = f 1 + ((о/(Ос )2 ]-V2, (7.1)

являющуюся максимально плоской аппроксимацией идеальной амплитудной характеристики. Все п полюсов его передаточной функции всегда располагаются в левой полуплоскости на полукруге радиуса шс.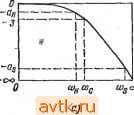

а

Рис. 7.5. Характеристики фяльтра нижних частот

Таблица 7.2

Независимо от значения п на частоте сй=а)с коэффициент уьи-ления всегда соответствует Gh--3 дБ. На частоте, превышающей тираничную, коэффициент усиления снижается со скоростью - 20 дБ/дек.

Фильтры Баттерворта целесообразно использовать в тех случаях, когда АЧХ должна быть монотонной, к избирательности предъявляются не слишком жесткие требования и допустимы выбросы на переходной характеристике.

Основные параметры, характеризующие свойства фильтра Баттерворта, приведены в табл. 7.3. Они представлены в виде функции п и нормированы по отношению к сос. Первая может быть определена из условия

n>Ig -

а последняя - из условия

(7.2)

(7.3):

Характеристики фильтра ваттерворта (и^ = 1)

Таблица 7.J

о

\F[juy)\,AE О

-П -БО.

0=5 \\

Фильтр Чебышева. АЧХ фильтра Чебышева, определяемая выражением

1а >)1=[1 + е2й7((о/(Оя)]-Ч . (7.4)

T (ft)/cuw) = cos[narccos((o/ft)/i)], (7.5)

представляет собой аппроксимацию идеальной АЧХ с равномерными пульсациями. Все п полюсов передаточной характеристики фильтра расположены в левой полуплоскости на полуэллипсе. Пульсации постоянны только в полосе пропускания. На частотах ниже (Он амплитуды изменяются в диапазоне от 1 до \lV а на частотах, превышающих (Он, они меньше соответствующих амплитуд фильтра Баттерворта на [( -l)6--201geH] дБ.

Фильтр Чебьццева целесообразно применять в тех случаях, когда изменение полосы пропускания допускается в определенных пределах, ослабление в полосе подавления должно быть довольно большим и к временньш характеристикам цредъявляются не очень жесткие т|ребования.

Обобщенные характеристики фильтра Чебышева приведены в табл. 7.4. Параметры представлены в виде функции порядка фильтра п:

n>lg-/lg- . (7.6)

Обратные фильтры Чебыш^на. АЧХ обратного фильтра Чебышева . .

1 + егн

(7.7)

представляет максимально плоскую аппроксимацию идеальной АЧХ в полосе пропускания и аппроксимацию с равномерными пульсациями в полосе подавления. В преобразованном диапазоне частот s=(Os/s полюсы соответствующей передаточной функции располагаются в левой полуплоскости на полуэллилсе, а нули - на мнимой оси частот.

Характеристики обратных фильтров Чебышева приведены в табл. 7.5-7.7. Порядок фильтра п можно найти из соотношения (7.6).

Фильтр Кауэра. АЧХ этого фильтра описывается выражением

\Р{](и)\=11 + г^н Ч^п (cй/fi)я)]-l/ (7.8)

где Wn - параметр фильтра, определяемый эллиптическими функциями Я'коби.

АЧХ является аппроксимацией идеальной амплитудной харак-теристики с равномерными пульсациями не только в полосе пропускания, но и в полосе подавления. Соответствующая фильтру Кауэра эллиптическая аппроксимация обеспечивает минимальное

Характеристики фильтра Чебышева (со =1)

Таблица 7.ч

Окончание табл. 7.4

\Fi ff

\FUw)\.p.E ff

О

\F(M\,ti6

U) =7 <x>

-oo 0

W =1 oo.

Wfi7 , oo

1аолица 7.5

Характеристики обратного фильтра Чебышева третьего порядка (ul)

\F[Jw)\,mE Щ

-oo 0

no сравнению с рассмотренными ранее фильтрами отношение (nsldiH при заданных значениях as и ан-

Значения основных параметров фильтра даны в табл. 7.8-7.10. Порядок фильтра п можно найти из соотношения

- >Ainlln-. (7.9)

COg -Off

Характеристики обратного фильтра Чебышева човертого порядка ( = 1)