ми шумовыми свойствами. Это противоречие можно устранить путем использования усилителя в инверсном включении (рис. 6.14а), когда в цепь обратной связи включаются низкоомные резисторы. Поскольку коэффициент шума зависит только от сопротивления источника сигнала, входное сопротивление будет равно сопротивлению Ra.

Рис. 16.114. Уюишиггели 1перем.е|Нно-го №ока на оснюве неинйергирую-щих ОУ 1С юфагшюй связью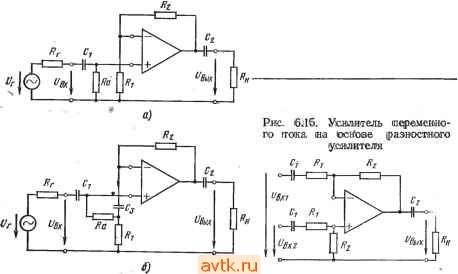

Простой способ увеличения входного сопротивления неинвертирующего усилителя переменного тока заключается в применении последовательной обратной связи по напряжению, как показано на рис. 6.146. Здесь

/?вх=(а11вхд)0+>4 Р). (6.75)

На низких частотах конденсаторы связи Ci и Сг приводят к уменьшению коэффициента усиления. Частотная характеристика определяется передаточной функцией

(6.76)

ОСОщ + Я щ + s

где Aug - коэффициент усиления усилителя с обратной связью на средних частотах, ац - граничная частота входной цепи связи, 0)2 - граничная частота выходной цепи связи.

Если (й>> 1 и fo G)2, то ошибки по амплитуде и фазе в соответствии с этим выражением запишутся

ft (со) -0,5 ( )i/ ))2-0,5 {(ojf, (6.77)

(и) = arctg (©i/©)+arctg (©g/o)). (6.78)

Последовательная обратная связь также не является частотно-независимой, что обусловлено емкостью конденсатора Сз. Это при-

(а1/?вхд)-

(6.79)

водит к тому, что, во-первых, входное сопротивление оказывается частотно-зависимым'в соответствии с выражением

l+Aa + sCsiRi + R)

Во-вторых, при уменьшении частоты коэффициент усиления будет снижаться в соответствии с выражением

Ли is) = [l+s с, (R, + R,)yii + s С, R,l (6.80У

На рис. 6.15 показана схема разностного усилителя переменного тока. Для предотвращения снижения коэффициента подавления синфазной составляющей сигнала на низких частотах оба конденсатора связи должны иметь одинаковые емкости. В противном случае рассогласование возникнет как раз на той частоте, на которой должна подавляться нежелательная составляющая напряжения.

6.6. Источники тока

Р1нтегральные ОУ пригодны для построения управляемых напряжением источников тока с практически бесконечным внутренним сопротивлением. Простейшим вариантом такого источника является инвертирующая цепь с обратной связью, показанная на рис. 6.16а.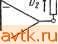

RfR

RcfBjWRi

Вых

й) 6) В)

Р.ИС. 6Л6. Июточвиии TtoiKa с (плавающей нагрузкой

При /?вых = 0 и /?вхд=оо напряжение на инвертирующем входе

Ubxk={R2Ubx + RiUbux)I{Ri+R2)- Поскольку Ubxh = 0, ТО г7вхи=* = -f/Bb,xM (s), откуда С/вхи = /?2/вх/{/?2 + ?1[Ц-Л„(5)]}.

Протекающий через резистор нагрузки R2 ток определяется выражением

/2 = (/вхи-/вых)/2=-/вхи[1+4( №, .

t/в

.t/в

Ri l + R2/[RiO+Aum Ri Таким образом, проводимость прямой передачи равна

S = - t/вх Rl i + RJlRiO+Aum

(6.81)

(6.82)

, Выражение для определения выходного напряжения источника можно записать: /?выхи =-2бых 2и Подставляя Ui-hRz из выражения (6.81), получим

1 I+2/[/?l(l+ (s))] Тогда t/2Bbix = -[/вх[1+Л,г(5)].

Поскольку /2н =Vbx/Ri, то выходное сопротивление источника RBuxu = Rii + A(s)). (6.83)

Р1з этого выражения следует, что при больших значениях Auis) сопротивление 7?выхи может быть очень большим. (На низких частотах типичное значение Л„ равно lO-f-lO. Тогда при Ri = l кОм выходное сопротивление может достигать 10-f-lOO МОм!)

Допущение Явик=0 на самом деле не снижает точности вышеприведенных выводов, поскольку в схеме на рис. 6.16а небольшое сопротивление Rbux включается последовательно с Rbuxu-

В связи с тем, что источник тока предназначен для поддержания постоянного значения тока, протекающего через меняющееся сопротивление нагрузки, обычно допускается выбор Ra=0. При этом компенсация влияния входного тока покоя не дает желаемого эффекта, поскольку значение Ri переменно.

В схеме на рис. 6.16а весь ток нагрузки h протекает через резистор Ru а следовательно, и через источник управляющего сигнала. В некоторых случаях целесообразно включение усилителя по неинвертирующей схеме, как показано на рис. 6.166. При этом входное сопротивление велико, а ток нагрузки замыкается на землю через резистор Ri.

Схема на рис. 6.1 бе в некоторых отношениях сочетает преимущества схем, показанных на рис. 6.16а, б. Здесь усилитель используется как инвертирующий. Следовательно, конечное значение коэффициента подавления синфазной составляющей сигнала не приводит к появлению погрешности. Цепь тока нагрузки замыкается через резистор Ra.

Ток, протекающий через резистор нагрузки R, имеет две составляющие: U = l2 + h- Поскольку /2= [1+Л„(8)][/вхи ?2 И /3 =

= -UbuxIR3=Au{s)UbxuIR3, ток /4 можно опрсдслить приближенно

Вследствие того, что при Лм(8)>1 Ri[l+Au{s)]:>R2, ток /4 зависит только от сопротивлений Ri, R2 и R3 в соответствии с выражением

Ri R2\\R3 + R2/[Ri( + Aum

При этом рекомендуется значения R2 и R3 выбирать такими, чтобы R3<.R2. Тогда через нагрузку будет протекать ток

h тЛ , .J......... (6.85)

Можно показать, что выходное сопротивление источника тока будет соответствовать

выхи 1?з(1 +AAs))/{Ri + R2)- (6.87)

Ввиду того что /?з<С/?2, сопротивление по постоянному току со стороны инвертирующего входа равно Ri\\R2. Поэтому влияние входного тока покоя можно скомпенсировать при помощи резистора Ra = Rl\\R2.

Максимально возможное падение напряжения на резисторе нагрузки меньще выходного напряжения ОУ на значение, равное падению напряжения на резисторе R3. В связи с этим сопротивление резистора R3 желательно выбирать так, чтобы падение напряжения на нем не превышало 0,2-0,5 В.

Общий недостаток всех трех рассмотренных схем заключается в том, что нагрузка не присоединена к земле. Схема источника тока, нагрузка которого может быть заземлена, показана на рис.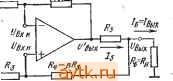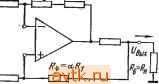

a) S)

Рис. 6.17. Источники тока с заземленной наг-рузКОЙ

6.17G. Р1з уравнений для узловых напряжений, которые могут быть записаны для входов усилителя, имеем

t/Bxn = (at/Bxl+t/Bb,x)/(l +а). /вхн = (Р^/вх2 + /вых)/(1+Р).

где

вых~и(*) (fBXH - вхи) и^ых - б Re-

Выходной ток определяется выражением

/б = /4 + /5 = (/вх2-/вых)/[з(1 +Р)] +(/вых-/вых)/5,

которое можно переписать

вых ~ h~

{[1 -Ь а+Ад (S)] /?5 + Ли (S) (1 -Ь а) Р Rb} Ubx 2 - (s) (1 + P) R3 ъх i

[1 -Ь a -Ь Л„ (s)] IRs Rb{l+ ?>)+Rb Re+Rs Re (1 + P)] - Ли (s) (1-1-a) Rg R

(6.88)

Из этого выражения следует, что значения чувствительности по разным входам усилителя неодинаковы. Характер изменения тока h таков, что выходной ток оказывается зависимым от сопротивления нагрузки Ri. Следовательно, источник тока имеет конечное выходное сопротивление. При Л„(5)>1 отношение напряжения 229

холостого хода к току короткого замыкания можно приближенно записать

бых и 1 (3 + 4)/[(4 + 5) 1-2 =

= 5з(1+Р)/[?5 + зФ- )]- (6.89)

Выходное сопротивление можно сделать бесконечно большим, выбрав значения аир такими, при которых знаменатель выражения (6.89) равен нулю:

а-р = 7?5/7?з. (6.90)

Поскольку сопротивление R5 обычно меньше R3 по крайней мере на два порядка, а должно превышать р не более чем на несколько десятых процента. Необходимо также, чтобы Ri\\R2= =R3\\Ril в противном случае влияние выходного тока покоя нельзя скомпенсировать. Так как а~р, это условие может быть выполнено при 7?1=/?з.

Для того чтобы выходное сопротивление было бесконечно большим, необходимо поддерживать постоянным расчетное значение разности между аир. Этого легко добиться при помощи показанной на рис. 6.176 схемы, в которой Ri=R3, а=р (следовательно, R2=Ri) и последовательно с R2 включен резистор Rs так, что

вых uRbRi (R3.+RMiRi+Rb) Ri-iR+Rb) R3] = RbH, (6.91)

где H - коэффициент подавления синфазной составляющей напряжения в цепи, состоящей из Ru R2+R5, Ra и Ri+Rs-

Теоретически Rbuxu можно сделать бесконечно большим, однако вследствие разброса параметров элементов и небольшого сопротивления R5 оно всегда будет меньше выходного сопротивления ранее рассмотренных схем.

Допуски на параметры элементов можно учесть путем подстановки Ri{l+k), aRiil-k), Riil-k) и a/?i(l-f-) вместо Ru R2, Rs и Ri. Тогда

выхи 5. (.92)

Хотя теоретически выходное сопротивление, зависящее от разброса параметров элементов, можно сделать бесконечно большим за счет подбора сопротивлений Ri-~-R4, практически оно всегда оказывается конечным. Более опасен однако другой недостаток, заключающийся в том, что при неблагоприятном сочетании параметров выходное сопротивление может оказаться отрицательным. При отсутствии сопротивления нагрузки это может привести к возникновению нежелательных колебаний. Поскольку выходное Сопротивление является частотно-зависимым, может быть обеспечена динамическая устойчивость, т. е. высокочастотные колебания могут быть устранены путем подключения корректирующего конденсатора параллельно резистору R2.

Если считать, что условие (6.90) выполняется, то, воспользовавшись выражением (6.88) для расчета выходного тока, получим

(6.93)

Из этого выражения видно, что проводимости прямой передачи неодинаковы. Однако, до тех пор пока RilRs, эта разница пренебрежимо мала и можно считать

= a(f/bx2-f/Bxi)/6- (6.94)

Рис. 6.118. Иеточтак тока с заземленвой нагруэмой (схема Хауленда)

Ток, создаваемый источником, может иметь положительную или отрицательную полярность относительно земли. Единственным фактором, ограничивающим его максимальное значение, является допустимый ток интегрального ОУ. Максимальное падение напряжения на нагрузке меньше мак- %zo-ci: симального выходного напряжения ОУ на 1 значение, равное падению напряжения на резисторе Re.

В некоторых случаях целесообразно применение так называемой схемы Хауленда, показанной на рис. 6.18. Здесь

и = (f/вх 1 R2 + t/вых RMRl + R2) = (а f/вх 1 + /вых)/(1 + а), /5 = /з + /4 = (t/вх 2 - t/вх М + (t/вых - t/вх )/Р 3. t/вых = AuXs) (f/вх и- t/вх и), t/вх u = hRb-

Ркпользуя ЭТИ соотношения для определения тока, протекающего через резистор Rs, т. е. выходного тока источника, получим

вых ~ь~

P(l-ba + >4 (s))t/bx2- u(S)t/bl ggg.

Далее, поскольку а=р, An(s) > (1-f-a) и Л„(5)/?з>/?5(1-1-а) X Х(1 + Р), можно записать

/вых = h :(t/bx2-t/bxIRz- (6.96)

Выходное сопротивление относительно точек, к которым присоединен резистор Re, определяется отношением напряжения холостого хода к току короткого замыкания

/?вых и = [ 1 + а + Л (S)] Р [(1 + а) (1 + Р) + (s) (Р-а)]-1

~/?зР/(Р-а). (6.97)

Из этого выражения можно сделать два вывода. Во-первых, выходное сопротивление велико, если а^р. Во-вторых, значение вых и прежде всего зависит от разброса сопротивлений резисторов. В наихудшем случае, когда i=/?i(l-f-!fe), R2=aRx(\-k), /?з = ~R\{\-k) и /?4=a7?i(l-f), получим приближенное равенство

/?выхи /?з/4. (6.98)

Выходное сопротивление всегда можно сделать бесконечным посредством подбора сопротивления одного из резисторов Ri-i-Rt. Для исключения возможности потери устойчивости вследствие возникновения высокочастотных колебаний резистор R2 следует за-шунтировать конденсатором небольшой емкости.

Отличительная особенность этого источника состоит в том, что при [/вх1 = 0, [/вхй=[/вых=юоп51 И а=3 выходное напряжение f/вых является линейной функцией сопротивления R5:

[/вых - Ri

0+a)Au(s)UBbix

(6.99)

l+a+Au(s) Rs Rs

Поэтому схему Хауленда можно применять для построения омметров с линейной шкалой и постоянным значением тока в измеряемой цепи.

Центральное звено схемы Хауленда - управляемый током источник тока, схема которого показана на рис. 6.19а;. Если источник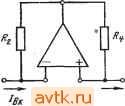

Ifft/x Zj \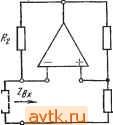

Rf. \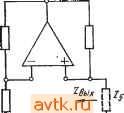

Рис. 6.il9. ,У1пра(ви1 амые .током исшочшки тока, осиюве имвйртирующих пре-О1фаао1вателе1й 10три1цател1ьного иммтанса

нагружен на сопротивление Z5, как показано на рис. 6.196, то выходной ток, определяемый выражением (6.95), и входное сопротивление будут соответственно равны

RjAu. (s) /вх Au{s) J

Ri l+Au(s)

7-1? Rj + Zbll-Aujs)] 7 Ri Au(s)-

Rin+Au(s)]Z

Ri Au(s) + \

(6.100) (6.101)

Если на входе источника включено сопротивление Z\, как показано на рис. 6.19в, то вычисленное по (6.97) выходное сопротивление

z=R-L±ALm±3 z,. (6.102)

Z + RAl-Au{s)] i?, Л„(5)-1

Из выражений (6.101) и (6.102) следует, что при Л (5)>1 схема работает как инвертирующий по току преобразователь отрицательного иммитанса, в котором полные сопротивления со стороны

входных и выходных зажимов преобразуются с коэффициентом -R2/R4 или -Ri/Rz- Схема сохраняет устойчивость при условии

ZjRZR. (6.103)

6.7. Интеграторы

Если внешние полные сопротивления, подключенные к идеальному инвертирующему ОУ, таковы, что Zi = Ri и Z2=l/sC2, то схема представляет собой идеальный интегратор (рис. 6.20а). Для идеальных интеграторов выходное напряжение пропорционально интегралу, взятому по времени от входного напряжения

/выг=- i t/вхЛ+г/о.

(6.104)

где Т'и=/?12 - постоянная времени интегратора, [/о - начальное напряжение, определяемое начальными условиями. Для анализа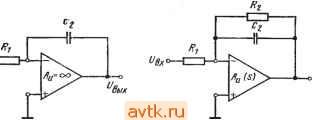

Рис. 6.20. И|Д1баишый (а) и реальный (б) MHTferpaTopbi иа юснове ОУ

реальных интеграторов, в которых ОУ имеет конечный коэффициент усиления, можно использовать следующее выражение:

(S) = - Л„ {S) ZAZ+Z, + A, (S) ZJ.

(6.105)

Если Zi = R\ и конденсатор не является идеальным, то

Z = R{\-\-sRd), (6.106)

где R2 - результирующее сопротивление утечки, включенное параллельно с интегрирующим конденсатором (рис. 6.206). Таким образом, при t/o=0 получим соотношение

которое можно переписать

(6.107)

t/вых =

и

. Au(s)

sRiC2ll+Au(s)]0 + ysRC2)i 233

(6.108)

Если Au{s)=AuJ{i+s/ao) и Ли >1, то

t/выг -

sTj l + l/sTc l + l/s-4 rj 1

(6.109)

l+sO+sT)/Oo(i+sAu T)

где TiiRiCi; Tc=R2C2.

Выражение (6.109) представляет собой произведение четырех сомножителей. Первый сомножитель [/вых/[/вх=-I/sTh соответствует передаточной функции по напряжению идеального интегратора (рис. 6.21). Второй сомножитель учитывает погрешность, вно-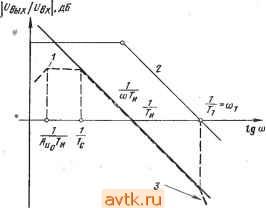

Рис. 6.21. Диаграмма Боде для реального интегратора: - низкочастотная погрешность, 2 -АЧХ усилителя, 3 - высокочастотная погрешность

симую токами утечки. Третий, называемый статической ошибкой, обусловлен конечным значением коэффициента усиления ОУ. И, наконец, четвертый сомножитель учитывает высокочастотные погрешности. Принимая mril и пользуясь подстановкой щАи, - =0)1, четвертый сомножитель можно переписать

{1 +s{l -f sr )/K(l -f s Л„ Ги)]}-1 (1 +s/(ui)-i.

Из анализа этих сомножителей и рис. 6.21 можно видеть, что интегратор на базе ОУ можно считать шрактичесии идеальным в интервале времени ГсТ^и^ь где Tc=R2C2 - постоянная времени утечки конденсатора, а 71= 1/mi-постоянная времени усилителя на частоте единичного коэффициента усиления.

Идеальная реакция на единичный скачок входного напряжения f/вх определяется выражением t/вых(0=-UJ/Tij. Низкочастотная (статическая) ошибка ухудшает эту реакцию и вызывает появление дополнительных членов

(6.110)

f/Bb:.(0=-f/Bx- il-e- -c)-U( 1-

Ти Ы \

Это, в свою очередь, вызывает появление относительной погрешности, которую можно записать

Аг/вых(№ых(0 -/27с, (6.111)

т. е. она линейно возрастает во времени (рис. 6.22а;).

Если интегрируюш,ий конденсатор является достаточно высококачественным элементом, а Аи имеет не очень большое значение, то Тс и Аи ,Ту1 могут оказаться величинами одного порядка. Тогда обе постоянные времени влияют на низкочастотную погрешность, в результате чего реакцию на ступенчатый сигнал и относительную погрешность можно записать

г/вы.(О = -, 1\ (е-- -е-/с)

Аг/вых(0 вых(0 -tmujH+ УТс)/2. (6.113)

Влияние высокочастотной погрешности приводит к изменению идеальной реакции на ступенчатый сигнал от г/вых(0=-Bxt/T до (рис. 6.226)

г/вь:х(0= - [t-TAl-e- )]. (6.114)

Если на вход интегратора подать синусоидальный сигнал частоты (О, то реакцию реального интегратора можно представить

г/вых( )=--- (6.115)

Реакция идеального интегратора была бы такой: [/вых(е)) = = -г/вх({о)/]соТ'и- Различие между этими реакциями можно охарактеризовать ошибками по амплитуде

А„((о) 0,5 (co/Mi) (6.116)

Фй ( ) = - arctg (M/cOi). (6.117)

Часть высокочастотной погрешности можно скомпенсировать посредством включения параллельно резистору Ri конденсатора Ci емкостью Ci = Th/Ri(1+ i7h) =1 ?1<й1- Теоретически высокочастотную погрешность можно уменьшить, увеличив иь Однако частотная характеристика используемого в интеграторе ОУ должна быть скорректирована из расчета получения Аи =1. Следовательно, данный метод практически может быть реализован только в случае применения высокочастотных усилителей, например Р.А715. Для ОУ класса цА748, LM101 и других с дифференциальными входными каскадами на комплементарных транзисторах, включенных по каскодной схеме, можно рекомендовать также частотно-зависимые шунтирующие цепи, при помощи которых сигнал проходит непосредственно на последующие каскады (рис. 6.23).