при помощи включенного по схеме ОК транзистора 7s с большим коэффициентом усиления.

Выходной каскад построен по схеме ОК на транзисторе Т/. Его эмиттерный ток определяется источником тока на транзисторе Ts. При больших уровнях выходного сигнала этот каскад работает в режиме класса АВ, причем максимум положительной и отрицательной полуволны выходного тока обеспечиваются соответственно транзисторами 7? и Г4.

Основной полюс передаточной функции, расположенный на частоте примерно 1 кГц, определяется емкостью интегрального конденсатора С. Благодаря большим коэффициентам усиления по току транзисторов Тъ и Тъ входной ток покоя усилителя LM3900 составляет 30 нА. Поэтому при малых токах управления сопротивление инвертирующего входа может быть довольно большим.

ГЛАВА 6

ПРИМЕНЕНИЕ ИНТЕГРАЛЬНЫХ ОНЕРАЦИОННЫХ УСИЛИТЕЛЕЙ

Будучи пригодными для использования как в линейных, так и в нелинейных системах, интегральные ОУ являются наиболее универсальными функциональными узлами в современных элект-роннных устройствах. .Поскольку их свойства весьма близки к идеальным, основное содержание процесса проектирования устройств на базе ОУ заключается в выборе цепи обратной связи,-наиболее приемлемой для решения поставленной задачи. Возможности построения внешних цепей обратной связи для операционных усилителей практически не ограничены, поэтому рекомендации по применению ОУ нельзя свести к описанию набора стандартных схем. В связи с этим ограничимся рассмотрением наиболее характерных случаев применения ОУ.

Более или менее жесткие требования, предъявляемые к разрабатываемому устройству, не позволяют считать ОУ идеальным. Другими словами, в процессе разработки следует учитывать эффекты, обусловленные нелинейностью элементов. В общем случае процесс проектирования содержит следующие этапы:

а) Расчет цепи обратной связи, обеспечивающей требуемые параметры сопряжения и передаточную функцию. Как упоминалось, одинаковые параметры можно обеспечить при использовании различных цепей. Следовательно, смысл этого этапа заключается в выборе цепи обратной связи, оптимальной с точки зрения обеспечения таких параметров, как смещение, дрейф, чувствительность и т. д.

б) Выбор типа усилителя, наиболее подходящего для решения поставленной задачи. Поскольку он базируется на технических

xapaihfipHCTHKax, то до начала расчета следует определить кри-териал.1е параметры устройства, в целом, совместимые с тех-ническиш! характеристиками. Поскольку в каталогах обычно приводятся только основные параметры, желательно знать также и принципиалы^ую схему ОУ.

в) Расчет цепей коррекции в соответствии с характеристиками ц,епи обратной язи, частотной характеристикой, допустимыми частотными иокажециями и особенностями управления.

г) Выбор оптимальных щепей смещения с учетом параметров смещения и дрейфа допустимых значений полных сопротивлений, конфигураций устройства и его элементов, выбранных на предыдущих этапах. \

Поскольку между \тими этапами существует взаимная связь, нахождение оптимального решения обычно требует применения итеративной процедуры. В инженерной практике принято начинать с расчета цепи обратной связи, считая ОУ идеальным; затем выбрать оптимальный с экономической и технической точек зрения тип ОУ; наконец; рассчитать цепи коррекции и смещения.

6.1. Инвертирующий усилитель с обратной связью

Значения сопротивлений и параметры передаточной функции инвертирующих усилителей с обратной связью, можно определить при помощи эквивалентной схемы, приведенной на рис. 6.1. Здесь Аи (s) - зависящий от частоты коэффициент усиления в режиме холостого хода; Zi - последовательное полное сопротивление на входе, включающее внутреннее сопротивление источника сигнала;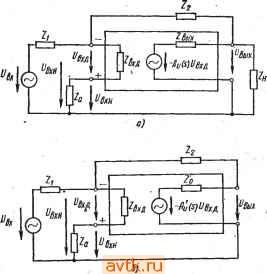

Рж. €.1. Эквивалениные схемы инвертадующего ОУ с офа-гаой связью .

- полное сопротивление обратной связи; Za - полное сопротивление, предназначенное для компенсации входного тока покоя.

Коэффициент усиления по напряжению можно рассяитать в два приема: сначала определить f/вх и в зависимости от [/вх, а затем рассчитать t/вых и, следовательно, коэффициент усиления по напряжению. Для простоты полное сопротивление нагрузки Zh можно объединить с полным выходным сопротивлением вых. Тогда 2вых=2н2вых/(2н-Ь2вых) и соответствующее напряжение эквивалентного генератора запишется UBuyi=-iAu{.s)l}y,sZ\ili7\i+

в модифицированной эквивалентной схеме, показанной на рис. 6.16 сопротивления Z\, (Zxn+Za) и (г+вых) образуют звезду. Напряжение в узловой точке

у (ВХ J-\- Zg) (Z2 -f- Zjibix) fJtiX + Zi (2bx Д + Zg) t/вЫХ (6 1)

(Zbx д + Zg) (Z2 + Zbix) + Zi (Zbx д + 2a + b + вых)

Поскольку

С/вхд = С/вхи-г/вхн = /,х„2вхд/(2вхд+г„) = -t/Bb,xM (s), (6.2)

Ц = {/ * (bx д b a) (Z2 -\- вых)

iBX r+Zg) (2а+2вь1х)+1 (Zbx r+ Zg + Z Zpbix) +

(6.3)

+ Au(s)ZiZbxji Подобным образом

вых ~ ( ВЫХ Bx и + 2 вых)/(2 Ь вых)

(6.4)

и, так как

1/вых= - (S) Ubx= -Л )/вхи^хд/(2вхд + 2 ), (6.5)

/вых = /вхХ

- Л'ц (s) Zbx д + 2вых (вх д ~Ь а)

(Zbx д + Zg) (Za + Zbmx) + (Zx д + 2 Z + Zix) +

- . (6.6)

+ Au(s)ZZbxji

Подставляя исходное выражение Au{s)ZH/{Zii+ZBMx) для .Au{s) в выражение (6.6), получим коэффициент усиления по напряжению усилителя с обратной связью

, , - Аи Zg Z Zbx д + вых Z (Zbx д ~Ь о)

~ (Zj + г^ых) [(Zbx д + Za) (Zg + Zbix) + Z, (Zpx д + Z r

+ Zg -I- г'вых)] + Аи (s) Zi Zj Zbx д

С учетом реальных соотношений сопротивлений это сложное выражение можно значительно упростить. Например, можно считать, что полное выходное сопротивление операционных усилите-

лей велико. Следовательно, 2вых всегда значительно меньше, чем Аи\Н,2 и вторым членом в числителе выражения (6.7) можно пренебречь. Тогда

J. , Ли (s) Zsx д

(fj + вых) И^вх R-\-Za) (Z2-\-Zbux) + Zi (Zbx д+а +

(6.8)

-IZa + Zbbix)] + Аи (s) A Z Zbx д

Физически такоё\упрощение означает, что составляющая сигнала прямой передачи по цепи обратной связи не учитывается. Поскольку возникаюгДая при этом ошибка ничтожно мала, выражение (6.8) можно считать точным.

Если Z2 значительно больше 2вых, выражение (6.8) можно переписать

4oc(s)~

Au(s)Z2ZZBxn

~ + вь1х) IZ2 (2вх д + Za)+Zi (Zbx R+Za + Z)] + Аи (s) ZZbx д ~

I I 1 Zi-f-Zbxд4 Zq-f-I] -

Zi L u(s) Zi Zbxj(

-I 7

Zh + Zsbix

(s)P(s)B(s)/(s)

(6.9)

где

AAs){s)Bis)K{s)T{s) (6.10)

- коэффициент усиления петли.

В вышеприведенном выражении Au{s), p(s), B{s) и K{s) соответственно означают коэффициент усиления по напряжению ненагруженного усилителя с разомкнутой обратной связью, коэффициент обратной связи и отношения, учитывающие конечные значения входного и выходного полных сопротивлений; B{s) и /C(s) определяются выражениями

fi(s) = -Bx /(2BXM + 2 + 2iZ2), (6.11)

K{s) = Z/{Z + Zb,ix). (6.12)

Дальнейшее упрощение возможно при условии ZbuxCZh и .Zbxa>(Z2+Zi). Тогда

Zi + Z2 + Au(s)Z

= --!-. (6.13)

Zi l--(Zi + Z2) lu (s)Zi

Если-Лг1(5) можно считать очень большим, то допустимо i+Z2)Mn(s)Zi<l и Аи чае идеального усилителя.

<Zi-t-Z2)/i4w(s)Zi<l и Аи (s)-Z2/Z1, что справедливо в слу-

Полное выходное сопротивление можно найти, зная коэффициент усиления петли. Из выражения (6.8) имеем .

° (Z + 2вь,х) [(Zbx к + ZJ (Z2+Zb x)+Zi (Zbx д+а++г'вых)]

(6.14)

Допущение Zh = oo дает . /

Гн ,(5)=-- ()1вхд-;- (6.15)

(Zbx д + (Z,+ZBbix)+Zi (Zx a+Z+Z+Zbhi)

При отрицательной обратной связи по напряжению'полное выходное сопротивление усилителя с обратцой связью Zbuxoc в [1-Ь7ноо(5)] раз меньще полного выходного сопротивления Zbux усилителя с разомкнутой обратной связью, т. е.

(Zbx д + Zg) (Zg + Zbix) + Z (Zx д + Z + Zg + вых)

(Zbx д + Za) (Zg + Zbhx) + Zi (Zbx д + Zq + Zg + Zbux) f Au (s) Zj Zbx д

(6.16)

При (s) Г двумя первыми членами в выражении (6.16) можно пренебречь, тогда

7 7 (Zbx д + Zg) (Zg + ZBbix) + Z (Zpx д + Zq + Zg -- Zbux)

вых ос - вых 2 i \ 7 7

(s) 1 bx д

(6.17)

Если можно допустить, что вхд^г^вых и ZbxZo, то

вых ос вых (Z,+Z2)M (s)i- (6.18)

Пусть Zo означает полное сопротивление ветви, проходящей от точки виртуальной земли через вход усилителя. Zo можно определить как полное входное сопротивление усилителя с параллельной обратной связью, состоящее из полного входного сопротивления усилителя без обратной связи и пересчитанного с учетом влияния обратной связи сопротивления Z2: Zo=ZBXfl+Za и Z o=Z2/(l +

+ ?rco(S)).

В последнем выражении

гр / ч (s) Z Zbx д ,g

~ (Z + Zbbix) (Zbx д + Z -f Zg+Zb x)

что следует из выражения (6.14) при условии Zi=oo. Теперь полное сопротивление в точке виртуальной земли можно записать в следующем виде:

Z,==Z,\\Z\

Z2(Zвxд + Zc)(г„ + гвыx)(Zвxд-Za-гa + г'выx)

(Zbx д + Z + Zg) (Z + 2вых) (Zbx д Н- Z -- -f Zsbix) + An (s) (Zjx д +

i ЕсЛЙч ZauxVlAuis) таковы, что Zh >Zbhx и Auis){ZaxR+

-t-Zo)ZBx>C (bxfl+Zo+Zz), TO справедливо соотношение

\ Zo Z,(Zв,д+Z + Z2)/Л„(s)Zз,д. (6.21)

Если полнО^ входное сопротивление очень велико, т. е. Zbxr : (Z2+Za), то В}>1ражение (6.21) упрощается и приводится к виду

Zo M (s). (6.22) Jr.

Общее полное входное сопротивление г усилителя с обратной связью представляет собой сумму Zq и последовательно включен- и^, o-i

НРГО Z]!

2вх ОС-l-Zo Zi-bZ,M (s). (6.23)

Небольшое значение полного сопротивления Zo характерно для всех инвертирующих усилителей с обратной связью. Если P e. 6.2. Инвйртирую-

считать точку виртуальной земли входом суммирующий j 1 > о усилитель с обратной

усилителя, то получается очень близкий к связью

идеальному управляемый током источник

напряжения, в котором входное и выходное полное сопротивления очень малы, а полное сопротивление прямой передачи определяется выражением

Zt = г/вых/4х -{Аи ( )/[ 1 + А^ (S)]} Zg -Z. (6.24)

Такие источники весьма удобно применять в различных линейных и нелинейных устройствах. Наиболее широко они используются для суммирования с различными весовыми коэффициентами. Принципиальная схема соответствующего устройства показана на рис. 6.2. На основе метода узловых напряжений для инвертирующего входа можно записать: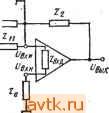

вых--

-2 /

\i=l

I L

вхд У 1

(6.25)

i + /f, L+ L+ L.y .

(6.26)

При выводе этих соотношений было принято, что Zbx a>Za и Zo~0. Если Auis) очень велик, то

/в-ых-- (627)

Из выражения (6.27) можно видеть, что выходное напряжение является взвешенной суммой входных напряжений.

6.2. Неинвертирующий усилитель с обратной связью

Значения сопротивлений и параметры передаточной функции неинвертирующего усилителя с обратной связью можно получить

при помощи эквивалентной схемы, показанной на рис. 6.3. Пользуясь методом, который был использован в § 6.1, получим

Лос( )= --

+ Zbix) [(Zbx д+Zr) (Z2-)-ZBbix)+ +л (Zbx д + Zr + Zg + Zbbix)] + (s) Zj Zj Zbx д

. (6.28)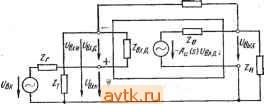

Р.ИС. 6.3. Эквивалеятная схема меишертирующего ОУ с обратной связью

Если Z2>ZBbix, то

Ли (s) Zbx л Zh (Zi + Zg)

(Zh + Zbux) [Zg (Zbx д + Z) + Z (Zbx д + Zr + Zg)] + Л„ (s) 2 Zbx д

Zi + Z, Zj

1 ) 1 Zi + Zg ZB + Z + ZiZg H + Bbix

u(s) Z, + Zg Zi

=-bx д 1

(6.29)

H (s)P(s)B(s)/C(s)J

При ZBbix<ZH и ZBXflXZa + Zr) выражение (6.29) можно упростить

Аиос ()=к (S) (Zi+Z,)/lZ,+Z,+AAs) Z] =

= (Zi+ZJ

Z1+Z2

(6.30>

(s)ZiJ

Если коэффициент усиления по напряжению очень велик, то (Z, + Z,yA, is)С 1 и A{s) {Z+ZyZ.

При Ubx = 0 усилители, показанные на рис. 6.1, 6.3, идентичны. Исходя из этого, полное выходное сопротивление можно получить путем формальной замены Za на Zr в выражении (6.14)

7 /7 (Zbx д + Zr) (Zg -- 2вых) + Z (Zbx д + Zr + Zg -- Zbbix)

вых ОС ых iiniT;;;

(6.31)

Если Лп(5)>1, ZBbix<Z2 и ZBxrXZ2+Zr), то справедливо

ВЫХ ОС

2Bbix(2l + 22)M.(s)Zi

(6.32)

Вследствие наличия последовательной обратной связи полное входное сопротивление усилителя с замкнутой обратной связью в

[1+7*(8)] раз больше полного входного сотротйвления усилителя с разомкнутой обратной связью. Tro(s) представляет собой коэффициент усиления петли, измеренный при Zr=0. Из выражения (6.28) имеем

=-- >н^в.д - - g33

(Zj -h Zjjbix) [ZbX Д (2 -Н Z jjbix) -}- Zj (Zjjx Д^-Z2+Zвыx)]

Для полного входного сопротивления разомкнутого усилителя со стороны неинвертируюшего входа можно записать

Zbx - вх д + l JKa + вых) =

вх Д (2 + Zsbix) + Zi (Zbx 71 + 2 + Zbhx

1 + 2 + ZiblX

откуда -

вхос = 2вх(1+По(5)) = 2 i 2 (H 4 вых) + Z Zbhx + (s) Zbx л Z (6 34)

~ (Zi-f-Z2)(Zj-t-ZBbix) + ZHZBbix

Если выходное сопротивление и коэффициент усиления по напряжению таковы, что 2вых С2н и (s)Zbx д>22, то допустимо

2вх ос 2вх д [ 1 + 2l л, {S)/(Z + Zj)]

2bx oc(s)2i/(2i + 22). . {6.35>

Рассмотренное полное входное сопротивление может быть очень большим и даже превосходить полное входное сопротивление для синфазной составляюшей

Zbx с) которое не учитывалось при выводе вышеприведенных выражений. Следовательно, в случае большого коэффициента усиления петли входным сопротивлением Zbx с пренебречь нельзя. Как было показано (см. § 4.4), Zbx с является результирующим двух составляющих: Zbxci и Zbx с 2- Если усилитель симметричен, то Zbxc1Zbxc2 и Zbx c = Zbx с i/2.

Поскольку единственным фактором, влияющим на полное входное сопротивление неинвертирующего усилителя, является сопротивление Zbx с 2, которое связано с неинвертирующим входом, то общее входное сопротивление определяется

вх ос ~ 2 Zgx с II вх д Ац {s)Z/{Z + Z). (6.36)

В широко применяемых интегральных ОУ полное входное сопротивление для синфазной составляющей больше, чем для дифференциальной на 2-=-3 порядка. Типичные входные сопротивления для синфа.зной составляющей характеризуются параллельно включенными сопротивлением 10-=-500 МОм и емкостью 1-=-5 пФ. Чтобы снизить влияние дрейфа, составляющая по постоянному току сопротивления Zr обычно выбирается меньше омической составляющей сопротивления Zbx л (для простых дифференциальных каскадов входной ток покоя и дифференциальное входное сопротивление взаимосвязаны). Как правило, .очень большое входное

сопротивление, обеспечиваемое при использовании такого вида обратной связи, не может быть полностью реализовано.

Особой разновидностью неинвертирующего усилителя с обрат- ной связью является усилитель-повторитель. Он представляет собой усилитель с единичным коэффициентом усиления и последовательной обратной связью, в котором Z2=0 и Zi = cxd (рис. 6.4а).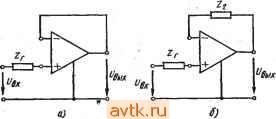

Рас. 6.4. Усилители-повторители с единичным коэффициентом усиления

Для обеспечения компенсации смещения, обусловленного входным током покоя, сопротивления по постоянному току со стороны каждого входа усилителя должны быть одинаковы. Это является причиной того, ча-о условие Z2=0 заменяется условием Z2a=o=-=Zia =0, как показано на рис. 6.46.

На основании формулы (6.28) коэффициент усиления по напряжению усилителя с замкнутой обратной связью можно записать

Ли (s) Zbx д

-. (6.37)

(Zh-j-Zbbix) (Zbx fl+Zr-bZ2-t-ZBbix)-i-u(s)ZH Zbx д

Если коэффициент усиления усилителя с разомкнутой обратной связью Au{s) велик, а выходное сопротивление Zbhx мало, справедливо соотнощение

4ос() (s)2Bxfl/[ZBx + Zr + Z, + (s)ZBx l. (6.38)

при Zвxд> (Zr-bZ2) коэффициент усиления Auis) можно определить приближенно

AuoMAAs)/{l + AAs)). (6.39)

Из выражения (6.16) выходное сопротивление при наличии обратной связи находится

Zbx л + Zr -Ь Zg -}- Zbbix

вых

Zbx д -f- Zr -f- Za -}- Zвыx + ( ) Zbx д

Если Au{s) и Zbx я достаточно велики, то

вых ос 2вых/[Ц-4( )1-

(6.40)

(6.41)

Для входного сопротивления усилителя с замкнутой обратной связью справедливо соотношение

вх ОС 2 вх с II [вх д ~1~ 2 вых ~1~

-4(s)Zв^дZн/(Zн^-Zвв:x)l.

(6.42)

Если Au{s) велик и 2вхд> (22+2вых), то сопротивление Zbxoc весьма велико и составляет

бх ос 2.2вхс1[2вх (И-Л(8))1- (6.43)

6.3. Источники погрешностей ОУ с обратной связью

Реальные усилители являются лишь некоторыми приближениями к идеальным. В связи с тем, что значения коэффициента усиления по напряжению усилителя с разомкнутой обратной связью Au{s), его полное входное и выходное сопротивления конечны, фактическое значение коэффициента усиления всегда отличается от идеального. Это можно учесть путем введения поправок в соответствующие выражения для коэффициентов усиления.

Для инвертирующих усилителей с обратной связью выражение (6.9) можно переписать

4оси ()=-

где rn(s) - коэффициент усиления петли, определяемый выражением (6.10).

Для неинвертирующих-усилителей с обратной связью выражение (6.29) также можно представить в другом виде:

А (Л - 1 + 2 Гп (S)

В обоих случаях первый член определяет идеальный коэффициент усиления, а второй - поправку.

За исключением единственного различия, заключающегося в замене Zo на Zr, выражения для коэффициентов усиления петли инвертирующего и неинвертируюшего усилителей одинаковы. Поэтому для определения относительных погрешностей коэффициентов усиления можно пользоваться одной и той же поправочной функцией

h{s)\/{l+TAs)). (6.46)

Конечный коэффициент усиления усилителя с разомкнутой обратной связью. Бели коэффициент усиления Au{s) имеет конечное значение, а Zbxaoo и Zbhx=0, то Tn{s)=Au{s){s) и

.ч 1 1 t

1-ЬГп(8) l-- (s)P(s) l + Au(s)Zi/(Zi + Z2) .