Сопряжете цифрошх и щалоговых сигналов 105

будет меняться в соответствии с условием равенства общего количества красных и синих шаров.

Представление о том, каким образом это происходит, можно получить, рассматривая случайные блуждания. Если предположить, что единственное неслучайное свойство регистровой последовательности состоит в том, что число единиц точно равно числу нулей (пренебрегая дополнительной 1), можно показать, что при одинаковом и равном К/2 общем числе единиц и нулей после г испытаний среднее смещение от начальной точки в результате случайных блужданий будет равно

X = [r(/C-r)/(/C-l)F

При полностью случайных блужданиях X равно г'*, а коэффициент (К-г)1{К-1) описывает эффект конечного содержимого урны. Поскольку г<К, случайность блужданий лишь незначительно уменьшается по сравнению с идеальным случаем (бесконечное содержимое урны), и рассматриваемые псевдослучайные последовательности вполне соответствуют этой модели.

Авторы рассматривали несколько тысяч случайных блужданий, вызванных ПСДП, каждое из которых имело в длину несколько тысяч шагов, и установили, что случайность, измеренная в соответствии с указанным простым критерием, является практически идеальной.

Конечно, тот факт, что генераторы ПСДП удовлетворяют этой простой проверке, не гарантирует того, что они будут удовлетворять и другим, более сложным критериям случайности, например при измерении корреляции более высокого порядка. Эти корреляционные зависимости также оказывают влияние на характеристики аналогового шума, полученного из такой последовательности путем фильтрации. Хотя амплитуда такого шума имеет гауссово распределение, здесь могут возникнуть корреляции амплитуды высоких порядков, не свойствен- ные действительно случайным шумам. По этому случаю следует отметить, что качество шума может быть улучшено за счет увеличения количества выходов для подключения ОС (предпочтительное число равно т/2). Последовательный входной сигнал формируется в этом случае при помощи паритетного дерева.

Разработчикам генераторов шума следует знать о существовании КМОП-регистра переменной длины (от 1 до 64 разрядов) типа 4557. Для того чтобы получить п точек подключенвгя ОС, его, разумеется, Чужно использовать в сочетании с регистром, имеющим параллельные выходы, как, например, 4015 или 74С164.

f В разд. 7.19 обсуждался вопрос генерации шумов и рассматривался генератор розового шума, который использует интегральный регистр 1!Ш?С ймальмой длины типа ММ5ё37.

9.40. Цифровые фильтры

Последний пример затронул интересную тем^г, связанную с цифровой фильтрацией, а именно вопрос о формировании аналогового НЧ-

сигнала путем взвешенного суммирования 32 значений псевдослучайной последовательности, каждое из которых соответствует уровню напряжения О или 4-12 В. На вход этого фильтра поступает сигнал, который может иметь только два уровня напряжения. Вообще, то же самое можно сделать и при использовании на входе аналогового сигнала, если сформировать взвешенную сумму его значений (лгё), взятых через равные интервалы времени:

k=-a>

Здесь xi представляют собой дискретные отсчеты входного сигнала, hh - весовые коэффициенты, а t/t - выходной сигнал фильтра. В реальных условиях цифровой фильтр суммирует лишь конечное число значений входного сигнала, как это, например, имело место в рассмотренной схеме генератора помех, где использовались 32 члена. Каким образом выполняется такая операция, в схематической форме показано иа рис. 9.74.

Направление двикенйя данных-*~

-будущее

Настоящее Прашпое

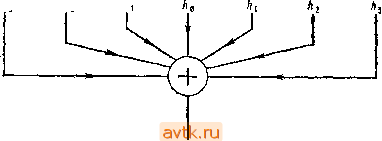y, (от!рильтрованный выход j Рис, 9.74. Нерекурсивный цифровой фильтр.

Заметим одно интересное свойство этого фильтра: его можно сделать симметричным во времени, т. е. усредняющим в выходной точке, взятой в ачестве текущего момента, как прошлую, так и будущую историю . Реальные аналоговые фильтры могут, разумеется, лишь смотреть в прошлое и соответствуют цифровому фильтру, у которого весовые коэффициенты имеют ненулевые значения только при

Частотная характеристика симметричного фильтра.

Можно показать, что частотная характеристика симметричного фильтра {hk=hh) будет определяться следующим соотношением]

Я(/) = / + 2 2 hf,Q0s2nkft

ore*

где - интервал между двумя отсчетами. Нетрудно заметить, что ftft представляют собой коэффициенты разложения в ряд Фурье для

требуемой частотной характеристики. Это объясняет, почему в случае рассмотренной схемы генератора шума весовые коэффициенты были выбраны пропорциональными (sin х)/х: они представляют собой коэффициенты Фурье для идеального заграждающего НЧ-фильтра. Фазовый сдвиг такого симметричного фильтра на любой частоте будет равен либо нулю, либо 180 .

Рекурсивные фильтры. Можно создать интересный класс цифровых фильтров, если к поступающему на вход фильтра внешнему сигналу добавить свой собственный выходной сигнал. Таким образом мы получим фильтр с обратной связью. Фильтр подобного типа называется рекурсивным цифровым фильтром в отличие от рассмотренного выше нерекурсивного фильтра. Можно, например, сформировать выходной сигнал в соответствии со следующим соотношением:

Оно представляет собой характеристику низкочастотного фильтра, эквивалентного простейшему /?С-фильтру при

где отс - интервал между последовательными отсчетами входного сигнала. Конечно, эта ситуация в силу дискретного характера отсчетов не идентична аналоговому НЧ-фильтру, воспринимающему аналоговый сигнал.

Пример НЧ-фильтра. В качестве числового примера предположим, что требуется отфильтровать ряд числовых значений, обеспечивая затухание 3 дБ на частоте/-здб=1/20 /отс Выбранная постоянная времени соответствует, таким образом, 20 последовательным отсчетам. В этом случае Л =0,95123, а выходной сигнал будет определяться соотношением г/г=0,95123 /i i4-0,04877 Xi. При увеличении постоянной времени по сравнению с интервалом отсчета эта характеристика приближается к характеристике реального НЧ-фильтра.

Такие фильтры используются для обработки данных, которые уже представлены в виде цифровых отсчетов, наприйер массива информации в ЭВМ. В этом случае рекурсивная фильтрация будет Представлять собой обычный шаг арифметической обработки единицы информации. Программа НЧ-фильтра на языке 4Н)ртран будет выглядеть следующим образом:

A = EXP(-TS/TC) В = 1.~А ЕЮ 101=2, N 10 Х(1) = А*Х(1 -1)+В*Х(1)

где X означает массив данных, TS - интервал между двумя отсчетами (т. е. TS=l oTc) ТС - выбранная постоянная времени. В идеальном случае TCTS. Эта маленькая программа производит фильтрацию

Рис 9 75 Рекурсивный цифровой фильтр.

месте, т. е. заменяет исходные данные их отфильтрованным значением. Отфильтрованные данные можно, конечно, поместить и в отдельный массив.

Коммутационный НЧ-фильтр. На рис. 9.75 показано, как можно построить такой же фильтр при помощи аппаратных средств. Р-, V Ключи St и Sa, выполнен-

J и U \ , полевых транзисто-

рах, коммутируются с некоторой тактовой частотой /отс, периодически заряжая конденсатор Ct до уровня входного напряжения и передавая затем его заряд конденсатору Cg. Если напряжение на Сг равно U, а напряжение на Ci равно Ui, то при подключении Ci к Сг напряжение на обоих конденсаторах будет определяться соотношением U = =(Cif/i+C2(/2)/(Ci-fC2), что эквивалентно рассмотренному выше рекурсивному НЧ-филътру при

у, = [С,КС + С,)] г/, , + [CJiC, + С,)] X,.

Приравнивая эти коэффициенты выбранному выше значению А, получим

/адБ = (1/2я)/о,е lg[(C,+C,)/C,].

Упражнение 9.6. Покажите, что этот результат правилен.

Рассмотренная схема фильтра применяется на практике и обладает удобным свойством электронной настройки по частоте/отс- В реальных схемах обычно используются КМОП-ключи, а емкость Ci берется много больше Са, поэтому сигнал управления ключами должен быть несимметричным и замыкать Si на более продолжительное время.

Приведенная схема представляет собой простой пример коммутационного фильтра, к которому относятся фильтры, построенные из набора коммутируемых конденсаторов. Они имеют периодическую частотную характеристику, что делает их удобными для использования в качестве гребенчатых и запирающих фильтров.

Для всех классических фильтров (Баттерворта, Чебышева и т. п ) можно построить их приближенные дискретные аналоги в форме НЧ, ВЧ, полосовых и заграждающих фильтров, как симметричных во времени, так и обладающих истинным временем запаздывания. Такие фильтры очень удобны при обработке квантованной цифровой информации и, безусловно, имеют большое будущее.

Формирование синусоидального сигнала цифровым способом. С нерекурсивной цифровой фильтрацией связан интересный способ получения синус9Идальн2):о сигнала путем взвешенного сумми-

Выход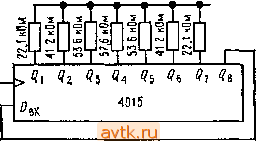

рования выходов счетчика Джонсона (или кольцевого счетчика). Как это делается, иллюстрирует схема на рис. 9.76, в которой использован 8-разрядный регистр сдвига с параллельными выходами типа 4015. Если на вход регистра подать проинвертиро-ванный выход последней ячейки, то получится счетчик Джонсона, который проходит через 16 состояний (в общем случае для -разрядного регистра сдвига число состояний равно 2п). Начиная с нулевого состояния, регистр слева направо заполняется единицами . После того как единицы будут записаны во все разряды, в регистр начнут записываться нули и т. д. Показанная схема позволяет получить 8-уровневую аппроксимацию с частотой, равной 1/16 /такт, и имеющую ненутс-

вой член искажения на 15 гармонике, имеющей затухание 24 дБ (считая резисторы идеальными).

1б таит

Г

Рис. 9 76. Цифровой генератор синусоидальных сигналов.

схемы, не требующие пояснений

9.41. Удачные схемы

На рис. 9.77 дано несколько примеров сопряжения логических и линейных устройств.

9.42. Негодные схемы

На рис. 9.78 приводятся грубые ошибки, часто совершаемые при сопряжении различных устройств. Попытайтесь для каждого случая выяснить, в чем состоит ошибка и как ее устранить.

дополнительные упражнения

(1) Постройте схему, и*<йицирующую кратковременное исчезновение напряжения питания (+5 В) Схема должна иметь кнопку СБРОС и светодиод ддя индикации НЕПРЕРЫВНОГО ПИТАНИЯ. Питание схемы должно производиться от источника +5 В.

(2) Почему нельзя построить ЦАП на 2п разрядов, суммируя выходы двух й-разрядных ЦАП по закону (BbIXi+BbIX2/2 )?

(3) Убедитесь в том, что максимальное значение сигнала на выходе генератора псевдослучайного шума на рнс. 9,73 действительно составляет =t:4,34 В,

(4) Для управления экспериментом используется программируемый калькулятор, к которому подключены различные исполнительные н измерительные устройства {рис. 9 79). Калькулятор дает приращения находящимся под его управлением переменным (например, длине волны излучения, поступающего от монохроматора) н обрабатывает соответствующие измерения (например, количество переданного света, скор-

УДАЧНЫЕ СХЕМЫ

IkOm

Логика ТТЛ

Логика МОП

а

(5) Лампа

д

-(высокий уровень, если ип<1/ы<1в)

Соленоид 15В,1А

Инберсные -j

БКОР.Ы

Входы выбора канала(ТТЛ) отпирающий вход(ттл)

Прямь1е ~г mm

10 nOm Ш кОм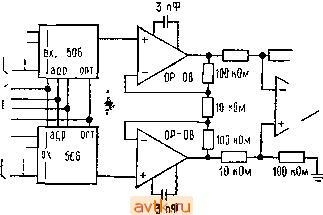

Выход

(Дисрф

коэфф чст-

Рис. 9.77.

а - преобразователь отрицательных уровней в уровни ТТЛ; б - управленне нагрузкой, подключенной на землю; в - амплитудный дискриминатор, г -= схема управления соленоидом;, d 8 канальный мультиплексор с дифференциальным входом. -

НЕГОДНЫЕ ШМЫ Л,0 кОм

ТТЛ ТТЛ

а

ТТЛ

к другим вентилям

выхоа

+15(или+5]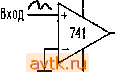

- -15(или земля)

е

Рис. 9 78-

-mm-j

Внутреннее сопро -

тивлени8 10 кОм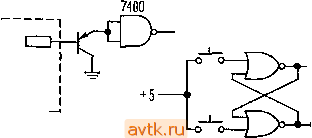

к дополнительным вкодзм)

+15 I

ТТЛ JU

а - формирователь задержанного фронта; б - индикатор логического состояния; в сопряжение элемента ТТЛ с высокоомным выходом (две неудачные схемы); г - повышение нагрузочной способности элемента ТТЛ с помощью повторителя, - проводное ИЛИ на вентилях с активной нагрузкой; е - счетчик пересечений нуля* Ж == RS триггер; з = соррягкение й§мента ТТЛ со схемами высоких уровней.

ректированное для известной чувствительности детектора). В результате образуются пары значений х, у. Задача состоит в том, чтобы построить схему, с помощью которой эти пары значений могли бы быть выведены на аналоговый самописец.

Калькулятор вводит каждую пару значений х, у виде двух 3-значных двоично-десятичных символов Для того чтобы сократить необходимое количество соединений, каждый раз передается одна цифра выводимого числа (битовый вывод - параллельный, символьный - последовательный) в сопровождении двух адресных разрядов. Импульс данные действительны сообщает о том, что данные и адрес выведены на ши-иу и могут быть восприняты. Потенциальный сигнал х'/у сообщает о том, какому числу принадлежит выводимый символ (л^ или у). Это показано на рис. 9 79.

Двоично-

десятичный символ

АдресД; символа

Q цифра X Ьцифрз vj

с уровнем ттл все данные Леи:твите;1ьны

координатный сзмопи сен

0Т-5в до+5 5

{уровень О В еыаоди! шт* сец уг середину бумаги;

Дешифрация адреса Символа:

Рис. 9.79.

Данные передаются в следующем порядке: ; с„(МЗЦ), . . .1с„(СЗЦ), у„(МЗЦ), у„(СЗЦ), поэтому известно, что законченная пара х, у будет получена после приема СЗЦ числа у (1=0, А^-\, х'/у=1). В этой точке нужно скорректировать цифры, которые воспринимает ваш ЦАП (не корректируйте их по одной каждый раз).

Используемым элементам не нужно присваивать номера конкретных ИМС Дайте им лишь общие обозначения, например £>-триггер, или дешифратор I-10 Не забудьте с помощью маленьких кружочков указать, где используются инверсные входы и выходы. Считайте, что в вашем распоряжении имеется ЦАП, который воспринимает три двончно-десятичных символа на входах, совместимые с уровнями ТТЛ, и обеспечивает выходной токовый сигнал, изменяющийся от О до 1 мА при изменении входного числа от ООО до 999. Паскольку^для двухкоординатного графопостроителя отклонение полной шкалы составляет 10 В, ток нужно будет преобразовать в напряжение. Введите дополнительное усложнение, считая, что выходной сигнал ЦАП может ме-нятьсн в пределах лишь 1 В

Глава 10 МИНИ-ЭВМ

мини-эвм, микро-эвм и микропроцессоры

Наличие сравнительно недорогих (5000 долл.) малых ЭВМ дало возможность управлять экспериментами и технологическими процессами, производить сбор данных и выполнять расчеты непосредственно под управлением вычислительной машины. Малые ЭВМ широко используются в лабораторных и промышленных установках, а поэтому знание их возможностей, языков программирования и интерфейсных требований становится неотъемлемой частью прикладной электроники.

Под термином мини-ЭВМ мы будем иметь в виду малую вычислительную машину, центральный процессор (ЦП) которой выполнен на ИМС средней и большой степени интеграции и занимает обычно одну или несколько больших плат. Что касается микро-ЭВМ, то она представляет собой вычислительную машину, у которой ЦП состоит из небольшого числа (часто только одной) ИМС большой степени интеграции (БИС). Сам кристалл (или набор кристаллов) ЦП носит название микропроцессора. Возможности мини-ЭВМ и микропроцессоров в значительной степени совпадают, хотя микропроцессоры, имеющие небольшое число кристаллов памяти и ввода/вывода, чаще всего используются в блоках управления технологическими процессами или измерительными приборами, в то время кас мини-ЭВМ обычно находят применение в тех случаях, когда необходимо иметь бэлее мощные вычислительные и периферийные возможности и высокое быстродействие. Микропроцессор в сочетании с несколькими стандартными блоками и постоянным запоминающим устройством (ПЗУ) способен заменить сложные логические схемы, содержащие вентили и триггеры, а также может выполнять функции аналого-цифрового преобразователя (АЦП). Все эти возможности следует рассматривать всякий раз, перед тем как приступить к работе над большим проектом. Микропроцессоры в сочетании с большим количеством блоков памяти и периферийных устройств образуют микровычислительные системы, которые благодаря своим возросшим возможностям стали составлять серьезную конкуренцию большим и мини-ЭВМ в сфере их традиционного применения - решения сложных расчетных задач. Действительно, слова мини-ЭВМ и микро-ЭВМ используются сейчас повсюду, причем в ряде случаев различия между ними определяются скорее физическими размерами ЭВМ или числом периферийных устройств, чем степенью интеграции, используемой в блоке ЦП.

В данной главе мы рассмотрим архитектуру, программирование и интерфейсы мини-ЭВМ и на простых практических примерах пока-

жем, как к ним подключаются периферийные устройства. Большинство введенных здесь понятий будут использоваться также и в следуюш^ей главе, в которой мы приступим к подробному обсуждению вопросов выбора и построения различных систем на базе микропроцессоров. Вообш^е говоря, что касается мини-ЭВМ (и до некоторой степени микро-ЭВМ), то построение собственно вычислительной машины (включаю-ш.ее в себя интегрирование памяти и системы управления вводом/выводом), а также разработка системного программного обеспечения и сервисных программ обычно осушествляются изготовителем. Пользователь же должен позаботиться только о сопряжении нестандартного оборудования и о составлении прикладных программ. В противоположность этому в системах со встроенным микропроцессором выбор типа памяти, внутрисистемных связей и программирования должен обычно выполняться разработчиком системы. Изготовители мини-ЭВМ обычно поставляют обширное системное и сервисное программное обеспечение в виде части законченной вычислительной системы (включаю-ш.ей периферийные устройства), в то время как изготовители микро-ЭВМ (т. е. изготовители полупроводников),как правило, видят свою основную задачу в разработке и сбыте кристаллов микропроцессора и сопутствующих блоков. В связи с этим в данной главе мы рассмотрим архитектуру и программные средства ЭВМ, останавливаясь более подробно на вопросах внутренних связей и сопряжения с внешними устройствами.

10.1. Архитектура ЭВМ

Хотя различные ЭВМ функционируют различным образом, суи;ест-вует обобщ.енная структура, типичная для большинства вычислительных машин, которая приводится на рис. 10.1. Рассмотрим этот рисунок слева направо.

Шина данных

Схема упоавлекия шт \

Регистры

стека

Счетчик

Магнитная или лояу лроводни новая fia мять с проиавопь-НОЙ выборкой

ПЗУ

Дисц и л

лента

□

Видеотермй лап

Печатаю-

щеечст-

роиство,

графоло-

c:poh:e;i(j

считыва

теяь и1 п

ЦАП

Цифровой ввод-

ОЫбОД

процесс жщтт и тп

Ориентированные на Ориентированные на об-арифмвтичЕские рабошц данных в реапь-- операций -нам масшта- . fe времени . -----Устраиства -

Рис, 10.1. Блок-схема лабораторной ЭВМ.

Центральный процессор. Блок центрального процессора (ЦП) представляет собой ядро вычислительной машины. В процессе вычис-