числа. Так как действующие напряжения и токи представляют собой реальные количественные величины, изменяющиеся во времени, следует вывести правило для перевода реальных количественных величин в комплексное представление и наоборот. Напомним еще раз, что мы имеем дело с частотой синусоидального колебания со, и сформулируем следующие правила:

1. Напряжение и ток представляются комплексными величинами и и I. Напряжение Uo со5(со/+ф) представляется комплексным числом

2. Для того чтобы получить выражение для действующего напряжения и тока, нужно умножить соответствующие комплексные представления на е^ и выделить действительнук) часть. Это записывается следующим образом: U{t)=Re{\ie> ), /(O = Re(Ie®0- Иначе говоря,

Напряжение в схеме Комплексное пред-

как функция времени ставление

(; соз(а)/ + ф) ll,eif = aib.

умножить на е' и взять действительную часть

(В электронике символ / используется вместо принятого в алгебре для комплексной переменной символа i, с тем чтобы избежать путаницы с током, который также обозначают символом t). Итак, в общем случае действующие напряжения и токи определяются следующим образом:

и (/) = Re (Ue 0 = Re (U) cos lo - Im (U) sin со/, / {t) = Re (leO = Re (I) cos со/ - Im (I) sin со/.

Например, комплексному напряжению U=5/ соответствует реальное напряжение

(/(/) = Rc[5/ cos а)/+5/(/) sin со/]=5 sin со/.

Реактивное сопротивление конденсаторов и индуктивностей. Принятое соглашение позволяет применять закон Ома для схем, содержащих как резисторы, так и конденсаторы и индуктивности. Оп-)еделим реактивное сопротивление конденсатора и индуктивности.

известно, что (/(/)=Re(t/oe®0- Так как в случае конденсатора справедливо выражение I=C{dU/dt), получим

/(/) = - и,Са sino)/ = Re [(/ое 7(- wQ] Т. е. для конденсатора

Xc=-iaCi

52 Гмва 1 .

Хс- это реактивное сопротивление конденсатора на частоте со. Конденсатор емкостью 1 мкФ, например, имеет реактивное сопротивление -2653/ Ом иа частоте 60 Гц и -0,16/ Ом на частоте 1 МГц. Для постоянного тока реактивное сопротивление равно бесконечности.

Аналогичные рассуждения для индуктивности дают следующий результат:

Xi.=/coL.

Схема, содержащая только конденсаторы и индуктивности, всегда обладает мнимым импедансо.м; это значит, что напряжение и ток всегда сдвинуты по фазе друг относительно друга на 90° - схема абсолютно реактивна. Если в схеме присутствуют резисторы, то импеданс имеет и действительную часть. Под реактивным сопротивлением подразумевается при этом только мнимая часть импеданса.

Обобщенный закон Ома. Соглашения, принятые для представления напряжений и токов, позволяют записать закон Ома в следующей простой форме:

I = U/Z, U = IZ,

означающей, что напряжение U, приложенное к схеме с импедансом Z, порождает ток I. Импеданс последовательно и параллельно соединенных элементов определяется по тем же правилам, что и сопротивление последовательно и параллельно соединенных резисторов:

Z = Zj -f Zj -f 2з -f ... (для последовательного соединения),

\lz\lZi-\-\iz -f-- параллельного соединения).

И в заключение приведем формулы для определения импеданса резисторов, конденсаторов и индуктивностей;

R = R (резистор),

Zc = - соС (конденсатор), Zi = /aC (индуктивность).

Полученные зависи.мости позволяют анализировать любые схемы переменного тока с помощью методов, принятых для схем постоянного тока, а именно с помощью закона О.ма и фор.мул для последовательного и параллельного соединения элементов. Результаты, которые мы получили при анализе таких схем, как, напри.мер, делитель напряжения, сохраняют почти такой же вид. Так же как и для схе.м постоянного тока, для сложных разветвленных схе.м переменного тока справедливы законы Кирхгофа; отличие состоит в том, что в.место токов / и напряжений U здесь следует использовать их комплексные представления: сумма падений напряжения (ко.мплексного) в замкнуто.м контуре равна нулю; сумма токов (комплексных), втекающих в узел, равна сумме токов (комплексных), вытекающих из него. Из последнего правила, как и в случае с цепями постоянного тока, вытекает, что ток (комплексный) в последовательной цепи всюду одинаков,

Упражнение 1.16. Используя формулы для импеданса параллельного и последовательного соединения элементов, выведите формулы (разд. 1.12) для емкости двух конденсаторов, соединенных (а) параллельно, (б) последовательно. Подсказка: допустим, что в каждом случае конденсаторы имеют емкость С( и Cj. Запишите выражение для импеданса параллельно и последовательно соединенных элементов и приравняйте его импедансу конденсатора с емкостью С. Найдите С.

Попробуем воспользоваться рекомендованным методом для анализа простейшей цепи переменного тока, которая состоит из конденсатора, к которому приложено напряжение переменного тока. После этого кратко остановимся на вопросе о мощности в реактивных схемах (это будет последний кирпич в фундаменте наших знаний) и рассмотрим простую, но очень полезную схему /?С-фильтра.

Представим себе, что к силовой сети с напряжением ПО В (эффективное значение) и частотой 60 Гц подключен конденсатор емкостью 1 мкФ. Какой ток протекает при этом через конденсатор? Воспользуемся обобщенным законом Ома: Z=- соС. Следовательно, ток можно определить следующим образом: I = U/Z. Фаза напряжения произвольна, допустим и=Л, т.е. (7 (/)=Л cos со/, где амплитуда Л = 110К2л 156В, тогда 1=/соСЛя5:;0,059 sinco/. Искомый ток имеет амплитуду 59 мА (эффективное значение составляет 41,5 мА) и опережает напряжение по фазе на 90°. Результат соответствует полученным ранее водам. Отметим, что если бы нас интересовала только амплитуда тока, то можно было бы не прибегать к комплексным числам: если А=В/С, то Л=В/С, где А, В, С - амплитуды комплексных чисел. То же самое справедливо и для произведения (см. упражнение 1.17). Для нашего случая

/={ Z=coC{/.

Иногда этот прием очень полезен.

Как ни странно, конденсатор в нашем примере мощность не рассеивает. Его подключение к сети не приводит к увеличению показаний счетчика электроэнергии. Разгадку этой тайны вы узнаете, прочитав следующий раздел. А затем мы продолжим анализ схем, содержащих резисторы и конденсаторы, с помощью обобщенного закона Ома.

Упражнение 1.17. Докажите, что если А=ВС, то А = ВС, где А, В, С - амплитуды комплексных чисел. Подсказка: представьте каждое комплексное число в форме А=Ле<Р.

Мощность в реактивных схемах. Мгновенное значение мощности, потребляемой любым элементом схемы, определяется произведе ниемР=У/. Однако в реактивных схемах, где напряжение U и ток / связаны между собой непростой пропорциональной зависимостью, просто перемножить их нельзя. Дело в том, что могут возникать странные явления, например, знак произведения может изменяться в течение одного периода сигнала переменного тока. Такой пример показан на

рис. 1.46. На интервалах Л и С на конденсатор поступает некоторая мощность (правда, скорость ее изменения переменна), и благодаря этому он заряжается; накапливаемая конденсатором энергия увеличивается (мощность - это скорость изменения энергии). На интервалах В и D потребляемая мощность имеет отрицательный знак - конденсатор

Сииц ,соида

v(i) -(0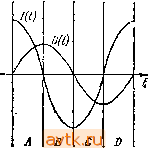

Рис. 1.46.

разряжается. Средняя мощность за период для нашего примера равна нулю; этим свойством обладают все реактивные элементы (индуктивности, конденсаторы и всевозможные их комбинации). Если вы знакомы с интегралами от тригонометрических функций, то следующее упражнение поможет вам доказать это свойство.

Упражнение 1.18. (дополнительное). Докажите, что схема в среднем за полный период не потребляет мощности, если протекающий через нее ток сдвинут по фазе относительно питающего напряжения на 90°,

Как определить среднюю потребляемую мощность для произвольной схемы? В общем случае можно просуммировать произведения UI и разделить сумму на длительность истекшего интервала времени. Иными словами,

т

где Т - полный период времени. Практически так мощность почти никогда не определяют. Нетрудно доказать, что средняя мощность определяется следующим выражением:

P=Re(U4)=Re(lJl*),

где и и I - эффективные комплексные значения напряжения и тока. Рассмотрим пример. Допустим, что в предыдущей схеме конденсатор питается синусоидальным напряжением, эффективное значение которого равно 1 В, Для простоты будем выполнять все преобразования с эффективными значениями. Итак: U=l, I = U/( (oC)=-/соС, Р=

Звездочкой обозначены комплексно-сопряженные величины.- Прим. ред.

i=Re [UI*]=Re(/coC)=0. Мы получили, что средняя мощности, как И утверждалось, равна нулю.

А теперь рассмотрим схему, показанную на рис. 1.47. Выполним ряд преобразований:

Z = ? + (l coC) = /?-(/7й)С), И==и„ I = U/Z = UJ{R - (/VcoC)] l/7a>C)]/[i? + (1/соС^)],

Во второй строке преобразований, при определении тока 1,мы умножили числитель и знаменатель на комплексное число, сопряженное знаменателю, для того чтобы получить в знаменателе действительное число. Полученная величина меньше, чем произведение амплитуд U и Г, ее отношение к этому произведению называют коэффицисп-том мощности: Uocoscolf

\V\\\\ = Ul/[R + {l/(aC)Yf% мощность R

Коэффициент = 1,111,1 =- ., .

мощности [ЛН(1/-с^)]А р„, 47

Коэффициент мощности - это косинус угла, определяющего сдвиг фаз напряжения и тока, он лежит в диапазоне от О (для реактивной схемы) до 1 (для резистивной схемы). Если коэффициент мощности меньше 1, то это значит, что в схеме присутствует реактивный элемент.

Упражнение 1.19. Докажите, что вся средняя мощность предыдущей схемы рассеивается на резисторе. Для того чтобы решить эту задачу, нужно определить величину отношения UVR. Определите, чему будет равна эта мощность в ваттах, если цепь, состоящая из последовательно соединенных конденсаторов емкостью 1 мкФ и резистора сопротивлением 1 кОм, подключена к силовой сети с эффективным напряжением 110 В (частота 60 Гц).

Коэффициент мощности играет немаловажную роль в распределении больших мощностей, так как реактивные токи не передают нагрузке никакой полезной мощности, зато вызывают нагрев в сопротивлениях проводов генераторов и трансформаторов (температура нагрева пропорциональна IR). Бытовые потребители электроэнергии платят только за действительную потребляемую мощность [Re(UI*)l, а промышленные потребители - с учетом коэффициента мощности. Вот почему большие предприятия для погашения влияния индуктивных реактивных сопротивлений производственного оборудования (моторов) сооружают специальные конденсаторные блоки.

Упражнение 1.20. Покажи ге, что пгхледовательное ггодключение конденсатора емкостью С=1 (j)L к последовательной RL-n.enH делает коэффициент мощности этой цепи равным единиие. Затем рассмогрите параллельную цепь и параллельно подключенный ьиидеисатор.

1.19. ЯС-филыры

Благодаря тому что импеданс конденсатора, равный Zc=- соС, зависит от частоты, с помощью конденсаторов и резисторов можно строить частотно-зависимые делители напряжения, которые будут пропускать только сигналы нужной частоты, а все остальные подавлять. В этом разделе вы познакомитесь с примерами простейших RC-фильтров, к которым мы будем неоднократно обращаться в дальнейшем. В гл. 4 и приложении 3 описаны более сложные фильтры.

фильтры высоких частот. На рис. 1.48 показан делитель напряжения, состоящий из конденсатора и резистора.Согласно закону

Ома для комплексных величин,

С

ВЫХ

о

/?-( (оС)

Рис. 1.48.

резисторе R равно

(Окончательный результат получен после умножения числителя и знаменателя на комплексное число, сопряженное знаменателю.) Итак, напряжение на

.= IZn=I/?:

/?2 + (l/u)2C2)

Чаще всего нас интересует не фаза, а амплитуда (/ ых

и.и. = (UsbixULx)= U R/[R -f (l/coC)J v..

Сравните полученный результат с выражением для резистивного делителя:

Us.. = U..RARi + R.).

Векторное представление импеданса RC-mnn (рис. 1.49) показано на рис. 1,50, Итак, если не принимать во внимание сдвиг фаз, а рассмат-

Рис, 1.49.

Рис. 1.50.

[Zno.iiil=V =+(I/(oV); ф=агс18[(-1/(йс)/ ].-

ривать только модули комплексных амплитуд, то отклик схемы будет определяться следующим образом:

f/Bb,x=t/Bx/?/[/?= + (l/ C)]V. =

;=/зх2лда[1-ь(2л/ад/..

График этой зависимости представлен на рис. 1.51. Такой же результат мы бы получили, если бы определили отношение модулей импедан-сов как в упражнении 1.17 и в примере перед этим упражнением; числитель представляет собой модуль импеданса нижнего плеча делителя R, а знаменатель-модуль импеданса последовательного соединения R и С.

Как вы видите, на высоких частотах выходное напряжение приблизительно равно входному: (nl/RC, а на низких

вых/вх С6 дБ/октава)

Рис. 1.51. Частотная характеристика фильтра высоких частот.

частотах выходное напряжение уменьшается до нуля. Мы пришли к важному результату, запомните его. Подобная схема, по понятным причинам, называется фильтром высоких частот. На практике ее используют очень широко. Например, в осциллографе предусмотрена возможность связи по переменному току между исследуемой схемой и входом осциллографа. Эта с^язь обеспечивается с помощью фильтра высоких частот, имеющего перегиб характеристики в области 10 Гц (связь по переменному току используют для того, чтобы рассмотреть небольшой сигнал на фоне большого напряжения постоянного тока).

Обратите внимание, что конденсатор не пропускает ток (/=0). Самый распространенный пример использования конденсатора - это использование его в качестве блокирующего конденсатора постоянного тока. Если возникает необходимость обеспечить связь между усилителями, то почти всегда прибегают к помощи конденсатора. Например, у любого усилителя звуковой частоты высокого класса все входы имеют е.мкостную связь, так как заранее не известно, какой уровень постоянного тока будут иметь входные сигналы. Для обеспечения связи необходимо подобрать R шС таким образом, чтобы все нужные частоты поступали на вход без потерь (без деления на входе).

Часто, например при конструировании фильтров, возникает необходимость определить импеданс конденсатора на некоторой частоте. На рис. 1.52 представлен очень полезный график, охватывающий большой диапазон емкостей и частот для зависимости Z = 1/2л/С

В качестве примера рассмотрим фильтр, показанный на рис. 1.53. Это фильтр высоких частот с точкой перегиба (3 дБ) на частоте 15,9 кГц. Импеданс нагрузки, подключаемой к фильтру, должен быть значительно больше 1 кОм, иначе нагрузка будет искажать выходное напряжение фильтра. Источник сигнала должен обеспечивать возможность подключения нагрузки 1 кОм без значительной аттенюацин (потери амплитуды сигнала), иначе фильтр будет искажать выход источника сигнала.

Фильтры низких частот. Если поменять местами R н С (рис. 1.54), то фильтр будет вести себя противоположным образом в

Глава 1

100 кОм

10к

1кОм

Е 1000м 100м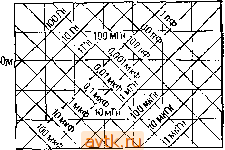

а

ЮГц ЮРГц IkFu, ЮкГц ЮОкГи. ШГи. ЮМЩ ЮОМП Частота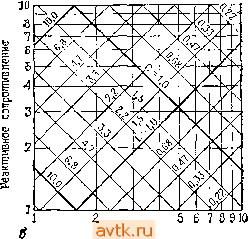

3 4 Частота

- Рис, 1.52. Из.мепение реактивного сопротивления индуктивностей и конденсаторов В зависимости от частоты. Все декады одинаковы и отличаются лишь масштабом (а}, Увеличенное изображение одной декады из графика а; график построен для ставдартных компонентов, имеющих точность 20% (б).

0,01 МкФ

1,0 ком

Рис. 1.53,

Рис. 1,54.

отношении частоты. Можно показать, что ll,,=[\l{\-\-<RCyiAU., График этой зависимости представлен на рис. 1.55. Такой фильтр называют фильтром низких частот. Точка -3 дБ на характеристике фильтра находится на частоте f=l/2nRC. Фильтры низких частот находят j,o очень широкое применение. На- ti

пример, их используют для уст- g ранения влияния близлежащих ir радиостанций на работу усилителей звуковых частот и других =-\/рг чувствительных электронных <здб~7° (поп приборов. масштаб)

Рис. 1.55. Частотная характеристика Упражнение 1.21. Докажите спра- фильтра низких частот, ведливость выражения для выходного напряжения фильтра низких частот.

Выход фильтра низких частот можно рассматривать в качестве самостоятельного источника сигналов. При использовании идеального источника напряжения переменного тока (с нулевым импедансом) фильтр со стороны выхода на низких частотах имеет сопротивление 1 кОм (при расчетах полных сопротивлений идеальный источник сигналов можно заменить коротким замыканием, т. е. его нулевым импедансом для малого сигнала). В выходном импедансе фильтра преобладает емкостная составляющая, и на высоких частотах он становится равным нулю. Для входного сигнала фильтр представляет собой нагрузку, состоящую на низких частотах из сопротивления 1 кОм и сопротивления нагрузки, а на высоких частотах - нагрузку, равную просто сопротивлению 1 кОм.

Частотные характеристика дифференцирующих и й -тегрирующах RC-цепей. Схема дифференцирующей RC-netm, которую мы рассмотрели в разд. 1.14, имеет такой же вид, как и схема фильтра высоких частот. Для того чтобы выходной сигнал был небольшим по сравнению с входным, частота должна быть значительно ниже, чем в точке -3 дБ. В этом легко убедиться. Допустим, что входной сигнал равен и^х=5та)1. Воспользуемся уравнением, которое мы получили ранее для выхода дифференциатора:

тх = sin со/ = (x)RC cos со/.

Отсюда УвыхГ/вх. если сйЯС<1, т. е. RC<\I(u. Если входной сигнал содержит некоторый диапазон частот, то условие должно выполняться для самых высоких частот входного диапазона.

Схема интегрирующей ?С-цепи (разд. 1.15) имеет такой же вид, как и схема фильтра низких частот; аналогично в хорошем интеграторе самые низкие частоты входного сигнала должны сущ,ественно превышать частоту в точке -3 дБ.

конденсатор резистором с таким же, как у конденса- j тора, импедансом (напомним, что ослабление 6 дБ означает уменьшение на-а пряжения вдвое). Дело в

том, что нужно учитывать Рис. 1.56. а ->?С-фильтр в точке 3 дБ; б- пряктиинпрть кпнлрнрятп резистивный делитель: R,R,R{-Q дБ). реактивность конденсато-

1 2 v а / ра, И в этом как раз мо-

жет помочь векторная диаграмма (рис. 1.56). Вдоль осей откладываются действительная (активная или резистивная) и мнимая (реактивная или емкостная) компоненты импеданса. На такой же плоскости можно изображать напряжение (комплексное) в последовательных цепях подобного типа, так как ток в такой цепи во всех точках одинаков. Итак, в нашей схеме (будем рассматривать ее в качестве /?С-делителя напряжения) входное напряжение (приложенное к последовательному соединению резистора R и конденсатора С) пропорционально длине гипотенузы, а выходное напряжение (снимаемое с резистора R) - длине стороны R треуголь-

Индуктивности и конденсаторы. На практике LC-фильтры высоких и низких частот встречаются Kpajine редко, хотя индуктивности в сочетании с резисторами образуют прекрасные схемы фильтров. Это связано с те.м, что индуктивности более громоздки и дороги, а работают хуже, чем конденсаторы (их характеристики более существенно отличаются от идеальных). Если есть возможность выбора, то предпочтение лучше отдать конденсатору. Исключением из этой общей рекомендации являются ферритовые бусины (маленькие тороидальные сердечники) и дроссели в высокочастотных схемах. Несколько бусин нанизывают на провод, благодаря этому соединение, выполненное с помощью провода, становится в некоторой степени индуктивным; импеданс на высоких частотах увеличивается и предотвращает колебания в схеме, при этом, в отличие от /?С-фильтра, активное сопротивление схемы не увеличивается. Радиочастотный дроссель - это катушка, состоящая из нескольких витков провода и ферритового сердечника и используемая с той же целью в радиочастотных схемах.

1.20. Векторные диаграммы

Для анализа реактивных схем очень удобен один графический мо-тод. В качестве примера рассмотрим тот факт, что /?С-фильтр на частоте /= обеспечивает ослабление на 3 дБ. Этот результат мы получили в разд. 1.19. Он справедлив как для фильтров высоких частот, так и для фильтров низких частот. На первый взгляд этот факт может показаться странным, так как на этой частоте реактивное сопротивление конденсатора равно сопротивлению резистора и можно предположить, что ослабление должно составлять 6 дБ. К такому же результату

вы придете, если замените