

 |
 |
|
Разделы
Публикации
Популярные
Новые
|
Главная » Методы подавления шумов, помех электронных систем 1 2 3 4 5 6 7 ... 59 Отсюда следует, что если заряженный конденсатор подключить к резистору, то он будет разряжаться так, как показано на рис. 1.28. Постоянная времена. Произведение RC называют постоянной времени цепи. Если R измерять в омах, а С - в фарадах, то произведение RC будет из.меряться в секундах. Для конденсатора емкостью 1 мкФ, подключенного к резистору сопротивлением I кОм, постоянная времени составляет 1 мс; если конденсатор был предварительно заряжен и напряжение на нем составляет 1 В, то при подключении резистора в цепи появится ток, равный 1 мА. На рис. 1.29 показана несколько иная схема. В момент времени t=0 схема подключается к батарее. Уравнение, описывающее работу такой схемы, выглядит следующим образом: l = C{dUldt) = {U,-U)lR и имеет решение = -Ь Ае- Не пугайтесь, если не поняли, как выполнено математическое преобразование. Важно запомнить полученный результат. В дальнейшем мы будем многократно его использовать, не прибегая к математическим выкладкам. Постоянная величина А определяется из начальных условии (рис. 1.30): t/=0 при /=0, откуда Л=-0, и V =U{\-е- ). и 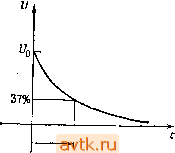 t RC Рис. 1.28. Батарея, напряжение =У^ т -о и о Ркс. 1.29. 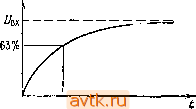 Рис. 1.30. Установление равновесия. При условин tRC напряжение U достигает значения U . (Советуем запомнить хорошее практическое правило, называемое правилом пяти RC. Оно гласит: за время, равное пяти постоянным времени, конденсатор заряжается или разряжается на 99%.) Если затем изменить входное напряжение U (сделать его равным, например, нулю), то напряжение на конденсаторе U будет убывать, стремясь к новому значению по экспоцелдиальному закону g-t/RG Например, если на вход подать прямоугольный сигнал t/x* то сигнал на выходе U будет иметь форму, показанную на рис. 1.31. 
Болез низкая частота Рис. 1.31. Упражнение 1.13. Докажите, что время нарастания сигнала (время, в течение которого сигнал изменяется от 10 до 90% своего максимального значения) составляет 2,2 RC. У вас, наверное, уже возник вопрос: каков закон изменения V {() для произвольного и, {1)? Для того чтобы ответить на него, нужно решить неоднородное дифференциальное уравнение (стандартные г/е-тоды решения таких уравнений здесь не рассматриваются). В результате получим Согласно полученному выражению, /?С-цепь усредняет входное напряжение с коэффициентом пропорциональности e-l, где -т-t. На практике, однако, такой вопрос возникает редко. Чаще всего рассматривают частотные характеристики и определяют, какие изменения претерпевает каждая частотная составляющая входного сигнала. Скоро мы также перейдем к этому немадоважному вопросу. А пока рассмотрим несколько интересных схем, для анализа которых достаточно временных зависимостей. Упрощение с помощью эквивалентного преобразования Тевенина. Можно было бы приступить к анализу более сложных схем, О Рис. 1,32, С -О пользуясь, как и раньше, методом решения дифференциальных уравнений. Однако чаще всего не стоит прибегать к решению дифференциальных уравнений. Большинство схем можно свести к RC-cxeue, показанной на рис, 1.32. Пользуясь эквивалентным преобразованием  КМОП-бцферныв усилители 15 кОм  1±1000пФ А - вход для делителя напряжения, образованного резисторами Ri и Ri, можно определить U (t) для скачка входного напряжения U. Упражнения 1.14. Для схемы, показанной иа рис. 1.32., Ri=R=\0 кОм и С=0,1 мкФ. Определите U(t) и изобразите полученную зависимость в виде графика. Пример: схема задержки. Мы уже упоминали логические уровни - напряжения, определяющие работу цифровых схем. На рис. 1.33 показано, как с помощью конденсаторов можно получить задержанный импульс. В виде треугольников изображены КМОП-буферные усилители. Они дают высокий уровень на выходе для высокого уровня на входе (более половины величины напряжения питания) и наоборот. Первый буферный усилитель воспроизводит входной сигнал и обеспечивает небольшое выходное сопротивление, предотвращая тем самым воздействие на источник сигнала RC-nenv. (вопрос о нагрузке схемы мы рассмотрели в разд. 1.05). Согласно характеристике RC-цепи, выходной сигнал для нее задерживается относительно входного, поэтому выходной буферный усилитель переключается на 10 мкс позже скачка напряжения на входе (напряжение на выходе /?С-цепи достигает 50% своего максимального значения через 0,7 RC). На практике приходится принимать во внимание отклонение входного порога буфера от величины, равной половине напряжения питания, так как это отклонение изменяет задержку и ширину выходного импульса. Иногда подобную схему используют для того, чтобы задержать импульс на время, в течение которого может произойти какое-либо событие. При проектировании схем лучше не прибегать к подобным трюкам, но иногда они бывают полезны. B-RC С - выход- МКО 10 MKG Рис. 1.33. 1.14. Дифференцирующие цепи Рассмотрим схему, изображенную на рис. 1.34, Напряжение на конденсаторе С равно i/-U, поэтому I = Cd{U-U)/dt = U/R. Если резистор и конденсатор выбрать так, чтобы сопротивление R и емкость С были достаточно малыми и выполнялось условие dUldt <UJdt, то C(dUJdt) = U/R или U{t)=-RC[dUit)ldtl Таким образом, мы получили, что выходное напряжение пропорционально скорости изменения входного сигнала. Uit) Рис. 1.34. Рис. 1.,35. Для тога чтобы выполнялось условие dU/dt<dU Jdt, произведение RC должно быть небольшим, но при этом сопротивление R не должно быть слишком малым, чтобы не нагружать вход (при скачке напряжения на входе изменение напряжения на конденсаторе равно нулю и R представляет собой нагрузку со стороны входа схемы). Более точный критерий выбора для R и С мы получим, когда - изучи.м частотные характеристики. Если на - вход схемы подать прямоугольный сигнал, то сигнал на выходе будет иметь вид, представленный на рис. 1.35. Дифференцирующие цепи удобно использовать для выделения переднего и заднего фронтов импульсных сиг-калов, и в цифровых схемах можно иногда встретить цепи, подобные той, которая показана на рнс. 1.36. Дифференцирующая /?С-цепь генериру- к 100 пФ ет импульсы в виде коротких пиков в моменты переключения входного сигнала, а выходной буферный усилитель преобразует эти импульсы в короткие прямоугольные импульсы. В реальных схемах отрицательный пик бывает небольшим благодаря встроенному в буфер вход диоду (речь об этом элементе пойдет в разд. 1.25). К 10 кОи B-RC- IlocnioflHHasr врэме и=1 МКС Паразитная емкостная связь. Иногда схема неожиданно начинает проявлять дифференцирующие свойства, г^тп. причем в ситуациях, где они совершенно нежелательны. При этом можно наблю- Рис. 1.36. дать сигналы, подобные показанным на рис. 1.37. Первый сигнал (а точнее, импульсная помеха) может возникнуть при наличии емкостной связи между рассматриваемой линией и схемой, в которой присутствует прямоугольный сигнал; причиной появления подобной помехи может служить отсутствие оконечного резистора в линии. Если же резистор есть, то еле- дует либо уменьшить сопротивление источника сигналов для линии, либо найти способ ослабления емкостной связи с источником сигналов прямоугольной формы. Сигнал второго типа можно наблюдать в цепи, по которой должен проходить сигнал прямоугольной формы, при наличии дефекта в контакте с этой цепью, например в щупе осциллографа. Небольшая емкость, возникающая при плохом контакте, и входное сопротивление осциллографа об- -- разуют дифференцирующую цепь. Если вы р^. j 37 обнаружили, что ваша схема что-то дифференцирует, то сказанное может помочь вам найти причину неисправности и устранить ее. 1.15. Интегрирующие цепи Рассмотрим схему, изображенную на рис. 1.38. Напряжение на исторе R равно и^-и, следовательно, I=C{dU/dt)=(U-U)/R. 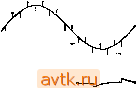 резисторе R равн R Рис. 1.38. Если обеспечить выполнение условия -о и<и^ за счет большого значения произ-rj ведения RC, то получим c{dUldt)wUJR или и {1.) = -щ.11 (т) dx + константа. Мы получили, что схема интегрирует входной сигнал по времени! Рассмотрим, каким образом эта схема обеспечивает аппроксимацию интегрирования в случае входного сигнала прямоугольной формы: и (О представляет собой знакомый нам уже график экспоненциальной зависимости, определяющей заряд конденсатора (рис. 1.39). Первый участок экспоненты (интеграл от почти постоянной велнчи-1гы) - прямая с постоянным углом наклона; при увеличении постоянной времени RC используется все меньший начальный участок экспоненты, тем самым обеспечивается лучшая аппроксимация идеального пилообразного сигнала. Отметим, что условие U<U равносильно тому, что ток пропорционален
и Ошибка , 10% при Линейная зависимость напряжению (7в^. Если бы в качестве Рис. 1.39. входного сигнала выступал ток /(/), а не напряжение, то мы получили бы идеальный интегратор. Источником тока может служить резистор с большим сопротивлением и с большим падением напряжения на кем, и на практике часто пользуются этим приближением. В дальнейшем, когда мы познакомим вас с операционными усилителями и обратной связью, вы узнаете, как построить интегратор, не прибегая к условию U <Uj,. Такой интегратор работает в широком диапазоне частот и напряжений с пренебрежимо малой ошибкой. Интегрирующие цепи находят широкое применение в аналоговой технике. Их используют в управляющих системах, схемах с обратной связью, при аналого-цифровом преобразовании и генерации колебаний. Генераторы пилообразного сигнала. Теперь вы без труда разберетесь в том, как работает генератор пилообразного сигнала. Эта схема хорошо зарекомендовала себя и нашла очень широкое применение: ее используют во время-задающих схемах, в генераторах синусоидальных и других типов колебаний, в схемах развертки осциллографов, в аналого-цифровых преобразователях. Она показана на рис. 1.40. -О Ыулц, и О Рис. 1.40,  Рис. 1.41. Из уравнения для тока, протекающего через конденсатор, I=C(dU/dt) получим и{t)= (I/C)t. Выходной сигнал изображен на рис. 1.41. Линейное нарастание сигнала прекращается тогда, когда иссякает напряжение источника тока, т. е. достигается его предельное значение. Кривая для простой /?С-цепи с резистором, подключенным к источнику напряжения, ведет себя аналогично случаю достижения предела источником тока. На рис. 1.41 эта вторая кривая показана для случая, когда R выбрано так, чтобы ток при нулевом выходном напряжении был равен току источника тока; при этом вторая кривая стремится к тому же пределу, что и ломаная. (В реальных источниках тока выходное напряжение ограничено напряжением используемых в них источников питания, так что такое поведение вполне правдоподобно.) В следующей главе, посвященной транзисторам, мы построим простые схемы ИСТ0Ч1ШК0В тока, а в главах, где рассматриваются операционные усилители и полевые транзисторы,- их усовершенствованные типы. Бот как много интересных вопросов ожидает нас впереди. Упражнение t.!5. Ток 1 мА заряжает конденсатор емкрстыо 1 мкФ. Через какое время напряжение достигнет 10 В? ИНДУКТИВНОСТИ и ТРАНСФОРМАТОРЫ 1.16. Индуктивности Если вы поняли, что такое конденсатор, то вы поймете и что такое индуктивность (рис. 1.42). Сравним индуктивность и конденсатор меж;у собой; в индуктивности скорость изменения тока зависит от приложенного напряжения, а в конденсаторе скорость изменения на- ~VV-V> Рис. 1.42. пряжения зависит от протекающего тока. Уравнение индуктивностг. имеет следующий вид: U=L{dI/dt), где L - индуктивность в генри (или мГн, мкГн и т. д.). Напряжение, приложенное к индуктивности, вызывает нарастание протекающего через нее тока, причем изменение тока происходит по линейному закону (если пропустить ток через конденсатор, то это приведет к нарастанию напряжения ня нем, причем изменение напряжения будет происходить по линейному закону); напряжение величиной 1 В, приложенное к индуктивностг I Гн, приводит к нарастанию тока через индуктивность со скоростью 1 А в 1с. Условно индуктивность изображают в виде нескольких витков провода - такую конструкцию имеет простейшая индуктивность. Другие, более совершенные конструкции включают сердечник, на который наматывается провод. Материалом для сердечника чаще всего служит железо (пластинки, прокатанные из сплавов железа или изготовленные методами порошковой металлургии) или феррит, представляющий собой хрупкий непроводящий магнитный материал черного цвета. Сердечник позволяет увеличить индуктивность катушки за счет магнитных свойств материала сердечника. Сердечник может быть изготовлен в виде бруска, тора или может иметь какую-нибудь более причудливую форму, например горшка (описать его словами не так-то просто: представьте себе форму для выпечки пончиков, которая разнимается пополам). Индуктивности находят наибольшее применение в радиочастотных схемах, где они используются в качестве радиочастотных дросселей, и в резонансных схемах. Пара связанных индуктивностей образует такой интересный элемент, как трансформатор. О нем мы поговорим в следующем разделе. По сути дела индуктивность - это противоположность конденсатора. Последующие разделы этой главы, в которых вводится такое важное понятие, как полное сопротивление, или импеданс, покажут вам, в чем эта противоположность проявляется. 1.17. Трансформаторы Г Трансформатор - это устройство, состоящее из двух связанных катушек индуктивности (называемых первичной н вторичной обмотками). Напряжение, сни.маемое со вторичной обмотки, иное по сравнению с напряжением переменного тока, поданным на первичную обмотку, причем коэффициент изменения (трансформации) пропорционален otj ношению числа витков обмоток трансформатора. Ток во вторичной обмотке соответственно также отличается от тока в первичной. На рис. 1.43 показано условное обозначение трансформатора с пластинчатым сердечником (трансформаторы такого тппа используются для преобразования напряжения переменного тока с частотой 50 или 60 Гц). Трансформатор обладает весьма высоким коэффициентом полезного действия (мощность на его Рис. 1.43. выходе почти равна мощности на входе); в связи с этим повышающий трансформатор обеспечивает рост напряжения при уменьшении тока. Немного забегая вперед, отметим, что трансформатор с отношением числа витков обмоток равным п изменяет полное сопротивление в раз. Если вторичная обмотка не нагружена, то в первичной протекает очень небольшой ток. В эл§ктронных приборах трансформаторы выполняют две важные функции; во-первых, они преобразуют напряжение переменного тока сети к нужному, обычно более низкому значению, которое можно использовать в схеме, и, во-вторых, они изолируют электронную схему от непосредственного контакта с силовой сетью, так как обмотки трансформатора электрически изолированы одна от другой. Выпускаемые промышленностью силовые трансформаторы (предназначенные для работы с напряжением силовых сетей, равным ПО, 127 или 220 В) обеспечивают разнообразные значения вторичных напряжений и токов: диапазон напряжений включает значения от 1 В до нескольких тысяч вольт, диапазон тока - от нескольких миллиампер до сотен ампер. Трансформаторы, используемые обычно в электронных приборах, обеспечивают диапазон вторичного напряжения от 10 до 50 В, диапазон тока - от 0,1 до 5 А. Промышленность выпускает также трансформаторы, предназначенные для работы в диапазоне звуковых частот и радиочастот. В диапазоне радиочастот, для узких диапазонов частот, иногда используют резонансные трансформаторы. Интерес представляют трансформаторы для линий передач, о которых мы немного поговорим в гл. 13, в разд. 13.10. Для сердечников высокочастотных трансфоматоров используют специальные^материалы или прибегают к специальным конструкциям для того, чтобы уменьшить потери энергии в сердечнике; что же касается сердечников низкочастотных (т. е. силовых) трансформаторов, то их делают тяжелыми и крупногабаритными. Трансформаторы для высоких и низких частот, вообще говоря, не взаимозаменяемы. ПОЛНОЕ И РЕАКТИВНОЕ СОПРОТИВЛЕНИЕ Замечание: этот раздел содержит много математических выкладок; при желании их можно пропустить, но ни в коем случае не упускайте из внимания результаты. Схемы с конденсаторами и индуктивностями сложнее, чем рассмотренные ранее резистивные схемы,- их работа зависит от частоты входного сигнала; как мы уже убедились, они искажают такие входные сигналы, как, например, прямоугольные колебания. Тем не менее, оказывается, можно обобщить закон Ома, заменив понятие сопротивление понятием полное сопротивление , или импеданс , тогда он будет справедлив для любой схемы, в состав которой входят линейные пассивные элементы (резисторы, конденсаторы, индуктивности). Итак, понятия импеданс и реактивное сопротивление делают закон Ома справедливым для схем, содержащих конденсаторы и индуктивности. Уточним терминологию. Импеданс - это обобщенное или полное сопротивление; индуктивности и конденсаторы обладают реактивным сопротивлением (можно сказать, что они реагируют на воздействие); резисторы обладают сопротивлением (по аналогии они оказывают сопротивление воздействию). Иными словами, импеданс = сопротивление + реактивное сопротивление (более подробно поговорим об этом позже). Однако можно встретить, например, такое выражение: импеданс конденсатора па данной частоте составляет... Дело в том, что в импеданс входит реактивное сопротивление, и поэтому не обязательно говорить реактивное сопротивление конденсатора , можно сказать и импеданс конденсатора . На самом деле слово импеданс часто употребляют и тогда, когда известно, что речь идет о сопротивлении; например, говорят импеданс источника пли выходной импеданс , имея в виду эквивалентное сопротивление некоторого источника. То же самое относится и к входному импедансу . В дальнейшем речь пойдет о схемах, для питания которых используется синусоидальный сигнал с определенной частотой. Анализ схем, работающих с сигналами другой фор.мы, требует большей тщательности и предполагает использование уже известных нам методов (например, метода дифференциальных уравнений или метода преобразования Фурье, при котором сигнал представляют в виде ряда синусоид). На практике эти методы редко используются. 1.18. Частотный анализ реактивных схем Для начала рассмотрим конденсатор, на который подается синусоидальное напряжение источни.ка питания (рис. 1.44). Ток в схеме определяется следующим образом: I{t)=C{dU/dt)=Ci>>UoCOS at. Из этого уравнения следует, что ток имеет амплитуду / и опережает входное напряжение по фазе на 90°. Если не принимать во внимание со- отношение фаз, то /=:{;/(1/(оС). Uq sin ul Рис. 1.44. 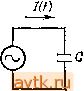 (Напомним, что (о = 2я/.) Конденсатор ведет себя как резистор, сопротивление которого зависит от частоты и определяется выражением R = 1/соС, и, кроме того, ток, протекающий через конденсатор, сдвинут по фазе на 90° относительно напряжения (рис. 1.45). Например, через конденсатор емкостью 1 мкФ, подключенный к силовой сети с напряжением 110 В (эффективное значение) и частотой 60 Гц, будет протекать ток, эффективная амплитуда которого определяется следующим образом: / = 110/[1/(2я-60 X X 10-)1 = 41,5 мА (эффективное значение). Замечание: сейчас нам необходимо воспользоваться комплексными переменными; при желании вы можете пропустить математические выкладки, приводимые в последующих разделах, и принять на веру полученные результаты (они выделены в тексте). Не думайте, что подробные алгебраические преобразования, приводимые в этих разделах, необходимы для понимания всего остального материала книги. Это не так - глубокое знание математики похвально, но совсем не обязательно. Следующий раздел, пожалуй, наиболее труден для тех, у кого нет достаточной математической подготовки. Но пусть вас это не огорчает. Определение напряжения и тока с помощью комплексных чисел. Только что вы убедились в том, что в цепи переменного тока, работающей с синусоидальным сигналом некоторой частоты, возможен сдвиг по фазе между напряжением и током. Тем не менее если схема содержит только линейные элементы (резисторы, конденсаторы индуктивности), то амплитуда токов на всех участках схемы про порциональна амплитуде питающего напряжения. В связи с этим можно попытаться найти некоторые общие выражения тока, напря жения и сопротивления и обобщить тем самым закон Ома. Оче видно, что для того, чтобы определить ток в какой-либо точке схемы недостаточно задать одно значение - дело в том, что ток характе ризуется как амплитудой, так и сдвигом фазы. Конечно, можно определять амплитуды ифазовыесдвигинапряже НИИ и токов явно, например U(t) =23,7 sin (377г'--0,38), но оказывает ся, что проще это делать с помощью комплексных чисел. Вместо того чтобы тратить время и силы на сложение и вычитание синусоидальных функций, можно легко и просто складывать и вычитать комплексные 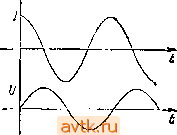 Рис. 1.45. 1 2 3 4 5 6 7 ... 59 |
||||||||||||||||||
|
© 2004-2025 AVTK.RU. Поддержка сайта: +7 495 7950139 в тональном режиме 271761
Копирование материалов разрешено при условии активной ссылки. |