Основы электроники 81

больше, чем сигнал У. Во многих случаях именно так и производят сравнение. Но очень часто подобные отношения достигают миллионов, и тогда удобнее пользоваться логарифмической зависимостью и измерять отношение в децибелах (децибел составляет одну десятую часть бела, но единицей бел никогда не пользуются). По определению отношение двух сигналов, выраженное в децибелах, это

дБ=20 \g{AJA),

где Ai и Ai- амплитуды двух сигналов. Например, если один сигнал имеет амплитуду вдвое большую, чем другой, то отношение первого сигнала ко второму составляет +6 дБ, так как Ig 2=0,3010. Если один сигнал в 10 раз больше другого, то отношение первого ко второму составляет +20 дБ, а если один сигнал в 10 раз меньше другого, то -20 дБ. Отношение мощностей двух сигналов определяется так;

дБ=10 1е(Р./Л),

где Pi и Pi- мощности двух сигналов. Если оба сигнала имеют одну и ту же форму, то есть представлены синусоидами, то оба способа определения отношения сигналов (через амплитуду и мощность) дают одинаковый результат. Для сравнения сигналов разной формы, например синусоидального и шумового, следует использовать мощность (или эффективные значения).

Хотя децибел служит для определения отношения двух сигналов, иногда эту единицу используют для измерения абсолютного, а не относительного значения амплитуды. Дело в том, что можно взять некоторую эталонную амплитуду и определять любую другую амплитуду в децибелах по отношению к эталонной. Известно несколько стандартных значений амплитуды, используемых для такого сравнения (эти значения не указываются, но подразумеваются); приведем некоторые из них: а) дБВ - эффективное значение 1 В; б) дБВт - напряжение, соответствующее мощности 1 мВт на нагрузке 600 Ом (эффективное значение около 0,78 В); в) дБп - небольшой шумовой сигнал, генерируемый резистором при комнатной тетлпературе (об этом более подробно пойдет речь в разд. 7.10). Помимо перечисленных существуют эталонные сигналы для измерений в других областях. Например, в акустике уровень звукового давления О дБ соответствует сигналу, среднее квадратурное давление которого составляет 0,0002 мкбар (1 бар равен 10 дин на квадратный сантиметр или приблизительно 1 атмосфере); в связи уровни определяются в дБС (относительный шум в полосе частот с весовой функцией С). Обращаем ваше внимание на эталонную амплитуду О дБ: пользуясь этим значением, не забывайте его оговорить, например амплитуда 27 дБ относительно эффективного значения 1 В , или в сокращенной форме 27 дБ относительно 1 В^фф , или пользуйтесь условным обозначением дБ В.

Упражнение 1.11. Отношение двух сигналов составляет: а) 3 дБ, б) 6 дБ, в) 10 дБ, г) 20 дБ, Для каждого случая определите отношение напряжений и мощностей сигналов.

Г лапа f

1.09. .Другие типы сигналов

Линейно-меняющийся сигнал. Линейно-меняющийся сигнал (показан на рис. 1.15) - это напряжение, возрастающее (или убывающее) с постоянной скоростью. Напряжение, конечно, не может расти.

Рис. 1.15.

Рис. 1.16.

бесконечно. Поэтому обычно такое напряжение имеет вил, показанный на графике рис. 1.16,-напряжение нарастает до конечного значения, или на графике рис. 1.17- пилообразное напрялсение.

Рис. 1.17,

Рис. 1.13.

Треугольный сигнал. Треугольный сигнал приходится ближайшим родственником линейно-меняющемуся сигналу; отличие состоит в том, что график треугольного сигнала является симметричным (рис. I.I8).

Сигналы шум0в^\ Сигналы, о которых пойдет речь, очень часто смешивают с шумами, имея в виду только тепловые случайные шумы. Шумовые напряжения характеризуются частотным спектром (произведение мощности на частоту в герцах) и распределением амплитуд. Одним из наиболее распространенных типов шумовых сигналов является бешй шум с гауссовым распределением в ограниченном спектре частот. Для такого сигнала произведение мощности на частоту в герцах сохраняется постоянным в некотором диапазоне частот, а вариации а.мплитуды для большого числа измерений мгновенного значения описываются законом распределения Гаусса. Шулювой сигнал такого типа генерирует резистор (шум Джонсона), и он создает неприятности при всевозможных измерениях, в которых требуется высокая чувствительность. На экране осциллографа мы видим шумовой сигнал таким,

Имеются в виду случайные Сигналы,- Прим, ред.

JOK он показан на рис. 1.19. Более подробно шумовые сигналы и способы борьбы с шумовыми помехами будут рассмотрены в гл. 7. В разд. 9.35 рассматриваются вопросы генерации шумовых сигналов.

Рис. 1.19.

Прямоугольные сигналы. График изменения прямоугольного сигнала во времени показан на рис. 1.20. Как и синусоидальный, прямоугольный сигнал характеризуется амплитудой и частотой. Если на вход линейной схемы подать прямоугольный сигнал, то сигнал на выходе вряд ли будет иметь прямоугольную форму. Для прямоугольного

100% 90%

If f

Рис. 1.20.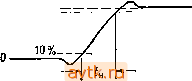

Рис. 1.21.

сигнала эффективное значение равно просто амплитуде. Форма реалыю-го прямоугольного сигнала отличается от идеального прямоугольника; обычно в электронной схеме время нарастания сигнала t составляет от нескольких наносекунд до нескольких микросекунд. На рис. 1.21 показано, как обычно выглядит скачок прямоугольного сигнала. Время нарастания определяется как время, в течение которого сигнал нарастает от 10 до 90% своей максимальной амплитуды.

Импульсы. Иипулъсы-это сигналы, показанные на рис. 1.22. Они характеризуются амплитудой и длительностью импульса. Если

Рис. 1.22.

генерировать периодическую последовательность импульсов, то можно говорить о частоте, или скорости повторения, импульса и о рабочем цикле , равном отношению длительности импульса к периоду повторения (рабочий цикл лежит в пределах от О до 100%) Импульсы мо-

1> в отечественмой литературе величину, обратную этому параметру, называют скважностью,- Прим, перев,

Глава 1

гут иметь положительную или отрицательную полярность (пьедестал), кроме того, они могут быть нарастающими или спадающими. Например, второй импульс, показанный на рис. 1.22, является убывающим импульсом положительной полярности (или спадающим импульсом с положительным пьедесталом).

Сигналив виде скачков и яюков. Сигналы в виде скачков и пиков упоминаются часто, но широкого применения не находят. К иХ

Пик

Рис. 1.23.

помощи прибегают для описания работы схем. Если попытаться их нарисовать, то они будут выглядеть так, как показано на рис. 1.23. Скачок представляет собой часть прямоугольного сигнала, а пик - это два скачка, следующие с очень коротким интервалом.

ЛОГИЧЕСКИЕ УРОВНИ

На рис. 1.24 показаны диапазоны напряжения, соответствующие двум логическим уровням (высокому и низкому) для трех наиболее распространенных сел1ейств цифровых элементов. Для каяюго семейства определены допустимые значения как выходного, так и входного напряжений, соответствующие двум уровням - высокому н низкому,

Низкий Высокий

Нровень уровень

ТТЛ

0 1 2 3 4 5

зле 10ООО i j L iA JL i

кмогт

о 1

кмол Ti I J

8 10 J2

Plic, 1.24.

Выделенные области над горизонтальной осью показывают установленные диапазоны, в пределах которых должен находиться каждый из логических уровней выходного напряжения. Стрелками указаны значения напряжений (дая высокого и низкого уровней), ставшие типовыми на практике. Заштрихованные области под горизонтальной осью показывают установленные диапазоны, в пределах которых должны находиться логические уровни входного напряжения. Отдельными стрелками указаны типовые значения порогового напряжения, представляющего собой границу между высоким низким логическим уровнями. Во всех случаях высокий логический уровень более положителен, чем низкий.

Несколько слов следует сказать о том, какой смысл имеют минимальные, типовые и максимальные значения, указываемые в спецификациях на электронные приборы. Вообще говоря, фирма-изготовитель гарантирует, что значения параметров элементов

будут лежать в диапазоне между максимальным и минимальным значениями, причем для большинства элементов они будут близки к типовым. Типовые значения - это те значения, которые используются при проектировании схем; однако проектировать схемы нужно так, чтобы они правильно работали во всем диапазоне изменения параметров - от минимального до максимального значения (экстремальные значения, получающиеся при производстве схем). В частности, хорошая схема сохраняет работоспособность и при наихудшем сочетании минимальных и максимальных значений параметров элементов. Про такую схему говорят, что она спроектирована с учетом работы в жестких условиях, Диапазон изменения параметров следует учитывать для всякой схемы, собираемой из неотобранных компонентов,

1.10. Логические уровни

Импульсы и прямоугольные сигналы широко используются в цифровой электронике. В цифровой схеме состояние любой точки в любой момент времени определяют заранее известные уровни напряжения. Эти уровни называют просто высокий и низкий . Они соответствуют значениям ложь (0) и истина (1) булевой алгебры логики, которая имеет дело с переменными, принимающими эти значения.

В цифровой электронике точные значения напряжений не играют роли. Задача состоит в том, чтобы различать только уровни напряжения. В связи с этим для каждого семейства цифровых логических элементов определены допустимые значения высокого и низкого уровня напряжения. На рис. 1.24 указаны значения логических уровней для трех широко распространенных семейств цифровых элементов (КМОП-элементы работают при напряжениях от +3 до +18 В; на рисунке указаны два типовых значения, которыми пользуются на практике),

1.11. Источники сигналов

Нередко источник сигнала входит как неотъемлемая часть в саму схему. Но для испытательного режима работы очень удобен отдельный независимый источник сигнала. В качестве такого источника могут выступать три типа приборов: генераторы (синусоидальных) сигналов, генераторы импульсов и генераторы функций (сигналов специальной формы).

Генераторы (синусоидальных) сигналов. Генераторами сигналов называют генераторы синусоидальных колебаний, которые обычно обеспечивают широкий диапазон частот (как правило, от 50 кГц до 50 МГц) и приспособлены для тонкой регулировки амплитуды (для этой цели используется схема резистивного делителя, называемого аттенюатором). В некоторых генераторах предусмотрена возможность модуляции выходного сигнала (см. гл. 13). Одной из разновидностей генератора сигнала является свип-генератор (генератор качающейся частоты) - он может периодически производить развертку выходной частоты в некотором диапазоне частот. Это качество прибора очень полезно при испытаниях схем, свойства которых определенным обра- сом зависят от частоты (например, резо11ансные схемы или фильтры) 2*

в наши дни эти и многие другие приборы выпускаются в исполнении, позволяющем задавать (программировать) частоту, амплитуду и другие параметры с помощью вычислительной машины или другого цифрового устройства.

Еще одной разновидностью генераторов сигналов является снн-тезатор частот - устройство, которое позволяет производить точную установку частоты генерируемых синусоидальных колебаний. Частота задается цифровым способом, часто с точностью до восьми знаков после запятой или более, и синтезируется с помощью точного эталона кварцевого генератора цифровыми методами, о которых речь пойдет позже (в разд. 9.28-9.33). Если перед вами когда-нибудь будет стоять задача получения сигнала с абсолютно достоверным, точным значением частоты, то без синтезатора ее не решить.

Генераторы импульсов. Генераторы импульсов всего лишь формируют импульсы, но как совершенно они выполняют свою задачу! В них предусмотрена возможность регулировки ширины (длительности) импульса, частоты повторения, амплитуды, времени нарастания и других параметров. Кроме того, многие генераторы позволяют генерировать пары импульсов с заданными интервалами и частотой повторения и даже кодовые последовательности импульсов. В большинстве современных генераторов импульсов предусмотрены логические выходы, обеспечивающие легкое сопряжение с цифровыдн! схемами. Как и в генераторах синусоидальных сигналов, в генераторах импульсов часто предусмотрено внешнее программирование.

Генераторы функций (специальных сигналов). Во многих отношениях генераторы функций являются наиболее гибкими из всех источников сигналов. Они позволяют формировать синусоидальные, треугольные, прямоугольные сигналы в очень широком диапазоне частот (от 0,01 Гц до 10 МГц), при этом предусмотрена возможность регулировки амплитуды и смещения по постоянному току (постоянное напряжение, добавляемое к сигналу). Многие генераторы функций могут производить развертку частоты, причем в нескольких режимах (линейное или логариф.мическое изменение частоты во времени). Промышленность выпускает генераторы функций с импульсным выходом (правда, они не обладают гибкостью генераторов импульсов) и возможностью модуляции выходного сигнала.

Промышленность выпускает также программируемые и цифровые генераторы функций. В цифровых генераторах значение частоты (а иногда и амплитуды) считывается в цифровом виде. В последние годы семейство генераторов функций пополнилось синтезирующим гене-раторо.м функций (генератором - синтезатором функций) - устройством, которое сочетает в себе гибкость генератора функций со стабильностью и точностью синтезатора частот. И последнее: если вам хотелось бы иметь один источник сигналов на все случаи жизни, то для этой цели лучше других подойдет генератор функций.

КОНДЕНСАТОРЫ И ЦЕПИ ПЕРЕМЕННОГО ТОКА

Коль скоро мы начинаем рассматривать изменяющиеся сигналы напряжения и тока, нам необходимо познакомиться с двумя очень занятными элементами, которые не находят применения в цепях постоянного тока,- речь идет о конденсаторах и индуктивностях. Скоро вы убедитесь, что эти компоненты вместе с резисторами являются основными элементами пассивных линейных цепей, составляющих основу почти всей схемотехники. Особенно следует подчеркнуть роль конденсаторов - без них не обходится почти ни одна схема. Они используются при генерации колебаний, в схемах фильтров, для блокировки и шунтирования сигналов. Их используют в интегрирующих и дифференцирующих схемах. На основе конденсаторов и индуктивностей строят схемы формирующих фильтров для выделения нужных сигналов из фона. Некоторые примеры подобных схем вы найдете в этой главе, а еще большее число интересных примеров использования конденсаторов и индуктивностей встретится вам в последующих главах.

Приступим к более детальному изучению конденсаторов. Явления, протекающие в конденсаторе, описываются математическими зави-симостя.ми, поэтому читателям, которые имеют недостаточную подготовку в области математики,полезно прочитать приложение Б. Не огорчайтесь, если некоторые детали не будут сразу вполне понятны, главное - это общее понимание вопроса.

1.12. Конденсаторы

В первом приближении конденсаторы (рис. 1.25) - это частот1Ю-зависимые резисторы. Они позволяют создавать, например, частотно-зависимые делители напряжения. Для решения некоторых задач

-j 1- Рис. 1.25.

(шунтирование, связывание контуров) больших знаний о конденсаторе н не требуется, другие задачи (построение фильтров, резонансных схем, накопление энергии) требуют более глубоких знаний. Например, конденсаторы не рассеивают энергию, хотя через них и протекает ток,- дело в том, что ток и напряжение на конденсаторе смещены друг относительно друга по фазе на 90°.

Конденсатор - это устройство, имеющее два вывода и обладающее следующим свойством:

Конденсатор, имеющий емкость С фарад, к которому приложено напряжение и вольт, накапливает заряд Q кулон.

Продифференцировав выражение для Q (см. приложение Б), полу ,чим

Итак, конденсатор - это более сложный элемент, чем резистор; ток пропорционален не просто напряжению, а скорости изменения напряжения. Если напряжение на конденсаторе, имеющем емкость I Ф, изменится на 1 В за 1 с, то получим ток 1 А. И наоборот, протекание тока 1 А через конденсатор емкостью 1 Ф вызывает изменение напряжения на I В за 1 с. Емкость, равная одной фараде, очень велика, и поэтому чаще имеют дело с микрофарадами (мкФ) или пикофарадами

Рис. 1.26.

(пФ). (Для того чтобы сбить с толку непосвященных, на принципиальных схемах иногда опускают обозначения единиц измерения. Их приходится угадывать из контекста.) Например, если подать ток 1 мА на конденсатор емкостью 1 мкФ, то напряжение за 1 с возрастет на 1000 В. Импульс тока продолжительностью 10 мс вызовет увеличение напряжения на конденсаторе на 10 В (рис. 1.26).

Промьшленность выпускает конденсаторы разнообразных форм и размеров; через некоторое время вы познакомитесь с наиболее распространенными представителями этого обширного семейства. Простейший конденсатор состоит из двух проводников, расположенных на небольшом расстоянии друг от друга (но не соприкасающихся между собой); настоящие простейшие конденсаторы имеют именно такую конструкцию. Чтобы получить большую емкость, нужны большая площадь и меньший зазор между проводниками; обычно для этого один из проводников покрывают тонким слоем изолирующего материала (называемого диэлектриком), для таких конденсаторов используют, например, алитированную (покрытую алюминием) майларовую пленку. Широкое распространение получили следующие типы конденсаторов: керамические, электролитические (изготовленные из металлической фольги с оксидной пленкой в качестве изолятора), слюдяные (изготовленные из металлизированной слюды). Каждому типу конденсаторов присущи свои качества; краткий перечень отличительных особенностей каждого типа конденсаторов приведен мелким шрифтом в разделе Конденсаторы . В общем, можно сказать, что для некритичных схем подходят керамические и майларовые конденсаторы; в схемах, где требуется большая емкость, применяются танталовые конденсаторы, а для фильтрации в источниках питания используют электролитические конденсаторы.

Параллельное и последовательное соединение конденсат торос. Емкость несколькнх-пэраллельно соединенных конденсаторов

равна сумме их емкостей. Нетрудно в этом убедиться; приложим напряжение к параллельному соединению, тогда

си Q= Qi+Q2+ Qz+ . =с,и+с^и+с,и + ... {С,+С, + С,+ ...)и

или

С = С, + С,+С,+ ... .

Для последовательного соединения конденсаторов имеем такое же выражение, как для параллельного соединения резисторов:

l/Ci+I/Ca+l/Ca*

В частном случае для двух конденсаторов

C=CiCJ{C+C,).

КОНДЕНСАТОРЫ

Промышленностью выпускается много типов конденсаторов. Здесь перечислены основные преимущества и недостатки различных типов. Очевидно, что данная оценка имеет несколько субъективный характер (см, таблицу на стр. 40).

Упражнение 1.12. Получите выражение для емкости двух последовательно соединенных конденсаторов. Подсказка: так как точка соединения конденсаторов не имеет внешних подключений, то заряд, накопленный двумя конденсаторами, должен быть одинаков,

1.13. 7?С-цепи: изменения во времени напряжения и тока

Для анализа цепей переменного тока (или в общем случае схем, работающих с изменяющимися напряжениями и токами) можно использовать характеристики двух типов. Во-первых, можно рассматривать изменения напряжения U и тока / во времени, а во-вторых,- изменение амплитуды при изменении частоты сигнала. И те и другие характеристики имеют свои преимущества, и в каждом практическом

случае приходится выбирать наиболее подходящие. Мы j-.

начнем изучение цепей переменного тока с временных А ! зависимостей, а в разд. 1.18 перейдем к частотным ха- R рактеристикам.

Каковы же свойства схем, в состав которых входят pj,g 1 27. конденсаторы? Для того чтобы ответить на этот вопрос, рассмотрим простейшую iC-цепь (рис. 1.27). Воспользуемся полученным ранее выражением для емкости:

C{dU/dt) = I=-U/R.

Это выражение представляет собой дифференциальное уравнение, решение которого имеет вид

Тип

Примечания

Слюдяной

Цилиндрический керамический

Керамический

Майларовые

Полистироловые

Поликарбонат-

иые Стеклянные

Фарфоровые

Танталовые

Электролитические

Масляные

Очень хорошие; рекомендуются для радиочастот

Очень малая емкость; несколько значений температурного коэффициента, включая О

Малые габариты, недороги, широко используются, возможен собственный резонанс ~100 кГц

Хорошие, недорогие, широко используются

Высококачественные, крупногабаритные, рекомендуются для фильтров

Высококачественные, рекомендуются для интегрирующих схем

Стабильны при длительной эксплуатации

Хорошие, недорогие, стабильные при длительной эксплуатации

Большая емкость с приемлемой утечкой, малогабаритные, поляризованные, небольшая индуктивность, широко используются

Рекомендуется использовать только в составе фильтров источников питания (в остальных случаях заменять танталовыми)-, поляризованные, короткий срок службы

Высоковольтные фильтры; крупногабаритные, длительный срок службы

) Хотя параметры, по выражению авторов, ужасны , ио ие надо забывать, что у электролитических конденсаторов самая большая удельная и абсолютная емкость, пока недостижимая в других типах. - Прим. р^д