фактом (имеется в виду теорема об эквивалентном преобразовании схем). А сейчас немного отвлечемся от нашей темы и поговорим об источниках тока и напряжения.

1.04. Источники тока и напряжения

Идеальный источник напряжения - это черный ящик , имеющий два вывода, между которыми он поддерживает постоянное падение напряжения независимо от величины сопротивления нагрузки. (Это означает, например, что он должен порождать ток, равный I=UIR, если к выводам подключить резистор с сопротивлением R.) Реальный источник напряжения не может дать ток, больший некоторого предельного максимального значения, и в общем случае ои ведет себя как идеальный источник напряжения, к которому последовательно подключен резистор с небольшим сопротивлением. Очевидно, чем

ЛЛ ЛА

+5 В

+15 В

Батарея -

Pl!C. 1.6.

Источник питания

меньше сопротивление этого последовательно подключенного резистора, тем лучше. По понятным причинам источник напряжения предпочитает нагрузку в виде разомкнутой цепи, а нагрузку в виде замкнутой цепи недолюбливает . Условные обозначения источников напряжения приведены на рис. 1.6.

Идеальный источник тока - это черный ящик , имеющий два вывода и поддерживающий постоянный ток во внешней цепи независимо от величины сопротивления нагрузки и приложенного напряжения. Для того чтобы выполнять свои функции, он должен уметь поддерживать любое нужное напряжение между своими выводами. Реальные источники тока (самая нелюбимая тема для большинства учебников) имеют ограниченный диапазон, в котором может изменяться создаваемое ими напряжение (он называется рабочим диапазоном выходного напряжения или просто диапазоном), и, кроме того, выходной ток источника нельзя считать абсолютно постоянным. Источник тока предпочитает нагрузку в виде замкнутой цепи, а нагрузку в виде разомкнутой цепи недолюбливает . Условные обозначения источника тока приведены на рис. 1.7.

© ф

I 1мА

\ 1мА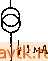

Рис. 1.7.

Хорошим примером источника напряжения может служить батарея (для источника тока подобной аналогии найти нельзя). Например, стандартная батарейка от карманного фонаря обеспечивает напряжение 1,5 В, ее эквивалентное последовательное сопротивление составляет V4 Ом, а общий запас энергии равен приблизительно 10 ООО Вт о (постепенно эти характеристики ухудшаются; к концу срока службы батарейки напряжение может составлять около 1 В, а внутреннее сопротивление- несколько ом). О том, как создать источник напряжения с лучшими характеристиками, вы узнаете, когда мы изучим обратную связь. В электронных устройствах, за исключением портативных, батарейки используются редко.

1.05. Теорема об эквивалентном преобразовании источников (ге-иераторов)

Теорема об эквивалентном преобразовании источников утверждает, что всякую схему, состоящую из резисторов и источников напряжения и имеющую два вывода, можно представить в виде эквивалентной схемы, состоящей из одного резистора R, последовательно подключенного к одному источнику напряжения U. Представьте, как это удобно. Вместо того чтобы разбираться с мешаниной батарей и резисторов,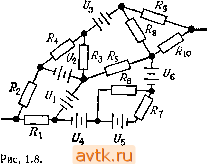

экв

можно взять одну батарею и один резистор (рис. 1.8). (Кстати, извест- иа еще одна теорема об эквивалентном преобразовании, которая содержит такое же утверждение относительно источника тока и параллельно подключенного резистора).

Как же определить эквивалентные параметры R и t/gB Для заданной схемы? Оказывается, просто, f/акв - это напряжение между выводами эквивалентной схемы в ее разомкнутом (ненагруженном) состоянии; поэтому, так как обе схемы работают одинаково, это напряжение совпадает с напряжением между выводами данной схемы в разомкнутом состоянии (его можно определить путем вычислений, если схема вам известна, или измерить, если схема неизвестна). После этого можно определить R, если учесть, что ток в эквизалентнон схеме

При условии что она замкнута (нагружена), равен UJHskb- Иными словами, 11у,р-=и (разомкнутая схема), Rb (разомкнутая схема) (замкнутая схема).

УНИВЕРСАЛЬНЫЕ ИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ

Существует немало приборов, с помощью которых в схемах можно измерять напряжения и токи. Самым универсальным из них является осциллограф (см. приложение А); он позволяет наблюдать изменение напряжения во времени в одной или нескольких точках схемы. Специально для отыскания неисправностей в цифровых схемах предназначены логические щупы и логические анализаторы. Универсальный измерительный прибор дает возможность измерять напряжение, ток и сопротивление очень часто с достаточно высокой точностью, однако у него медленная реакция, и он не может заменить осциллограф в тех случаях, когда интерес представляют меняющиеся напряжения. Универсальные измерительные приборы можно разделить на две группы: приборы, показания которых определяются по относительному перемещению стрелки, и более редкие цифровые приборы. Стандартный вольтомметр позволяет измерить ток по перемещению стрелки (обычно полный диапазон шкалы составляет 50 мкА). (Для того чтобы разобраться в работе измерительного прибора, советуем покопаться в книгах по электротехнике, но не в руководствах по разработке электронных схем; а пока нас вполне удовлетворит информация о том, что в приборе используются индуктивности и сердечники.) При измерении напряжения в вольтомметре последовательно к основной схеме подключается резистор. Например, диапазон шкалы измерения напряжения, равный 1 В, обеспечивается последовательным подключением резистора с сопротивлением 20 кОм к схеме, рассчитанной на ток 50 мкА; для больших диапазонов напряжения используются соответственно резисторы о большими сопротивлениями. Такой вольтомметр характеризуется как прибор на 20 ООО Ом/В. Это значит, что сопротивление его резистора, равное 20 кОм, умножается на полный размах напряжения в выбранном диапазоне измерения. Полный размах в любом диапазоне напряжения составляет 1/20 ООО В/Ом, или 50 мкА. Очевидно, что подобный вольтметр оказывает тем меньше влияния на схему, чем выше диапазон, так как играет роль резистора с большим сопротивлением (представим вольтметр в качестве нижнего плеча делителя напряжения, при этом верхнее плечо будет образовано эквивалентным выходным сопротивлением схемы, к которой подключен прибор). В идеальном случае вольтметр должен обладать бесконечным входным сопротивлением.

В настоящее время применяются разнообразные измерительные приборы с небольшим усилением, входное сопротивление которых может достигать 10 Ом. К приборам такого типа относятся большинство цифровых измерительных приборов и даже некоторые приборы с аналоговым отсчетом на полевых транзисторах (см. гл. 6). Замечание: иногда входное сопротивление измерительных приборов со входом на полевом транзисторе может быть очень большим в наиболее чувствительном диапазоне, а в других диапазонах оно может иметь меньшее значение. Например, типичными являются следующие значения: 10° Ом для диапазонов 0,2 В и 2 В и 10 Ом для всех остальных Диапазонов. Внимательно изучайте характеристики приборов! Для работы с транзисторными схемами подходит вольтомметр на 20 ООО Ом/В, который создает для них небольшую нагрузку. В любом случае нетрудно оценить влияние измерительного прибора на работу схемы, если воспользоваться уравнением для делителя напряжения. Обычно универсальные измерительные приборы имеют диапазоны измерения напряжения от I В (и меньше) до 1 кВ (и больше) для полного размаха шкалы.

С помощью вольтомметра можно измерять ток, оценивая его величину по простому отклонению указателя прибора (в предыдущем примере диапазон измерения тока составляет 50 мкА) или за счет резистора с небольшим сопротивлением, подключаемого параллельно основной схеме (шунта). Так как для перемещения указателя необходимо небольшое падение напряжения (обычно 0,25 В на полный размах шкалы), шунт выбирают при изготовлении прибора таким, чтобы максимальный ток вызывал соответствующее падение напряжения на параллельном соединении шунта и резистора измерительного прибора (для вас выбор шунта сводится к тому, что нужно лишь устано-

24 Г лапа 1

вить переключатель на нужный диапазон измерения). В идеальном случае прибор для измерения тока должен иметь нулевое сопротивление, тогда при подключении его к схеме последовательно он не будет оказывать влияния на нее. На практике приходится мириться с падением напряжения, составляющим десятые доли вольта какдляволь-томметров, так и для цифровых приборов. Обычно универсальные измерительные приборы имеют диапазоны измерения тока от 50 мкА (или ниже) до 1 А (или выше) для Полного размаха шкалы.

В универсальных измерительных приборах имеется одна или несколько батарей для подачи питания при измерении сопротивлений. Измерение падения напряжения при протекании небольшого тока позволяет определять величину сопротивления; предусмотренные для этих измерений диапазоны перекрывают величины сопротивления от 1 Ом (или ниже) до 10 .МОм (или выше). Замечание: не пытайтесь измерить ток источника напряжения путем подключения прибора к штепсельной розетке в стене; то же самое можно сказать об измерении сопротивления. Подобные измерения служат причиной гпбели многих приборов.

Упражнение 1.7. Что покажет вольтметр на 20 ООО Ом/В при шкале диапазона 1 В, если его подключить к источнику напряжения 1 В с внутренним сопротивлением 10 кОм? Что покажет этот прибор, если его подключить к делителю напряжения с плечами 10 кОм - 10 кОм, питающемуся от источника постоянного напряжения (с нулевым Сопротивлением) с напряжением 1 В?

Упражнение 1.8. Измерительный прибор с максимальным отклонением указателя, соответствующим току 50 мкА, имеет внутреннее сопротивление, равное 5 кОм. Какое шунтирующее сопротивление нужно подключить, чтобы прибор измерял ток в пределах О-1 А? Какое сопротивление нужно подключить последовательно для того, чтобы прибор мог измерить напряжение в пределах 0-10 В?

Попробуем применить описанный метод к делителю напряжения, для чего составим его эквивалентную схему:

1. Напряжение при разомкнутой цепи: U-UJiR2l{Ri+Ri)].

2. Ток замкнутой накоротко цепи: UjRi.

Тогда эквивалентная схема представляет собой источник напряжения /экв=вх [2/(1+2)], к которому последовательно подключен резистор с сопротивлением R=RiR2/{R1+R2). Не случайно сопротивление равно сопротивлению параллельно соединенных

резисторов и ;?2-(Объясне-

р-1 гЧ нне этому факту будет дано

1 экв ниже.)

J Узц Приведенный пример по-

казывает, что делитель на-н пряжения не может служить

i хорошей батареей, так как его

~ ~ выходное напряжение суш,ест-

венно уменьшается при подключении нагрузки. Рассмотрим упражнение 1.9. Вам сейчас известно все, что необходимо для того, чтобы точно рассчитать, насколько уменьшится выходное напряжение, если подключить к схеме нагрузку с определенным сопротивлением. Воспользуйтесь эквивалентной схемой, подключите нагрузку и подсчитайте новое выходное напряжение, учитывая, что новая схема представляет собой не что иное, как делитель напряжения (рис. 1.9).

Упражнение 1.9. Для схемы, показанном на рис. 1.9., L x=30 B,/?i=/?2=10 кОм. Требуется определить: а) выходное напряжение в отсутствие нагрузки (напряжение

разомкнутой цепи); б) выходное напряжение при условии, что подключена нагрузка 10 кОм (представьте схему в виде делителя напряжения, и /?н объедините в один резистор); в) эквивалентную схему; г) выходное напряжение при том же условии, что и в п. б , но для эквивалентной схемы здесь придется иметь д£ло с делителем напряжения; ответ должен быть такиь[ же, как в п. б ; д) мошдоеть, рассеиваемую каждым резистором.

Эквивалентное сопротивление источника и нагрузка схемы. Как мы только что убедились, делитель напряжения, на который подается некоторое постоянное напрялсение, эквивалентен некоторому источнику напряжения с последовательно подключенным к нему резне- тором. Подключение резистора в качестве нагрузки вызывает падение напряжения на выходе делителя, обусловленное наличием некоторого сопротивления источника (вспомним эквивалентное сопротивление для, делителя напряжения, если его выход выступает в качестве источника напряжения). Очень часто это явление нежелательно. Один подход к решению проблемы создания устойчивого источника напряжения (называемого устойчивым в том смысле, что он не поддается действию нагрузки) состоит в использовании в делителе напряжения резисторов с малыми сопротивлениями. Иногда этот прямой подход оказывается полезным. Однако лучше всего для создания источника напряжения, или как его часто называют, источника питания, использовать активные компоненты, такие, как транзисторы или операционные усилители. Этот подход позволяет создать источник напряжения, внутреннее сопротивление которого (или эквивалентное сопротивление) составит миллиомы (тысячные доли ома), при этом не требуются большие токи и не рассеивается значительная мощность, что характерно для низкоомного делителя напряжения с такими л<е рабочими характеристиками. Кроме того, в активном источнике питания не представляет труда регулировка выходного напряжения.

Понятие эквивалентного внутреннего сопротивления применимо ко всем типам источников, а не только к батареям и делителям напряжения. Все источники сигналов (например, генераторы синусоидальных сигналов, усилители и измерительные приборы) обладаютэк-вивалентным внутренним сопротивлением. Подключение нагрузки, сопротивление которой меньше или даже сравнимо с внутренним сопротивлением, вызывает значительное уменьшение выходного параметра. Нежелательное уменьшение напряжения (или сигнала) разомкнутой цепи за счет подключения нагрузки называется перегрузкой цепи . В связи с этим следует стремиться к тому, чтобы выполнялось условие ?я утр, так как высокоомная нагрузка оказывает небольшое ослабляющее влияние на источник; примеры тому вы встретите в последующих главах. Условие высокоомности является обязательным для таких измерительных приборов, как вольтметры и осциллографы. (Есть и исключения из этого общего правила; например, когда речь пойдет о линиях передач на радиочастотах, вы узнаете, что следует согласовывать импедансы для предотвращения отражений и потерь энергии.)

26 Глаза 1 ,

Несколько слов о принятых выражениях: часто можно услышать сопротивление со стороны входа делителя напряжения или нагрузка со стороны выхода составляет столько-то ом , Советуем принять эти обороты на вооружение, так как они в понятной форме указывают, где, по отношению к схеме, находится резистор.

Преобразование энергии. Задумайтесь над таким интересным вопросом; каким должно быть сопротивление нагрузки, чтобы при данном сопротивлении источника ей была передана максимальная мощность? (Термины сопротивление источника , внутреннее сопротивление и эквивалентное сопротивление относятся к одному и тому же сопротивлению.) Нетрудно заметить, что при выполнении условий R=Q и R =oo, переданная мощность равна нулю. Условие Ra=0 означает, что t/ =0, а I UjRg и поэтому P =UJ =0. Условие R =oo означает, что U =U и / =0, поэтому Рп=0. Максимум заключен, следовательно, между О и оо.

Упражнение 1.10. Докажите, что при выполнении условия Ra=Ra мощность в нагрузке максимальна для данного сопротивления источника. Замечание: пропустите 9X0 упражнение, если вы не знаете дифференциального исчислецня, и примите на веру, что приведенное здесь утверждение справедливо.

Чтобы Приведенный пример не вызвал у вас неправильного впечатления, хотим еще раз подчеркнуть, что обычно схемы проектируют таким образом, чтобы сопротивление нагрузки было значительно больше, чем внутреннее сопротивление источника сигнала, работающего на эту нагрузку.

1.06. Динамическое сопротивление

Часто приходится иметь дело с электронными устройствами, в которых ток / непропорционален напряжению U;q подобных случаях нет смысла говорить о сопротивлении, так как отношение U/I не является постоянной величиной, независимой от U, а, наоборот, зависит от и. Для подобных устройств полезно знать наклон зависимости и-/ (вольт-амперной характеристики). Иными словами, представляет интерес отношение небольшого изменения приложенного напряжения к соответствующему изменению тока через схему: Л(У/А/ (или dill l/dl). Это отношение измеряется в единицах сопротивления (в омах) и во многих расчетах играет роль сопротивления. Оно называется сопротивлением для малых сигналов, дифференциальным сопротивлением, динамическим или инкрементным сопротивлением.

Зенеровские диоды (стабилитроны). В качестве примера рассмотрим зенеровский диод (стабилитрон), вольт-амперная характеристика которого приведена на рис. 1.10. Зенеровские диоды используют для получения постоянного напряжения на каком-либо участке

РеапГ ный

тшлт] шрон /

Идеальный - стабилитрон

[ДиоЭ открыт

схемы*. Это достигается за счет тока (в грубом приближении постоянного), получаемого от источника большего напряжения в той же схеме. Важно понять, как будет вести себя соответствующее напряжение на зенеровском диоде (зенеровское напряжение пробоя) при изменении питающего тока; это изменение есть мера влияния изменений питающего тока. Оно характеризуется динамическим сопротивлением зенеров-ского диода, определяемым при заданном токе. (Учтите, что динамическое сопротивление зенеровского диода в режиме стабилизации изменяется обратно пропорционально току. Например, динамическое сопротивление зенеровского диода, создающего напряжение стабилизации 5 В, может быть равно 10 Ом при токе 10 мА. Воспользовавшись определением динамического сопротивления, найдем, чему будет равно изменение напряжения при изменении питающего тока на 10% 5 Д^=дипД=10-0,1-0,001 = 10 мВ или Af;/f;=0,002 = 0,2%. Тем самым подтверждаются высокие стабилизирующие качества зенеровского диода. На практике часто приходится иметь дело с такими схемами, как показанная на рис. 1.11. Здесь ток, протекающий через стабилитрон и резистор, обусловлен имеющимся в той же схеме напря жением, большим чем напряжение стабилизации. При этом /=а =(t/3x-tBHx) ? И А/=(Д^/ -АУ ) ?, тогда Л^/з =/? Л/=.

Рис. 1.10.

{RJR) (Д^вх-Д^вых) и, наконец.

UVR,J{R-\-R дии/<

Рис. 1,11.

Следовательно, по отношению к изменениям напряжения схема ведет себя как делитель напряжения, в котором зенеровский диод заменен резистором, сопротивление которого равно динамическому сопротивлению диода при рабочем токе. Приведенный пример показывает, для чего нужен такой параметр, как динамическое сопротивление. Допустим, что в рассмотренной нами схеме входное напряжение изменяется в пределах от 15 до 20 В, а для получения стабильного источника напряжения 5,1 В используется зенеровский диод типа 1NA733 (зенеровский диод с напряжением 5,1 В и мощностью 1 Вт). Резистор сопротивлением 300 Ом обеспечит максимальный зенеровский ток, равный 50 мА: (20-5,1)/300. Оценим изменение выходного напряжения,

1> Для стабилизации напряжения здесь используется участок пробоя на обратной ветви характеристики; этот (зенеровский) пробой не выводит диод из строя, если jOK ограничен,- Прим, ред.

зная, что максимальное сопротивление для выбранного диода составляет 7 Ом при токе 50 мА. В диапазоне изменения входного напряжения ток через зенеровский диод изменяется от 50 мА до 33 мА; изменение тока на 17 мА вызывает изменение напряжения на выходе схемы, равное Аи=/?д„ А/, или 0,12 В. Другие примеры использования зе-неровских диодов можно найти в разд. 2.04 и 5.13.

В реальных условиях зенеровский диод обеспечивает наивысшую стабильность, если он питается от источника тока, у которого по определению /?ди11=°° ( к не зависит от напряжения). Но источник тока представляет собой достаточно сложное устройство, и поэтому на практике мы чаще всего удовлетворяемся простым резистором.

Туннельные диоды. Еще один интересный пример использования параметра динамического сопротивления связан с туннельным диодом. Его вольт-амперная характеристика показана на рис. 1.12.

В области между точками Л и 5 он обладает отрицательным динамическим сопротивлением. Из этого вытекает важное следствие: делитель напряжения, состоящий из резистора и туннельного диода, может работать как усилитель (рис. 1.13). Воспользуемся уравнением для делителя напряжения и для изменяющегося напряжения i/сиги получим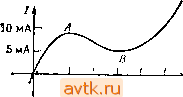

0,1 0,2 0,3 0,4 о; 5

Рис, 1.12.

Туннельный

Рис, 1.13.

/? и.

ВЫХ

где Г( - динамическое сопротивление туннельного диода при рабочем токе, t/c r - изменение малого сигнала, которое до настоящего момента мы обозначали через U , (в дальнейшем мы будем пользоваться этим широко распространенным обозначением). Для туннельного диода *дип<0. Значит, MJ/AKO или и/1<0 для области вольт-амперной характеристики туннельного диода, заключенной между точками А и В. Если г, ди <0, то знаменатель становится близким к нулю и схема начинает работать как усилитель. Напряжение У^аг создает пмтоянный ток, или смещение, которое смещает рабочую точку в об-./.асть отрицательного сопротивления. (Безусловно, во всяком усилительном приборе необходимо иметь источник питания.)

И наконец, в двух словах история туннельных диодов: они появились в конце 50-х годов, и с ними сразу стали связывать пути разрешения множества проблем схемотехники. Их высокое быстродействие дало основание предположить, что они произведут революцию в области вычислительной техники. К сожалению, оказалось, что эти эле-

менты сложны в использовании; это обстоятельство, а также успешное развитие транзисторов привело к тому, что туннельные диоды сейчас почти не находят применения.

Позже, при рассмотрении активных фильтров, мы вернемся к явлению отрицательного сопротивления. Тогда вы познакомитесь со схемой преобразователя отрицательного импеданса, которая обеспечивает наряду с другими характеристиками настоящее (а не динамическое) отрицательное сопротивление.

СИГНАЛЫ

Следующий раздел главы посвящен конденсаторам - элементам, свойства которых зависят от того, как изменяются в схеме напряжения и токи. Закономерности, с которыми мы познакомили вас при изучении цепей постоянного тока (закон Ома, эквиваленгные преобразования схем и др.), сохраняют свою силу и в тех случаях, когда напряжения и токи изменяются во времени. Для лучшего понимания работы цепей переменного тока полезно изучить некоторые распространенные типы сигналов (напряжений, которые определенньш образом изменяются во времени).

1,07. Синусоидальные сигналы

Синусоидальные сигналы распространены наиболее широко; если вы услышите выражение 10 мкВ на частоте 1 МГц , то знайте, что речь идет о синусоидальном сигнале. Математическое выражение, описывающее синусоидальное напряжение, имеет вид

и-=А sin 2 nft,

где А - амплитуда сигнала, / - частота в циклах в секунду, или в герцах. Синусоидальный сигнал показан на рис. 1.14. Иногда бывает полезно переместить начало коор-динат (/=0) в точку, соответствующую произвольному моменту времени; в этом случае в выражение для синусоидального напряжения следует включить фазу

и=А 81п(2п +ф).

Можно также воспользоваться понятием угловая частота и переписать выражение для синусоидального сигнала в другом виде:

(/=Л sin (о/,

где (О - угловая частота в радианах в 1 с. Если вы вспомните, что (о=2л/, то все станет на свои места.

Основное достоинство синусоидальной функции (а также основная причина столь широкого распространения синусоидальных сиг-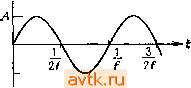

налов) состоит в том, что эта функция является решением целого ряда линейных дифференциальных уравнений, описывающих как физические явления, так и свойства линейных цепей. Линейная цепь обладает следующим свойством: выходной сигнал, порожденный суммой двух входных сигналов, равен сумме двух выходных сигналов, каждый из которых порожден входными сигналами, действующими не в совокупности, а отдельно; иначе говоря, если Вых. (А) - выходной сигнал, порожденный сигналом А, то для линейной цепи справедливо следующее равенство: Вых. {к-]гЪ)=Вых. {к)+Вых. (В). Если на входе линейной цепи действует синусоидальный сигнал, то на выходе также получим синусоидальный сигнал, но в общем случае его амплитуда и фаза будут другими. Это утверждение справедливо только для синусоидального сигнала. На практике принято оценивать поведение схемы по ее амплитудно-частотной характеристике, показывающей, как изменяется амплитуда синусоидального сигнала в зависимости от частоты. Усилитель звуковой частоты, например, имеет плоскую амплитудно-частотную характеристику в диапазоне от 20 Гц до 20 кГц.

Частота синусоидальных сигналов, с которыми чаще всего приходится работать, лежит в диапазоне от нескольких герц до нескольких мегагерц. Для получения очень низких частот, от 0,0001 Гц и ниже, достаточно аккуратно построить нужную схему. Получение более высоких частот, например до 2000 МГц, также не вызывает принципиальных трудностей, но для сигналов такой частоты нужны специальные линии передач и специальные приемы передачи. Кроме того, здесь приходится иметь дело с микроволновыми сигналами, для которых не подходят привычные схемы, состоящие из отдельных элементов, соединенных между собой проводами, а нужны специальные волноводы.

1.08. Измерение амплитуды сигналов

Оказывается, амплитуду синусоидального сигнала (а также любого другого сигнала) можно оценивать не только как абсолютное максимальное его значение. Иногда пользуются понятием двойная амплитуда (амплитуда от пика до пика сигнала), которая, как нетрудно догадаться, равна удвоенной амплитуде. Иногда употребляют понятие эффективное значение, которое определяется следующим образом: (;эфф=(1/1/ 2)Л=0,707 Л или 2AIU2V2 (это соотношение справедливо только для синусоидальных сигналов; для других видов сигналов отношение двойной амплитуды к эффективному значению будет другим). Пусть вас не удивляет, что сигнал часто характеризуют эффективным значением; дело в том, что именно эффективное значение используется для определения мощности. В США напряжение в сети имеет эффективное значение 117 В и частоту 60 Гц. Амплитуда этого напряжения равна 165 В (двойная амплитуда составляет 330 В).

Измерение амплитуды в децибелах. Как сравнить амплитуды двух сигналов? Можно, например, сказать, что сигнал X в два раза