Электроника имеет короткую, но богатую событиями историю. Первый ее период связан с простейшими передатчиками ключевого действия и способными воспринимать их сигналы приемниками, которые появились в начале нашего века. Затем наступила эпоха вакуумных ламп, которая ознаменовала собой возможность претворения в жизнь самых смелых идей. Сейчас мы являемся свидетелями нового этапа развития электроники, связанного с появлением элементов на твердом теле и характеризующегося неиссякаемым потоком новых ошеломляющих достижений. Технология изготовления больших интегральных схем (БИС) дает возможность производить такие кристаллы кремния, на основе которых создают калькуляторы, вычислительные машины и даже говорящие машины со словарным запасом в несколько сотен слов. Развитие технологии сверхбольших интегральных схем открывает возможность создания еще более замечательных устройств.

Наверное, стоит сказать и о том, что в истории развития электроники наблюдается тенденция уменьшения стоимости устройств при увеличении объема их производства. Стоимость электронной микросхемы, например, постоянно уменьшается по отношению к единице ее первоначальной стоимости по мере совершенствования процесса производства (см. рис. 11.18). На самом деле зачастую панель управления и корпус прибора стоят дороже, чем его электронная часть.

Если вас заинтересовали успехи электроники и если у вас есть желание самостоятельно конструировать всевозможные хитроумные вещи, которые были бы надежны, недороги, просты и красивы, то эта книга - для вас. В ней мы попытались раскрыть предмет электроники, показать, как он интересен и в чем состоят его секреты.

Первую главу мы посвящаем изучению законов, практических правил и хитростей, составляющих в нашем понимании основу искусства электроники. Начинать всегда следует с самого начала, поэтому мы выясним, что такое напряжение, ток, мощность и из каких компонентов состоит электронная схема. На первых порах, пока вы не научитесь видеть, слышать, осязать и ощущать электричество, вам придется столкнуться с определенными абстрактными понятиями (их особенно много в гл. 1), а также увязать свои представления о них с показаниями таких визуальных приборов, как осциллографы и вольтметры. Первая глава содержит в себе много математики, больше, чем другие главы, несмотря на то что мы старались свести математические выклад-

ОСНОВЫ ЭЛЕКТРОНИКИ

ки к минимуму и хотели бы способствовать развитию интуитивного понимания построения и работы электронных схем.

Раз уж мы занялись основами электроники, нам следует прежде всего начать с так называемых активных схем (усилителей, генераторов, логических схем и т. п.), благодаря которым электроника и вызывает к себе такой интерес. Читатель, у которого уже есть некоторые знания по электронике, может эту главу пропустить. Она предназначена для тех, кто прежде электроникой никогда не занимался. Итак, приступим к делу.

НАПРЯЖЕНИЕ, ТОК И СОПРОТИВЛЕНИЕ 1.01. Напряжение и ток

Напряжение и ток- это количественные понятия, о которых следует помнить всегда, когда дело касается электронной схемы. Обычно они изменяются во времени, в противном случае работа схемы не представляет интереса.

Напряжение (условное обозначение: U, иногда Е). Напряжение между двумя точками - это энергия (или работа), которая затрачивается на перемещение единичного положительного заряда из точки с низким потенциалом з точку с высоким потенциалом (т. е. первая точка имеет более отрицательный потенциал по сравнению со второй). Иначе говоря, это энергия, которая высвобождается, когда единичный заряд сползает от высокого потенциала к низкому. Напряжение называют также разностью потенциалов или электродвижущей силой (э. д. с). Единицей измерения напряжения служит вольт. Обычно напряжение измеряют в вольтах (В), киловольтах (1 кВ=10 В), милливольтах (1 мВ=10~ В) или микровольтах (1 мкВ=10~ В) (см. раздел Приставки для образования кратных и дольных единиц измерения , мелким шрифтом). Для того чтобы переместить заряд величиной 1 кулон между точками, имеющими разность потенциалов величиной 1 вольт, необходимо совершить работу з 1 джоуль. (Кулон служит единицей измерения электрического заряда и равен заряду приблизительно 6-10 электронов.) Напряжение, измеряемое в на-новольтах (1 нВ = 10~ В) иливмегавольтах(1 МВЮ^В) встречается редко; вы убедитесь з этом, прочитав всю книгу.

Ток (условное обозначение: /). Ток - это скорость перемещения электрического заряда в точке. Единицей измерения тока служит ампер. Обычно ток измеряют в амперах (А), миллиамперах (1 мА= = 10~ А), микроамперах (1 мкА=10~А),наноа1Мперах (1нА=10~ А) и иногда в пикоамперах (1 пкА=10~* А). Ток величиной 1 ампер создается перемещением заряда величиной 1 кулон за время, равное 1 с. Условились считать, что ток в цепи протекает от точки с более положительным потенциалом к точке с более отрицательным потенциалом, хотя электрон перемещается в противоположном направлении.

Запомните: напряжение всегда измеряется между двумя точками схемы, ток всегда протекает через точку в схеме или через какой-либо элемент схемы.

Говорить напряжение в резисторе нельзя - это неграмотно. Однако часто говорят о напряжении в какой-либо точке схемы. При этом всегда подразумевают напряжение между этой точкой и землей , то есть такой точкой схемы, потенциал которой всем известен. Скоро вы привыкнете к такому способу измерения напряжения.

Напряжение создается путем воздействия на электрические заряды в таких устройствах, как батареи (электрохимические реакции), генераторы (взаимодействие магнитных сил), солнечные батареи (фотогальванический эффект энергии фотонов) и т. п. Ток мы получаем, прикладывая напряжение между точками схемы.

Здесь, пожалуй, может возникнуть вопрос: а что же такое напряжение и ток на самом деле, как они выглядят? Для того чтобы ответить на этот вопрос, лучше всего воспользоваться таким электронным прибором, как осциллограф. С его помощью можно наблюдать напряжение (а иногда и ток) как функцию, изменяющуюся во времени. Мы будем прибегать к показаниям осциллографов, а также вольтметров для характеристики сигналов. Для начала советуем посмотреть приложение А, в котором идет речь об осциллографе, и раздел Универсальные измерительные приборы , мелким шрифтом.

В реальных схемах мы соединяем элементы между собой с помощью проводов, металлических проводников, каждый из которых в каждой своей точке обладает одним и тем же напряжением (по отношению, скажем, к земле). В области высоких частот или низких полных сопротивлений это утверждение не совсем справедливо, и в свое время мы обсудим этот вопрос. Сейчас же примем это допущение на веру. Мы упомянули об этом для того, чтобы вы поняли, что реальная схема не обязательно должна выглядеть как ее схематическое изображение, так как провода можно соединять по-разному.

Запомните несколько простых правил, касающихся тока и напряжения:

1. Сумма токов, втекающих в точку, равна сумме токов, вытекающих из нее (сохранение заряда). Иногда это правило называют законом Кирхгофа для токов. Инженеры любят называть такую точку схемы

Рис. 1.1.

узлом. Из этого правила вытекает следствие: в последовательной цепи (представляющей собой группу элементов, имеющих по два конца и соединенных этими концами один с другим) ток во всех точках одинаков.

2, При параллельном соединении элементов (рис. 1.1) напряжение на каждом из элементов одинаково. Иначе говоря, сумма падений на-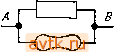

Рис. 1,2.

зависит от деформации) и т. д. Постепенно мы познакомимся с некоторыми экзотическими представителями этой плеяды; а сейчас рассмотрим самый нехитрый и наиболее распространенный элемент - резистор (рис. 1.2).

пряжения между точками А и В, измеренная по любой ветви схемы, соединяющей эти точки, одинакова и равна напряжению между точками А и В. Иногда это правило формулируется так: сумма падений напряжения в любом замкнутом контуре схемы равна нулю. Это закон Кирхгофа для напряжений.

3. Мощность (работа, совершенная за единицу времени), потребляемая схемой, определяется следующим образом:

PUI.

Вспомним, как мы определили напряжение и ток, и получим, что мощность равна: (работа/заряд)-(заряд/ед. времени). Если напряжение О измерено в вольтах, а ток / - в амперах, то мощность Р будет выражена в ваттах. Мощность величиной 1 ватт - это работа в 1 джоуль, совершенная за 1 с (1 Вт=1 Д^с).

Мощность рассеивается в виде тепла (как правило) или иногда затрачивается на механическую работу (моторы), переходит в энергию излучения (лампы, иередатчики) или накапливается (батареи, конденсаторы). При разработке сложной системы одним из основных является вопрос определения ее тепловой нагрузки (возьмем, например, вычислительную машину, в которой побочным продуктом нескольких страниц результатов решения задачи становятся многие киловатты электрической энергии, рассеиваемой в пространство в виде тепла).

В дальнейшем при изучении периодически изменяющихся токов и напряжений мы обобщим простое выражение P=UI. В таком виде оно справедливо для определения мгновенного значения мощности.

Кстати, запомните, что не нужно называть ток силой тока - это неграмотно. Нельзя также называть резистор сопротивлением. О резисторах речь пойдет в следующем разделе.

1.02. Взаимосвязь напряжения и тока: резисторы

Тема эта очень обширна и интересна. В ней заключена суть электроники. Если попытаться изложить ее в двух словах, то она посвящена тому, как можно сделать элемент, имеющий ту или иную характеристику, выраженную определенной зависимостью между током и напряжением, и как его использовать в схеме. Примерами таких элементов служат резисторы (ток прямо пропорционален напряжению), конденсаторы (ток пропорционален скорости изменения напряжения), диоды (ток протекает только в одном направлении), термисторы (сопротивление зависит от температуры), тензорезисторы (сопротивление

ПРИСТАВКИ ДЛЯ ОБРАЗОВАНИЯ КРАТНЫХ И ДОЛЬНЫХ ЕДИНИЦ ИЗМЕРЕНИЯ

Следующие приставки приняты для образования кратных и дольных единиц измерения в научной и инженерной практике:

109 108

103 10-3 10-е 10-

10-12 10-15

При сокращенном обозначении дольных единиц измерения соответствующая при- ставка и условное обозначение единицы пишутся слитно. Обратите внимание на использование прописных и строчных букв, особенно м и М в приставках и обозначениях единиц: 1 мВт - это 1 милливатт, или тысячная доля ватта; 1 МГц - это 1 миллион герц. Полные наименования единиц измерения всегда пишутся со строчной буквы, даже если они образованы от имен собственных. Полное наименование единицы измерения с приставкой также всегда пишется со строчной буквы. Прописные буквы используются для условных сокращений единиц измерения. Например: герц и килогерц, но Гц и кГц; ватт, милливатт н мегаватт, но Вт, мВт, и МВт,

Сопротивление и резисторы. Интересно, что ток, протекающий через металлический проводник (или другой материал, обладающий некоторой проводимостью), пропорционален напряжению, приложенному к проводнику. (Что касается провода, который используется в качестве проводников в схемах, то его обычно берут достаточно большого сечения, чтобы можно было пренебречь падениями напряжения, о которых мы говорили выше.) Это ни в коем случае не обязательно для всех случаев жизни. Например, ток, протекающий через неоновую лампу, представляет собой нелинейную функцию от приложенного напряжения (он сохраняет нулевое значение до критического значения напряжения, а в критической точке резко возрастает). То же самое можно сказать и о целой группе других элементов - диодах, транзисторах, лампах и др. Если вас интересует, почему металлические проводники ведут себя именно так, советуем прочитать курс физики Berkeley Phisics Course, том И, разд. 4.3-4.7 (см. библиографию). Резисторы изготавливают из проводящего материала (графита, тонкой металлической или графитовой пленки или провода, обладающего невысокой проводимостью). К каждому концу резистора прикреплен провод. Резистор характеризуется величиной сопротивления

R=UII;

сопротивление R измеряется в омах, если напряжение U выражено в вольтах, а ток / в амперах. Это соотношение носит название закон Ома . Резисторы наиболее распространенного типа-углеродистые

jg Г лат 1

композиционные - имеют сопротивление от 1 ома (1 Ом) до 22 мегаом (22 МОм). Резисторы характеризуются также мощностью, которую они рассеивают в пространство (наиболее распространены резисторы с мощностью рассеяния или Вт), и такими параметрами, как допуск (тддаость), температурный коэффициент, уровень шума, коэффициент напряжения (показывающий, в какой степени сопротивление зависит от приложенного напряжения), стабильность во времени, индуктивность и пр. Более подробную информацию о резисторах содержит раздел Резисторы , мелким шрифтом, а также приложения Б и Г в конце второго тома.

Грубо говоря, резисторы используются для преобразования напряжения в ток и наоборот. Этот вывод может показаться банальным, но скоро вы поймете, что имеется в виду.

Рис. 1.3.

Последовательное и параллельное соединение резисторов. Из определения сопротивления следует несколько выводов)

1. Сопротивление двух последовательно соединенных резисторов равно: R=Ri+Ri (рис. 1.3). При последовательном соединении резисторов всегда получаем большее сопротивление, чем сопротивление отдельного резистора.

2. Сопротивление двух параллельно соединенных резисторов (рис. 1.4) равно: R=RiRi/{Ri+Ri) или /?=l/(l/;?i+l ?г). При параллельном

Рис. 1.4,

соединении резисторов всегда получаем меньшее сопротивление, чем сопротивление отдельных резисторов. Сопротивление измеряется в омах (Ом). На практике, когда речь идет о резисторах с сопротивлением более 1000 Ом (1 кОм), иногда оставляют только приставку, опуская в обозначении Ом , т. е. резистор с сопротивлением 10 кОм иногда обозначают как 10 к, а резистор с сопротивлением 1 МОм - как 1 М. На схемах иногда опускают и обозначение Ом , оставляя только число. Может быть, все это кажется вам не очень интересным? Немного терпения, и мы перейдем к интересным практическим примерам.

РЕЗИСТОРЫ

Резисторы поистине вездесущи. Типы резисторов почти столь же многочисленны, как и схемы, в которых они применяются. Резисторы используются в усилителях, в качестве нагрузки для активных устройств, в схемах смещения и в качестве элементов обратной связи. Вместе с конденсаторами они используются для за-

Дания постоянной времени и работают как фильтры. Они служат для установки величии рабочих токов и уровней сигналов. В схемах питания резисторы используются для уменыиения напряжений за счет рассеяния мощности, для измерения токов и для разряда конденсаторов после снятия питания. В прецизионных схемах они помогают устанавливать нужные токи, обеспечивать точные коэффициенты пропорциональности для напряжения, устанавливать точные коэффициенты усиления. В логических схемах резисторы выступают в качестве оконечных эле-к(ентов линий и шнн, повышающих и понижающих элементов. В высоковольтных схемах резисторы служат для измерения напряжений, для выравнивания токов утечки через диоды или конденсаторы, соединенные последовательно. На радиочастотах они используются даже в качестве индуктивностей.

Промышленность выпускает резисторы с сопротивлением от 0,01 Ом до 102 Ом и мощностью от /в ДО 250 Вт с допуском от 0,005 до 20%. Резисторы изготавливают из графитовых смесей, металлических пленок, проводов, накрученных на каркас, или на основе полупроводниковых элементов, подобных полевым транзисторам. Наиболее распространены углеродистые композиционные резисторы, имеющие мощность А или 72 Вт. Существует стандартный диапазон значений сопротивлений-от 1 Ом до 100 МОм, причем для резисторов с допуском на сопротивление, равным 5%, выпускается в два раза больше значений сопротивлений, че.м для резисторов с допуском 10% (см. приложение В). Мы рекомендуем использовать резисторы фирмы Allen Brodley типа АВ (Д Вт, 5 %), так как они имеют понятную маркировку, стабильные характеристики и надежное соединение с проводниками выводов.

Резисторы настолько просты в обращении, что очень часто их принимают как нечто само собой разумеющееся. Между тем они не идеальны, и стоит обратить внимание на некоторые их недостатки. Возьмем, например, получившие широкое распространение резисторы композиционного типа с допуском 5%. Они хороши почти для любых схем с некритичными параметрами, но невысокая стабильность этих резисторов не позволяет использовать их в прецизионных схемах. Следует помнить об ограничениях, свойственных этим элементам, чтобы в один прекрасный день не оказаться разочарованны*!. Основной недостаток состоит в изменении сопротивления Во времени под действием температуры, напряжения, влажности. Другие недостатки связаны с индуктивными свойствами (они существенно сказываются на высоких частотах), с наличием термальных точек в мощных схемах или шумов в усилителях с низким уровнем шума. Ниже приводятся параметры резисторов в самых жестких условиях эксплуатации; обычно условия бывают лучше, по правильнее рассчитывать на худшее.

Характеристики резисторов фирмы Allen Bradley, серия АВ, тип СВ 2>

Стандартный допуск в номинальных условиях составляет 5%. Максимальная мощность при температуре окружающей среды 70°С составляет 0,25 Вт, при этом внутренняя температура повышается до 150°C. Максимальное приложенное напряжение составляет (0,25/?)/ или 250 В (меньшее из двух значений). Однократное превышение напряжения до 400 В в течение 5 с вызывает необратимое изменение сопротивления на 2%-

В схемах, где требуется высокая точность или стабильность, следует использовать резисторы из металлической пленки с допуском 17о (см. приложение Г). Они обеспечивают стабильность не хуже 0,1% в нормальных условиях и не хуже 1% в самых жестких условиях. Прецизионные проволочные резисторы способны удовлетворить наиболее высоким требования..

Если ожидается, что мощность, рассеиваемая в схеме, будет составлять более 0,1 Вт, то следует выбрать резистор с большим значением рассеиваемой мощности. Композиционные углеродистые резисторы характеризуются мощностью до 2 Вт, а мощные проволочные резисторы - более высокими значениями. Для мощ-

То есть точек локального перегрева. - Прим. ред.

> Примерно так же ведут себя отечественные резисторы МЛТ, Прим. ред.

Изменение сопротивления.

(R=l кОм) (;? = 1.0 МОм)

Необратимое?

Пайка (350 °С на расстоянии 3 мм) Циклическая нагрузка (50 циклов

ВКЛ/ВЫКЛ за 1000 ч) Вибрация (20 g) и удар (100 g) Влажность (95%-ная оти. влажнс

40 °С)

Коэффициент напряжения (изменение,

равное 10 В) Температура (от 25 до -15°С) Температура (от 25 до 85°С)

ажность при

ных схем наилучшие характеристики обеспечивает резистор с отводом тепла. Резисторы этого типа выпускаются с допуском 1 % и могут надежно работать при собственной температуре до 250°С в течение длительного периода времени.

Упражнение 1.1. Возьмем два резистора сопротивлением 5 и 10 кОм Чему равно сопротивление при (а) последовательном и (б) параллельном их соединении

Упражнение 1.2. Какую мощность будет рассеивать в пространство резистор с сопротивлением 1 Ом, подключенный к батарее автомобиля с напряжением 1 В'

Упражнение 1.3. Докажите справедливость формул для сопротивления последовательного и параллельного соединения резисторов.

Упражнение 1.4. Покажите, что сопротивление нескольких параллельно соединенных резисторов определяется следующим образом;

R==-

Секрет резисторов, соединенных параллельно: начинающие часто приступают к сложным алгебраическим выкладкам или углубляются в законы электроники, а здесь как раз лучше всего воспользоваться интуитивным правилом. Приступим теперь к освоению интуитивных правил и развитию интуиции.

Правило 1. Сопротивление двух резисторов, один из которых обладает большим сопротивлением, а другой малым, соединенных между собой последовательно (параллельно), приблизительно равно большему (меньшему) из двух сопротивлений.

Правило 2. Допустим, вы хотите узнать, чему равно сопротивление двух параллельно соединенных резисторов, обладающих сопротивлением 5 и 10 кОм. Если вообразить, что резистор сопротивлением 5 кОм представляет собой параллельное соединение двух резисторов сопротивлением 10 кОм,то схема будет представлена параллельным соединением трех резисторов с сопротивлением 10 кОм. Так как сопротивление одинаковых параллельно соединенных резисторов равно 1/п-й части сопротивления одного из них, то ответ в нашей задаче будет 10 кОм/3, или 3,33 кОм. Это правило полезно усвоить, так как с его помощью можно быстро проанализировать схему

в уме . Мы хотим, чтобы вы научились решать стоящие перед вами задачи, имея под рукой минимум - оборотную сторону почтового конверта и ручку. Тогда блестящие идеи, возникшие у вас в любой момент, не будут встречать препятствий на пути своего развития,

И еще несколько принципов нашей доморощенной философии: среди начинающих наблюдается тенденция вычислять значения сопротивлений резисторов и характеристики других компонентов схем с большой точностью, доступность же карманных калькуляторов в наше время помогает развитию этой тенденции. Поддаваться ей не следует по двум причинам: во-первых, компоненты сами по себе имеют определенную конечную точность (наиболее распространенные резисторы - ±5%; характеристики транзисторов, например, часто задаются одним-двумя коэффициентами); во-вторых, одним из признаков хорошей схемы является ее нечувствительность к точности величин компонентов (бывают, конечно, и исключения). И еще: вы скорее придете к интуитивному пониманию схем, если разовьете в себе способность быстро прикидывать в уме , а не будете увлекаться вычислениями с ненужной точностью на красивых калькуляторах.

Некоторые считают, что, для того чтобы скорее научиться оценивать величину сопротивления, полезно вводить понятие проводи^ мость, G = 1/R. Ток, протекающий через элемент с проводимостью G, к которому приложено напряжение U, определяется как / = GU, (это закон Ома). Чем меньше сопротивление проводника, тем больше его проводимость и тем больше ток, протекающий под воздействием напряжения, приложенного между концами проводника.

С этой точки зрения формула для определения сопротивления параллельно соединенных проводников вполне очевидна; если несколько резисторов или проводящих участков подключены к одному и тому же напряжению, то полный ток равен сумме токов, протекающих в отдельных ветвях. В связи с этим проводимость соединения равна сумме отдельных проводимостей составных элементов: G = Gi + G2-\- Ga+ а это выражение эквивалентно выражению для параллельно соединенных резисторов, приведенному выше.

Инженеры неравнодушны к обратным величинам, и в качестве единицы измерения проводимости они установили 1 сименс (1 См = 1/1 Ом), который иногда называют мо ( ом наоборот). Хотя понятие проводимости и помогает развить интуицию в отношении сопротивлений резисторов, широкого применения оно не находит, и большинство предпочитает иметь дело с величинами сопротивлений, а не проводимости.

Мощность и резисторы. Мощность, рассеиваемая резистором или любым другим элементом, определяется как Р = UI. Пользуясь законом Ома, эту формулу можно записать в другом видез Р = я;? или Р = U/R.

Упражнение 1.5. Возьмем схему, работающую от батареи с напряжением 15 В. Докажите, то независимо от того, как будет включен в схему резистор, обладающий сопротивлением более 1 кОм, мощность на нем не превысит U Вт.

Упражнение 1.6. Дополнительное упражнение: для Нью-Йорка требуется lOi Вт Э1ектрической энергии при напряжении 110 В (цифры вполне правдоподобны: 10 млн. жителей, каждый потребляет в среднем 1 кВт электроэнергии). Высоковольтный кабель может иметь диаметр 25,4 мч. Давайте подсчитаем, что произойдет, если в качестве кабеля взять провод из чистой меди диаметром 0,305 м. Сопротивление такого провода составляет 0,05 мкОм (5-10- Ом) в расчете на 0,305 м. Определите: а) потери мощности в расчете на 0,305 м, исходя из того, что потери оцениваются величиной PR; б) длину кабеля, на которой будут потеряны все 10Вт; в) если вы знаете физику, определите, до какой температуры нагреется кабель (а=6-10- Вт/(К*См)).

Если расчет выполнен правильно, то результат, вероятно, удивил вас. Как же разрешить проблему?

1.03. Делители напряжения

Резисторы находят самое широкое применение. Была бы схема, а делителей напряжения для нее можно придумать с полдюжины. На рис. 1.5. представлена простая схема. Что такое t/вых? Предположим здесь и далее, что нагрузки на выходе нет, тогда ток определяется следующим образом: I=U,J{Rx+R2). (Мы воспользовались формулой для определения сопротивления резистора и правилом для последовательного соединения рези-D сторон.) Тогда U =IR,U,JJ{R,-R2).

Обратите внимание, что выходное напря-

жение всегда меньше входного (или равно

\ ему); поэтому мы говорим о делителе напря-7?2 Удь,х жения. Если одно из сопротивлений будет от-I рицательным, то можно получить усиление i. (т. е. выходное напряжение будет больше вход-

р^,(. 1 5 ного). Эта идея не так невероятна, как кажет-

ся на первый взгляд: вполне можно сделать устройство с отрицательными приращениями сопротивления (в качестве примера может служить туннельный диод) или просто с настоящим отрицательным сопротивлением (например, преобразователь с отрицательным импедансом, о котором мы поговорим позже). Однако эти примеры достаточно специфичны и не должны занимать сейчас ваше внимание.

Делители напряжения часто используют в схемах для того, чтобы получить заданное напряжение из большего постоянного (или переменного) напряжения. Например, если в качестве R взять резистор с регулируемым сопротивлением, то мы получим не что иное, как схему с управляемым выходом. Простой делитель напряжения играет важную роль и в тот момент, когда вы задумываете схему: входное напряжение и сопротивление верхней части резистора могут представлять собой, скажем, выход усилителя, а сопротивление нижней части резистора - вход последующего каскада. В этом случае, воспользовавшись уравнением для делителя напряжения, можно определить, что поступит на вход последнего каскада. Все сказанное станет более , понятным, когда чуть позже мы познакомим вас с одним интересным