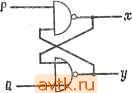Рис. 1.54. К упражнению 1.13.

1.14. а) Постройте таблицу состояний для цепи, изображенной на рис. 1.55, при условии, что все триггеры синхронные.

б) Постройте цепь по таблице состояний п. а), используя то же кодирование, но в качестве элементов памяти PS-триггеры.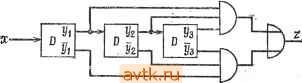

Рис. 1.55. К упражнению 1.14.

1.15. а) Постройте таблицу состояний для цепи, изображенной на рис. 1.56, при условии, что все триггеры синхронные.

б) Дайте словесное описание последовательностной функции, реализованной этой цепью.

1.16. Разработайте схему счетчика с двумя управляющими входами С, и Сг, в которой Cl определяет модуль счета и Cj - инкремент. Схема работает таким образом, что если Ci = о, счетчик считает по модулю 3, если Ci = О, счетчик считает по модулю 4. Если Сг = О, то на каждый такт счета прибавляется 1, если Сг = о, 1 вычитается.

1.17. а) Разработайте последовательностную цепь, реализующую умножитель на постоянное число, обладающий следующими свойствами: устройство должно иметь один вход х и один выход Z. Если вход интерпретируется как последовательное представление числа N (начиная с младших разрядов), то выходная последовательность должна иметь вид числа 2-N (начиная с младших разрядов).

3 Зак, 841

j, g л = о или 1, у®г = yz + yz (для каждого подмножества переменных XI, Хп существует один терм. Такое представление носит название представления Рида -Мюллера). Учтите, что Xi ф 1 ®

1.12. Докажите, что любую комбинационную функцию можно представить в виде

а) f {хх, Х2.....Хп) = xif (1 Х2, .... Хп) + xif ф,Х2, ..., Хп).

t) t{XuX2,..., Xn) = X\X2t{\, 1, Хъ, . . ., Хп) + XlXif (О, \, Xi, Хп) +

+ ХхЫ(у о, Xi, Хп) + XiXzfiO, о, Хз, .... Хп).

в) Обобщите это разложение на i переменных (это представление известно как разложение Шеннона).

1.13. На рис. 1.54 изображена схема, предлагаемая в качестве нового типа триггера. Постройте таблицу переходов этой схемы и оцените ее полезность по сравнению с D-, RS- и c-тpиггepaмн.

2п

Рис. 1.56. К упражнению 1.15.

сигналы образуют последовательность пяти символов с тремя единицами, двумя нулями и первые два символа в последовательности 11.

с

Рис. 1.57. К упражнению 1.19.

1.19. Постройте таблицу состояний для цепи, изображенной на рис. 1.57.

1.20. Постройте таблицу состояний для реализации цепи с одним входом х и одним выходом 2, работающей следующим образом. Начальное состояние {t = 0) равно 9о- Пусть U(Г) равно числу входов 1 за время от < = О до

б) Решите ту же задачу при условий, что на выходе реализуется последовательность 3-N.

1.18. Постройте диаграмму состояний автомата с одним входом х, одним выходом z при условии, что 2=1, если 4 предыдущих и текущий входные

Рис. 1.58. К упражнению 1.24.

1.25. Докажите или покажите на примере справедливость следующих утверждений:

а) Для каждой простой импликанты Р функции f(Xi.....Хп) существует

минимальная двухступенчатая реализация этой функции, содержащая Р.

б) Для комбинационной функции, не имеющей неопределенных элементов, существует единственное выражение минимальной суммы произведений.

в) Для комбинационной функции, не имеющей неопределенных элементов, стоимости минимальной суммы произведений и минимального произведения сумм равны.

г) Если комбинационная функция f{Xi, Хг, Хп) имеет единственное выражение минимальной суммы произведений, то она имеет также единственное выражение минимального произведения сумм и эти выражения имеют одинаковую стоимость.

1.26. Для каждой из нижеследующих функций постройте конечную таблицу состояний, ее реализующую, или докажите, что это сделать невозможно:

а) Выход автомата равен 1 тогда и только тогда, когда по меньшей мере 2 из 3 предыдущих входных символов были равны нулю.

б) Выход автомата в момент t равен 1 тогда и только тогда, когда для входной последовательности до момента t включительно число нечетных последовательностей единиц четное.

в) Выход автомата в момент t равен 1 тогда и только тогда, когда для входной последовательности до момента t включительно длина наибольшей последовательности нулей четная.

= Г, и V{T) - числу входов О за то же время. Выход Z{T) в момент времени Т должен равняться 1 тогда и только тогда, когда У (Г) -U{T) = 3k, где й -постоянное число (т. е. V{T) - U(T) ... -9, -6, -3, О, 3, 6, 9. ...).

1.21. Постройте таблицу состоянии синхронного последовательностного автомата на два входа Х\ к Х2 к два выхода 2i и z. Входная информация представляет собой двухразрядные числа щ, /is, поступающие последовательно, начиная с наибольшего значащего разряда. Выходная информация должна быть последовательным представлением 2i = max(/ii, и 22 = min(/ii, щ).

1.22. Какое максимальное число простых импликант может иметь комбинационная функция п переменных?

1.23. Функция f(x) является самодуальной, если функция fd, дуальная f, равна f (т. е. f = fd). Докажите, что число самодуальных функций п перемен-

ных равно

1.24. а) Для цепи, изображенной на рис. 1.58, f, = А+В, fg - логический элемент Я, Z = А. Является ли fz однозначно определенной?

Глава 2 КОМБИНАЦИОННЫЕ ЦЕПИ ИЗБРАННЫЕ ЗАДАЧИ

В гл. 1 были рассмотрены процедуры получения минимальных двухступенчатых реализаций комбинационных функций. В этой главе эти процедуры будут распространены на многовы-ходовые цепи для получения реализаций некоторых комбинационных функций, а также многоступенчатых реализаций комбинационных функций. Затем будут рассмотрены некоторые важные классы комбинационных функций, а именно: симметричные, юнатные и пороговые. Наконец, мы рассмотрим множества логических функций, которые могут быть использованы для реализации произвольных комбинационных функций.

2.1. КОМБИНАЦИОННЫЕ ЦЕПИ

С РАЗВЕТВЛЕННЫМ ВЫХОДОМ

При реализации нескольких комбинационных функций часто удается получить цепь с разветвленным выходом, требующую меньше логических элементов, или отдельные цепи, реализующие каждую из этих функций. Это достигается распределением логики среди участков цепи, реализующих различные функции. Такое распределение предполагает, что выход логического элемента может быть связан со входами более чем одного логического элемента. Число логических элементов, соединенных с выходом некоторого логического элемента, называется коэффициентом разветвления по выходу. Если этот коэффициент ограничен единицей, то задача получения минимальной двухступенчатой цепи для реализации множества функций не отличается от задачи реализации каждой индивидуальной функции минимальной двухступенчатой реализации. (Заметим, что коэффициент разветвления по выходу, больший единицы, может быть необходим даже при реализации индивидуальной функции.)

Для двухступенчатых цепей вида И-ИЛИ совместное использование логических элементов возможно только в случае, если не менее двух функций имеют общую импликанту. Поэтому концепция простых импликант должна быть обобщена так же на случай разветвленной логики. Это демонстрируется парой комбинационных функций, приведенных на рис. 2.1. На рис. 2.2 показана двухступенчатая реализация этих двух функций вида И-ИЛИ, минимизирующая общее число входов логических элементов. Из карт Карнау, изображенных на рис. 2.1, легко видеть, что терм X2XsXi не является простой импликантой ни fi, ни /г- Однако он представляет собой простую импликанту произве-

Рис. 2.1. Пара комбинационных функций.

бинационной цепи с разветвленным выходом и введения представления об импликанте для этой цепи [9] (или коротко - много-выходовой импликанте).

J4x-*xi*x

Рис. 2.2. Минимальная двухступенчатая реализация двух функций.

Пусть F = {/i, /г, .... /Л представляет собой множество комбинационных функций, а F - подмножество F. Терм-произведение Р называется простой многовыходовой импликантой подмножества F, если он является простой импликантой G = Щ' . hp

(произведение всех функций в F). Так как F может содержать одну функцию fi, то все простые импликанты отдельных функций

дения /г/г этих функций, как видно из рассмотрения карты Карнау, изображенной на рис. 2.3. Отсюда следует необходимость обобщения представления о простой импликанте на случай ком-

Рис. 2.3. Карта Карнау /i /г-

Доказательство. Рассмотрим минимальную двухступенчатую реализацию вида И-ИЛИ множества функций F = {fi, /г, ..., fr) и предположим, что выход А некоторого логического элемента И равен терм-произведению Р, не являющемуся простой многовыходовой импликантой.

Предположим также, что выход Л является входом логических элементов ИЛИ, реализующих подмножество комбинационных функций F = F. Тогда, поскольку Р не есть простая много-выходовая импликанта, должна существовать простая много-

выходовая импликанта Р' функции G - Uf, такая, что Р' по-

открывает каждую точку 1 функции fi е F, покрытую Р, каждая точка, покрытая Р', является точкой 1 или неопределенной точкой для каждой fiF и число литерал в Р' не превышает числа литерал в Р. Следовательно, мы можем заменить логический элемент А элементом А', который реализует простую многовыходовую импликанту Р', причем полученная при этом цель будет также являться минимальной двухступенчатой реализацией

также являются простыми многовыходовыми импликантами. Нижеследующая теорема доказывает возможность получения минимальных двухступенчатых реализаций вида И-ИЛИ множества комбинационных функций, в которых выход каждого логического элемента И представляет собой простую многовы-ходовую импликанту.

Теорема 2.1. Для множества комбинационных функций Р = {/i. /г, ..., /г) существует минимальная двухступенчатая реализация вида И-ИЛИ, в которой выход каждого логического элемента И представляет собой простую многовыходовую импликанту.

вида И-ИЛИ множества функций F. Аналогичным образом, можно заменить все элементы И, и выход каждого логического элемента И представляет собой простую многовыходовую им-пликанту.

Из сказанного следует, что задача обобщения минимальной двухступенчатой реализации вида И-ИЛИ на множество комбинационных функций может быть решена с помощью следующей процедуры.

Процедура 2.1

1. Получить множество всех простых многовыходовых импликант (при этом необходимо помнить, что простые импликанты отдельной функции fi также являются простыми многовыходо-выми импликантами).

2. Выбрать множество простых многовыходовых импликант минимальной стоимости для реализации множества комбинационных функций. Если выбирается простая многовыходовая импликанта множества функций Р s F, то она используется для реализации каждой fi F.

2.1.1 ПОЛУЧЕНИЕ ПРОСТЫХ МНОГОВЫХОДОВЫХ ИМПЛИКАНТ

Табличный метод получения простых импликант отдельных комбинационных функций (процедура 1.2) может быть распространен для получения простых многовыходовых импликант для множества функций F без точного вывода произведений всех подмножеств F.

Для указания, является ли каждый минтерм точкой 1 или точкой О для каждой из реализуемых функций, каждому мин-терму ставится в соответствие функциональный идентификатор. При объединении термов эта информация используется для определения подмножеств множества F, для которых результирующий терм является простой многовыходовой импликантой. Например, если /1 {xuXz, х^) = ХхХ^Хъ + 1X2:3, а /2 = х\Х2Хъ + + Х\Х2Хъ, то Х\Х2 не является простой многовыходовой импликантой {/ь/г}, так как Х1Х2Х3 не является точкой 1 /2, хотя он представляет собой простую импликанту fi.

Процедура 2.2

1. Образовать таблицу из всех точек 1 и неопределенных точек для полного множества функций Ц\, /г, /Л- Разделить это полное множество на множества 5о, 5i, ..., S , где множество Si содержит все такие точки с i переменными, равными 1. Прибавить к таблице множество из г столбцов, озаглавленных и, f% fj.. Эти столбцы будут использованы для каждой строки таблицы тех функций, для которых она является точкой 1 (или неопределенной точкой) и для которых она является точ-

) Используя такое обозначение, можно получить термы произведения, не покрытые ни одной точкой 1. Чтобы избежать этого, нужно использовать трехзначный функциональный идентификатор.

кой 0. Приписать каждой точке (Xj) в таблице в этих г столбцах функциональный идентификатор, равный 1 в столбце fu если /i(Xj) =7 О, и О в столбце fu если /j(Xj) ~ О

2. Строки этой таблицы будут слиты для образования множеств Si тем же способом, как для отдельных комбинационных функций (процедура 1.2). Когда строки Xj и Xj сливаются, в функциональном идентификаторе результирующей строки в столбце fk будет иметь место 1, только если fk{xi)ФQl и

В остальных случаях элемент в столбце f равен нулю. Если все г элементов функционального идентификатора равны нулю, то результат слияния не является простой многовыходовой импликантой, и строка может быть исключена из таблицы. Если результирующий функциональный идентификатор идентичен функциональному идентификатору х, (и/или х^), то строка Xj (и/или Xj) не является простой многовыходовой импликантой. Такая строка отмечается флажком (V)x,- (и/или Ху).

3. Продолжать объединение строк тем же способом до тех пор, пока это возможно. Строки, не отмеченные флажками, представляют собой простые многовыходовые импликанты, и соответствующее множество функций указывается функциональными идентификаторами.

Процедуру 2.2 можно распространить на термы, не покрывающие точки 1 какой-либо функции, так как функциональный идентификатор принимался равным 1 как для неопределенных точек, так и для точек 1 функции. Конечно, в процессе получения множества минимальных покрытий с помощью процедуры 2.1 минтермы будут отброшены. Вместо этого для точек О, 1 и неопределенных точек можно использовать трехзначные функциональные идентификаторы и процедуру, обобщенную для обеспечения идентификации импликант, не покрывающих какие-либо точки 1.

Пример 2.1. Рассмотрим функции f\ и /г (рис. 2.1). Таблица, образованная в соответствии с шагом (1) процедуры 2.2, показана на рис. 2.4, а. На рис. 2.4, б приведены результаты объединения строк таблицы на рис. 2.4, а, а на рис. 2.4, в - строк таблицы на рис. 2.4, б.

Простые многовыходовые импликанты и соответствующие функции (в круглых скобках) равны

XlXXiHi), XiXXsifz), XiX.2X{fi), XiXgXi (/2), XzXXi

if I /2),

X2X3 if l)X2Xi if 2).

3

Р4С. 2.4. Табличный способ нахождения мняговыходовых простых импликант.

Рис. 2.5. Две комбинационные функции {а); таблица для нахождения много-выходовых простых импликант (б).

простая многовыходовая импликанта для FF, то она является также простой многовыходовой импликантой для F с F, если не имеется другой простой импликанты Pj, покрывающей все точки 1 функции е F , покрытые Р и содержащей меньше литерал. Следовательно, установить, является ли простая многовыходовая импликанта подмножества F также простой многовыходовой импликантой подмножества F , можно проверкой всех таких импликант всех множеств F* cz F.

Пример 2.2. Для пары комбинационных функций, показанных на рис. 2.5, а, процедура 2.2 ведет к таблице, изображенной

Процедура 2.2 позволяет получить все простые многовыходовые импликанты множества функций F = {fi, /2, . , /г}, за следующим исключением. Она не учитывает, что простая много-выходовая импликанта подмножества F множества F может также быть простой многовыходовой импликантой подмножества F czF. При процедуре 2.2 только одна строка соответствует этой простой импликанте, а связанный с ней функциональный идентификатор соответствует F. Вообще если Pj -