На рис. 8.8 показана реализация пересечения двух проводников на основе магнитных доменов. Эта схема должна запускаться (циркуляционным) доменом, циркулирующим по позициям, находящимся на пересечении двух показанных на рисунке путей. Прибытие домена со стороны Лвх заставит циркуляционный домен продвинуться по пути, ведущему к Лвых, и уступить свое место вновь прибывшему домену. Если домен прибывает со стороны Ввх, то он заставляет циркуляционный домен двигаться по пути к Ввых, уступив циркуляционную позицию прибывшему домену. Какой из доменов останется в циркуляционной позиции, если оба пути Л и В содержат домены, зависит от относительных временных соотношений их движения по путям Л и В, но в любом случае перемещение доменов происходит по направлению к ячейкам Лвых и Ввых.

8.3. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ВЗАИМОДЕЙСТВИЯ ЦМД

В порядке изучения свойств логических элементов, работающих на магнитных доменах, удобно рассмотреть математическую модель взаимодействия ЦМД, построенную с учетом рассмотренных основных физических свойств ЦМД. Предполагается, что существует множество вершин V, представляющих собой множество возможных ячеек, в которых могут находиться ЦМД, и что любую пару вершин из множества V можно заставить взаимодействовать. (На практике взаимодействовать могут только соседние ЦМД. В этой главе далее будут рассмотрены задачи, учитывающие это ограничение. Упрощающее предположение вводится исключительно для получения некоторых предварительных результатов, не зависящих от указанного ограничения.) Рассмотрим сначала простейшее действие, а именно передачу ЦМД из вершины Л в вершину В. При этом подразумевается, что перемещением отдельных ЦМД можно управлять так же, как это делается в рассмотренном в разд. 8.2 методе, основанном на использовании проводящих петель.

Для того чтобы передвинуть ЦМД из вершины Л в вершину В, мы прикладываем к вершине В соответствующее магнитное поле, а на все соседние вершины, за исключением вершины Л, накладываем компенсирующее поле. ЦМД переместится из вершины Л в В тогда и только тогда, когда ЦМД содержит только вершина Л. Обозначим такое взаимодействие между Л и В через е = (Л, В) и будем называть его передачей ЦМД [13]. В нашей математической модели считается, как указывалось выше, что вершины А и В могут быть произвольными, хотя на практике при передаче ЦМД эти вершины должны быть смежными

Рис. 8.9. Представление переменной двумя позициями (ячейками).

ЦМД перемещались из своих ячеек, а в пустых ячейках появлялись ЦМД. Поскольку это нельзя выполнить на основе одних только передач ЦМД, оказывается удобным представлять переменную двумя ячейками вместо одной. Это показано на рис. 8.9. Здесь две ячейки Ai и .4о используются для представления одного значения логической переменной а. Наличие ЦМД в ячейке Ль но не в ячейке Ло соответствует а= I, наличие ЦМД в ячейке Ло, но не в ячейке Ai соответствует а = 0. Таким образом оба логических значения и О и 1 выражаются в наличии ЦМД и нет необходимости при отсутствии ЦМД в ячейке Ai созда вать ЦМД в ячейке Ло и наоборот. При этом для представле ния п двоичных переменных требуется 2п ячеек. (Если 2 воз

(с тем же успехом можно предположить, что все пары вершин в математической модели являются смежными).

Пусть XV обозначает множество вершин, первоначально содержащих ЦМД, а -множество ячеек, содержащих ЦМД после передачи е = (Л, В). Тогда

Х'(Х-{А})[]{В), если А^Х и ВфХ,

и .

Х' = Х в противном случае.

Такое взаимодействие будем называть командой, а последовательность команд - программой [13].

Пусть а*и b являются двоичными переменными, которые представляют исходное состояние ячеек Л и fi (т. е. а= 1, если Л содержит ЦМД, и а = О, если Л не содержит ЦМД), и пусть а' и Ь' являются двоичными переменными, которые представляют состояние этих ячеек после взаимодействия е= {А, В). Тогда

а' = а-Ь, Ь' = а + Ь.

Следовательно, передачу ЦМД можно использовать для выполнения операций логическое И и логическое ИЛИ.

Для образования дополнения необходимо, чтобы в результате выполнения одной последовательности команд существующие

ние т и k таково, что

(Г)> ->

Если для представления каждой переменной используются две ячейки, то, используя не содержащую ЦМД ячейку В, с помощью следующей программы можно получить дополнение переменной:

Р = 6,6263,

где

ei = (.4b fi); е2 = (Ло, ЛО и ез = (Б, Ло).

После работы этой программы содержимое обеих ячеек определяется в виде

аГ = о и < = о„

где йг представляет содержимое ячейки Л г, г = О, 1.

Поскольку мы показали, что все логические операции И, ИЛИ, НЕ можно реализовать на основе передачи ЦМД. можно сделать предположение о том, что все комбинационные функции могут быть реализованы при помощи передачи ЦМД, так как И, ИЛИ и НЕ представляют полное множество простейших логических элементов. Однако традиционные методы реализации предполагают, что разветвление по выходу может быть осуществлено. Мы еще не показали, что это возможно в раМках рассматриваемой нами математической модели взаимодействия магнитных доменов. Теперь мы докажем, что на самом деле разветвление по выходу невозможно при использовании только передачи ЦМД. В этой связи нам понадобятся следующие предварительные результаты. Пусть X s У и F s У представляют два множества ячеек, которые содержат ЦМД. Число общих для X и Y ячеек, т.е. ХГ1У|, называется перекрытием этих двух множеств.

Лемма 8.1. Если е= {А,В) и X, YV представляют два множества ячеек, которые содержат в исходный момент ЦМД, то

Доказательство. Команда е = (Л, В) не изменяет содержимого ячейки С Ф А, В. Следовательно, достаточно рассмотреть перекрытие в ячейках Л и б до и после выполнения команды е.

можных комбинаций из п переменных кодируются кодом k - m - m, т.е. кодом, в котором при любой входной комбинации ровно k из т переменных равны 1, то любую логическую функцию можно реализовать без использования инверторов. В таком коде для представления всех возможных входных комбинаций существенными являются только т ячеек, а соотноше-

перекрытие=z

Рис. 8.10. Иллюстрация к доказательству теоремы 8.2.

Доказательство. Рассмотрим два множества X, Fez У, такие, что y - X - {А}. Пусть существует дублирующая программа Р. Если X и F представляют множества ячеек, первоначально занятых ЦМД, то, поскольку X и F отличаются в одной ячейке, Х-Р и F отличаются в двух ячейках, одной в оригинале и одной в копии. Это противоречит теореме 8.1. Отсюда следует, что дублирующей программы не существует.

На рис. 8.10 приводится иллюстрация к доказательству при \V\ =8, [Х] =4, ]F =3. В yp один ЦМД займет любую из четырех ячеек вне Xi и Хг. Заметим, что, хотя общее число ЦМД до и после выполнения программы остается одинаковым, теорема 8.1 не удовлетворяется и, следовательно, такой программы не существует.

Для ИСХОДНЫХ множеств X и y существуют по четыре возможных комбинации исходных состояний ячеек А и В. Вычисление перекрытий в каждом из 16 возможных случаев до и после выполнения команды е - {А, В) доказывает лемму.

Теорема8.1. {теорема о Не Уменьшающемся Перекрытии [13]).

Для всех программ Р = ех, eg, ...,е„ и всех X, y , \xpyp\>\X{\y\.

Доказательство. Непосредственно следует из леммы 8.1.

Пусть Уь Уг сг У, Vi П Уг = Ф, и пусть XiVi и Хг Уа определяют расположение ЦМД. Хг называется копией Х\, если между элементами множества Xi и элементами множества Хг существует взаимно-однозначное соответствие. Дублирующей программой называется программа Р, такая, что для некоторых Уь Угс: У при заданном расположении ЦМД Xi с: Vi программа Р образует копию Xi в Уг без изменения Xi в Уь

Теорема 8.2 [И]. Не существует дублирующей программы Р = eiCz, е-п.

Рис. 8.11. Четыре типа операций ЦМД.

ЭТО взаимодействие позволяет реализовать разветвление при передаче переменной а. Для обеспечения запуска мы добавим еще один тип взаимодействия - образование ЦМД, обозначаемое как е = {1,А), при этом

Х'-Х[]{А},

а также разрушение ЦМД, обозначаемое как е= (О, Л), для которого

Х' = Х-{А}.

Характеристики всех четырех типов взаимодействия сведены вместе в таблицу, представленную на рис. 8.11.

Даже если мы сможем воспользоваться всеми рассмотренны-типами взаимодействий, все комбинационные функции нельзя

Следствием теоремы 8.2 является невозможность реализации разветвления по выходу на основе только передачи ЦМД. Следовательно, нельзя реализовать все комбинационные функции, используя только эти команды, хотя И, ИЛИ и НЕ могут быть реализованы при использовании показанного на рис. 8.9 метода кодирования [13]. Однако можно реализовать и другие типы команд, которые можно ввести в нашу модель, не сделав ее при этом нереалистичной. Для реализации разветвлений мы рассмотрим другой тип взаимодействия, названный расщеплением ЦМД, и обозначим его е - {А, B)s, при этом

X = X[j{B), если А^Х, В^Х,

Х^ = Х, если АфХ или В^Х.

После этого взаимодействия ячейки А и В представляют а'=а, Ь' = а-\- Ь. Если первоначально в ячейке В не было ЦМД, то

реализовать без использования ячеек для временного хранения ЦМД.

Теорема 8.3 [10]. Четырех типов команд (передачи, расщепления, уничтожения и создания ЦМД) не достаточно для выполнения всех вычислений, если все ячейки множества V содержат информацию.

Доказательство. Рассмотрим программу Р, образующую дополнение к содержимому каждой ячейки V, т. е. = V-X. Пусть Ci - первая команда программы. Докажем, что не существует программы Р вычисления V - X, которая использует только четыре типа названных команд, показав, что для каждого типа команд существуют два множества Xi Ф Хг, таких, что XV = XV- Следовательно, поскольку V - Х^Ф V - Хг, программа не может вычислять V - X для всех X.

Случай 1. Пусть ei = (Л, В).

Положим Хг= {Xi - {A)){j{B}; ЛеХ,; В ф Xi. Тогда Xl - Хг = Хг и Х^ ---- Хг.

Случай 2. Пусть d = {А, В),. Пусть Л е В е X а Хг = = Xl и {В}. Тогда

Xf = Xf = Хг и Xl = Хг.

Случай 3. Пусть е1=(0,Л). Положим ЛеХь а Х2 = = Xi -{Л}. Тогда

Xf = xf = Хг и Xl = Хг-

Случай 4. Пусть ei = (1, Л).

Положим Л е Хь а Хг = Х| - {.Л}. Тогда

Xl = Хг == Xl и xf = Хг.

Следовательно, не существует программы Р, использующей только четыре типа команд, которая способна вычислять V - X для всех X.

Теорема 8.3 подразумевает, что если даже V содержит 2п разрядов, которые представляют значения п переменных на основе использования кодирования, показанного на рис. 8.9, то все равно не существует программы, обеспечивающей получение дополнений для всех переменных сразу. Вспомним теперь, что для обсуждавшейся ранее программы дополнения двоичной переменной требовалось наличие дополнительной ячейки.

Теорема 8.4 [10]. При наличии достаточного числа ячеек для временного хранения на основе использования четырех типов команд и соответствующего кодирования входных переменньгх можно вычислять все комбинационные функции,

Доказательство. Любая комбинационная функция f{Xi,x2,..-..., Хп) может быть реализована на основе следующего метода. Пусть V = S\jT и S []Т = ф, где V - множество всех ячеек, S - множество, используемое для представления входов и выходов, а Т = {А, В} - множество (двух) ячеек, используемых для промежуточного хранения. Пусть также каждая входная переменная Х{ будет представлена двумя ячейками Хго, Хц е S, а ячейки Fo, Fi е S будут представлять выходную функцию. Комбинационная функция f и ее дополнение f выражаются сначала в виде суммы произведений, что достигается при помощи следующей процедуры.

1. Очистить выходные ячейки командами (О,Fo) (О, Fi).

2. Вызвать ячейку А с помощью команды (1, Л).

3. Для каждого литерала х*, содержащегося в терме Р, использовать последовательность команд (О, В), {Xij, В), {А, В) для формирования частичных произведений Р в ячейке А. Здесь х] обозначает х. или ж., а q = 0, если х*. = х. и <?==!, если х*. = х..

4. По окончании формирования каждого терма присоединить его через элемент ИЛИ к уже полученным термам при помощи {A,Fi).

5. Если еще есть другие термы, возвратиться к шагу 2 и повторить указанные действия для следующего терма.

6. Если термов больше не осталось, повторить шаги 2-5 для f, заменяя команду на шаге 4 командой (Л, Fq).

В процедуре теоремы 8.4 не делалось попытки минимизировать число команд, необходимых для реализации функции. Задачи эффективной реализации мы рассмотрим в следующем разделе.

В разд. 8.2 мы видели, как для двух переменных можно реализовать операции Исключающее ИЛИ и И на основе использования взаимодействия магнитных доменов. Для таких взаимодействий можно также построить математическую модель [10]. Поскольку И и Исключающее ИЛИ составляют слабо полное множество простейших логических элементов (как показано в гл. 2), то на основе использования перечисленных взаимодействий может быть реализована любая комбинационная функция, если имеется единичная константа (т.е. источник ЦМД) и возможна реализация разветвлений. Разветвление можно реализовать на основе этих же взаимодействий, поскольку взаимодействие между ячейкой, содержащей единичную константу, и ячейкой, представляющей переменную х, дает х или х. Процедуру можно повторять для получения нужного числа копий х. Более того, при этом не требуется специального кодирования, поскольку осуществима операция взятия дополнения.,

8.4. ЗАДАЧИ ОПТИМИЗАЦИИ

Мы рассмотрели математическую модель взаимодействия магнитных доменов и выяснили, как на их основе можно реализовать все логические функции. Однако процедура, описанная в теореме 8.4, может оказаться очень неэффективной. Теперь мы рассмотрим некоторые специальные задачи, связанные с эффективной реализацией логических функций на основе взаимодействия магнитных доменов. Логические элементы, разработанные на основе использования магнитных доменов, обладают следующими особенностями:

1. Заставить взаимодействовать между собой можно только соседние ЦМД. Следовательно, для выполнения последовательности взаимодействий необходимо учитывать ограничения на схему расположения ячеек памяти и вообще необходимо предусмотреть транзитные точки для передачи ЦМД, не являющихся соседними, в смежные позиции без повреждения других ЦМД. Это приводит к необходимости увеличения необходимого числа ячеек.

2. Необходимость согласования во времени. ЦМД продвигаются на фиксированное расстояние за каждый оборот поля или при прохождении каждого импульса тока. При реализации многовходовых логических операций протяженности входных путей должны быть согласованы таким образом, чтобы входные данные прибывали во взаимодействующие ячейки в соответствующие моменты времени.

3. Отсутствие логического эквивалента провода. Информация, представляемая ЦМД, находящимися в определенных ячейках, передается в другие ячейки, где она может понадобиться, при помощи последовательных пересылок ЦМД между смежными ячейками.

4. Разветвление по входу и выходу, а также пересечения требуют взаимодействия магнитных доменов и должны реализовываться за счет увеличения сложности логики.

5. ЦМД должны создаваться и разрушаться.

Эти особенности логики, разработанной на основе ЦМД, существенно усложняют рассматриваемые далее задачи оптимизации.

8.4.1. СОГЛАСОВАНИЕ ВО ВРЕМЕНИ И ПРОСТРАНСТВЕ

Поскольку взаимодействие возможно только между ЦМД, находящимися в физически смежных ячейках, то подразумевается, что ЦМД, взаимодействие которых необходимо, должны быть перемещены в смежные ячейки до того, как начнет исполняться команда. Время, необходимое для вычисления функции.

зависит не только от числа команд программы, но также и от расположения используемых программой ячеек. Может также потребоваться перемещение ЦМД между двумя несмежными ячейками без повреждения его в других ячейках.

Каждая ячейка, которая содержит ЦМД, составляет, по существу, бит памяти. Мы будем называть схему расположения ячеек ЦМД схемой памяти. Те ячейки ЦМД, которые содержат информацию, такую, как значения входных переменных, промежуточные результаты и т.д., мы будем называть ячейками данных. Для перемещения ЦМД между несмежными ячейками могут потребоваться дополнительные ячейки, называемые транзитными ячейками.

Рассмотрим сначала схемы памяти, которые могут быть использованы для любой программы, для которой требуется п ячеек данных. Для этих схем необходимо, чтобы выполнялось следующее требование: ЦМД, находящиеся в любой паре ячеек, можно переместить в смежные ячейки без повреждения ЦМД в других ячейках. Вообще большинство программ не требуют взаимодействия всех пар ячеек. Схемы памяти для отдельных программ могут потребовать меньше транзитных ячеек, чем предусмотрено в общем случае. Схемы расположения, обеспечивающие все возможные взаимодействия, называемые универсальными структурами памяти, могут использоваться любой программой и, следовательно, могут служить для оценки сложности схем в наихудшем случае.

8.4.2. УНИВЕРСАЛЬНЫЕ СТРУКТУРЫ ПАМЯТИ

Рассмотрим схему расположения, изображенную на рис. 8.12. Если ячейки, находящиеся в заштрихованной области, используются в качестве ячеек для хранения данных программы, то ячейки, находящиеся в незаштрихованной области, используются в качестве транзитных ячеек. Эти транзитные ячейки при инициализации не содержат ЦМД. Обозначая заштрихованные и незаштрихованные области соответственно через МиГ, заменяем команду типа (А, В), где А,В^М, последовательностью команд:

(А, Xi){Ki, Xi,), (Z; b B){Xj, ...

Xd{Xi, A),

где Xi и Zj смежны соответственно с Л и В, a X Xi+x Xj-i, XjT-последовательность смежных точек. Заметим, что последовательность состоит из двух частей, одна соответствует пути из ячейки Л в В, а другая из ячейки В в Л. Это необходимо для того, чтобы перенести результаты взаимодействия обратно

Рис. 8.12. Универсальная структура памяти

любой универсальной структуры памяти асимптотически стремится к 2р/3. Следовательно, схема расположения, показанная ка рис. 8.12, асимптотически оптимальна и обеспечивает максимальное чрсло ячеек данных при заданном общем числе ячеек.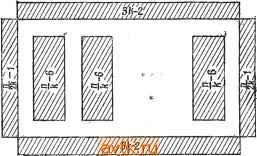

Рис. 8.13. Универсальная структура памяти с уменьшенной максимальной

длиной пути.

Время, необходимое для взаимодействия двух ячеек Л и fi, зависит от длины пути между Л и fi, проходящего через транзитные точки. Максимальная длина пути между двумя точками (в предположении, что расстояние между соседними ячейками равно 1) равна п/2. Максимальную длину пути можно значительно уменьшить за счет некоторого увеличения используемой памяти (т. е. общего числа ячеек) на основе использования схемы размещения, показанной на рис. 8.13. Общее число ее ячеек равно (П/2Й - 1) ЗА -f- 6 - 4 = 3n/2 -f ЗА - 4, а общее число ячеек данных равно 6A - 4-\- {k - 1) {n/k - 6)-- 2(n/2A - 1) =n.

Максимальная длина пути равна п/2й-+-ЗА -3. Максимальная длина пути зависит от k. Поскольку k должно быть целым.

В ячейки Л И fi. То же взаимодействие могло бы основываться на перемещении ЦМД из ячеек Л и fi в пару смежных ячеек того же пути и последующего возвращения результата обратно в ячейки Л и fi.

Для схемы памяти, изображенной на рис. 8.12, для п ячеек данных необходимо Зп/2- 1 ячеек. Если р - общее число ячеек, то можно показать, что максимальное число ячёбк данных Для