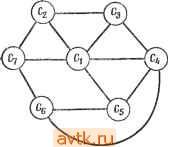Рис. 7.54. К упражнению 7.20.

б) Граф, показанный на рис. 7.54, является графом пересечений для множества из 7 соединений Cj, Сг, .... С?. Сколько слоев должна иметь плата для того, чтобы была возможна трассировка без образования пересечений?

в) Если требуется k слоев, а используется только {k-1)-й слой, то каково минимальное число пересечений?

7.21. а) Схему, изображенную на рис. 7.55, требуется разбить на три блока, содержащих не более трех элементов каждый. Один блок должен содержать элементы (1, 2, 3), другой блок - элементы (4, 5, 7). Оставшиеся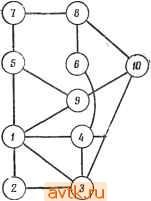

Рис. 7.55. К упражнению 7.21.

элементы надо разбить на два блока, используя процедуру Кернихана - Лина (процедура 7.1). Предположим, что существует версия алгоритма Кернихана- Лина, которая применима к графам и входными данными которой является матрица С соединений между парами элементов. Пусть при помощи этого алгоритма множество элементов разбито на два блока на основе

минимальное число цветов, необходимое для раскраски всех вершин графа G таким образом, чтобы не было пи одной дуги, соединяющей две вершины одного цвета. Покажите, что k и есть хроматическое число графа пересечений, определяемого Си Сг, ..., Ср.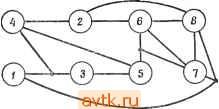

Схема

Разметка позиций Исходнов размещвше

Рис. 7.56. К упражнению 7.22

Рис. 7.57. К упражнению 7.23.

случайно выбранного исходного разбиения. Постройте, если это возможно, матрицу С и промоделируйте работу программы при решении этой задачи, если требуется минимизировать общее число соединений между тремя блоками.

б) Разбейте схему на два блока, содержащих каждый от 4 до 6 элементов, используя исходное разбиение (1234, 5678910).

7.22. Для схемы, показанной на рис. 7.56, требуется улучшить исходное размещение, используя процедуру 7.П. Используйте минимальное несвязное множество с наибольшим числом элементов.

7.23. Пусть на изображенной на рис. 7.57 сетке требуется провести два соединения {А, А') и {В, В'), используя алгоритм Ли для случая прямоугольного расстояния. Функция упорядочения g является комбинацией нескольких предложенных упорядочений

g(C, C) = L(C, C) + D{C, С),

где L{C,C)-длина кратчайшего прямоугольного пути между С и С, D{.C,C)=2n{R(C, C))-\-hX (Незанятая площадь внутри R(C, С'))/Общая площадь R{C,C); здесь fei -некоторая постоянная величипа. Минимизируемая оптимизационная функция f = L - 2Vp + 3.<-Ь 2Vy, где L - длина пути, Ур - число клеток пути, которые граничат с хотя бы одной из исполь зованных ранее клеток, Vf - число клеток пути, граничащих с клетками, требуемыми для последующих соединений, К - число пересечений. (Заметим, что пересечения не запрещены. Следовательно, ранее использованные клетки могут быть частью оптимального пути. Число пересечении К определяется как число ранее использованных клеток данного пути.)

а) При каких значениях fe, О первым реализуется соединение (Л, А') ? (Первым реализуется соединение с наименьшим значением функции g.)

б) При каких значениях fe, О первым реализуется соединение (В, В') ?

в) Для fei = 40 укажите в соответствии с методом Ли оптимальный вариант трассировки. Если таких вариантов несколько, укажите все.

Глава 8 МАТЕМАТИЧЕСКИЕ МОДЕЛИ ЛОГИКИ НА ЦИЛИНДРИЧЕСКИХ МАГНИТНЫХ ДОМЕНАХ

8.1. ВВЕДЕНИЕ

В изложенных в предшествующих главах технологиях в большинстве задач рассматривалась минимизация числа компонент схемы- Для проблем, связанных с использованием современной технологии, все более важными становятся вопросы структуры и модульности. Бесспорно, что технологии будущего изменят этот круг вопросов. При рассмотрении любой новой технологии общий подход состоит в построении модели, отражающей физические особенности технологии и позволяющей формулировать наиболее существенные задачи проектирования в удобной математической форме. При этом многие задачи, возникающие на основе рассмотрения новой модели, сходны с задачами, связанными с использованием старых технологий.

В этой главе будут рассмотрены такие модели для задач физического проектирования, связанные с технологией, основанной на использовании цилиндрических магнитных доменов, которая представляется перспективной для будущих цифровых систем. Как будет ясно из дальнейшего, при моделировании логики на цилиндрических магнитных доменах оказывается возможным учитывать требования модульности проектируемых систем. Возникающие при этом задачи определения временных соотношений сходны, хотя и не идентичны, такого рода задачам, возникающим при проектировании асинхронной логики. Наряду с этим при проектировании логики на магнитных доменах возникают и принципиально новые задачи, связанные с рассмотрением других классов функций.

Как представляется в настоящее время, по-врщимому, магнитные домены будут использоваться в будущем в цифровых системах, в которых потребуется большой объем памяти наряду с малой потребляемой мощностью. При использовании таких устройств возникнет потребность в минимизации числа дорогостоящих стыков с устройствами, разработанными на основе других технологий. В силу этого практический интерес представляет разработка развитой логики на магнитных доменах.

Несмотря на то что магнитные домены можно рюпользовать для выполнения логических операций, получаемая скорость функционирования на несколько порядков ниже скорости, достигаемой при использовании современной полупроводниковой технологии. Этот фактор накладывает ограничения на использование магнитных доменов. Однако очень низкая по-

8.2. ФИЗИЧЕСКИЕ ОСНОВЫ

Внешнее тле смещения

Определенные типы магнитных материалов, например монокристаллы магнитных окислов и ортоферритов, обладают тем свойством, что их проще намагнитить в одном определенном направлении, чем в других. В тонкой пластине такого материала, направление простого намагничивания которого перпендикулярно поверхности пластины, при определенных условиях могут быть созданы стабильные магнитные домены. Направление намагничивания таких доменов противоположно направлению простого намагничивания. При наложении внещнего поля эти магнитные домены могут быть цилиндрическими. Такие цилиндрические магнитные домены называют сокращенно ЦМД. На рис. 8.1 показан поперечный разрез ортоферритовой пластины и указаны направление внешнего поля и направление поляризации ЦМД. В зависимости от типа используемого материала размеры ЦМД могут изменяться от единиц до нескольких сотен микрон.

Размеры и форма магнитных доменов определяются силой и направлением внешнего поля.

При ослаблении магнитного поля диаметр магнитных доменов увеличивается и они теряют цилиндрическую форму. Увеличение наклона магнитного поля приводит к уменьшению размера ЦМД и их дальнейшему разрушению.

Расположение ЦМД в пластине может быть ограничено конечным множеством возможных позиций. Наличие или отсутствие ЦМД в конкретной ячейке может логически интерпретироваться как наличие соответственно двоичных 1 или 0. ЦМД можно перемещать из одной позиции в другую, рассматривая их как заряженные частицы. ЦМД отталкиваются друг от друга, и это их взаимодействие может быть использовано для построения логических элементов. Таким образом, представляется возможность применения магнитных доменов для обработки данных.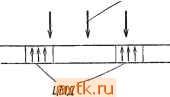

Рис. 8.1. Ортоферритовая пластина, ЦМД и поле в поперечном разрезе.

требляемая мощность делает заманчивым их использование в тех случаях, когда высокая скорость функционирования не требуется.

8.2.1. ПЕРЕМЕЩЕНИЕ ЦМД

Для перемещения ЦМД по пластине применяются различные методы. На рис. 8.2 иллюстрируется метод, основанный на образовании локальных магнитных полей при помощи электропроводящих петель. Петли напыляются на содержащую ЦМД орто-ферритовую пластину. Электропроводящие петли делаются полузамкнутыми, как показано на рис. 8.2, для облегчения использования тонкопленочной технологии. ЦМД могут быть перемещены из-под одной петли к соседней, через которую для этого пропускается импульс тока в направлении, обеспечивающем ослабление внешнего поля. На рис. 8.2 импульс тока, проходящий через петлю Xs, обеспечит перемещение ЦМД из t, ъ Н.ъ то время как такой же импульс, пропущенный через петлю Xl, переместит ЦМД из £ в S. Таким образом, можно переместить ЦМД в любую соседнюю петлю. Однако возникает необходимость наложения компенсирующих магнитных полей путем пропускания импульсов тока через соответствующие петли, для того чтобы удержать на месте ЦМД, которые не должны перемещаться.

Если на материал напыляется еще один набор петель, перпендикулярных наложенным ранее (рис. 8.3), то ЦМД из любой позиции может быть перемещен в любую из четырех соседних позиций. Следовательно, ЦМД можно переместить в любую позицию путем подачи последовательности импульсов тока. Изображенный на рис. 8.3 ЦМД можно переместить из позиции А в позицию Н, подавая последовательность импульсов Уг, Уз, Х^ или Хг, Уг, Уз или Уг, Хг, Уз-

Другой метод перемещения ЦМД основан на использовании пермаллоевого надслоя и вращающегося магнитного поля [6]. Пермаллой наносится на пластину, содержащую ЦМД. На рис. 8.4 показана широко использующаяся структура магнитного материала, состоящая из линейных и Т-образных элементов. Перемещение пузырьков в таких структурах называется Т-ли-нейной передачей.

При Т-линейной передаче ЦМД для обеспечения их устойчивости необходимо смещающее поле. Для перемещения ЦМД используется другое поле, вращающееся в плоскости материала. Вследствие высокой магнитной проницаемости пермаллоевой пленки плоское магнитное поле порождает магнитные домены в пермаллоевом надслое. При любом направлении плоского маг-

R R О

W й \\

л, л2 Лз

Рис. 8.2. Перемещение ЦМД при помощи проводящих петель.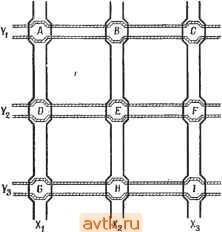

U Ега

1±1 q=p

Рис. 8.3. Перемещение ЦМД по пло- Рис. 8.4. Т-линейная передача, скости при помощи проводящих петель.

Перемещение ЦМД в пермаллоевом надслое, используемое, в частности, в рассмотренном метод Т-линейной передачи, широко используется на практике вследствие возможности простого управления процессом перемещения. При использовании проводящих контуров для перемещения ЦМД из одной позиции в другую импульсы тока должны пропускаться через петли в определенной последовательности. При Т-линейной передаче это требование отпадает. Регистр сдвига, например, можно реализовать на основе Т-линейной передачи так, как показано на рис. 8.4. ЦМД будет продвигаться от одного Т-элемента до следующего за каждый цикл вращения магнитного поля.

8.2.2. ОБРАЗОВАНИЕ, РАЗРУШЕНИЕ И ОБНАРУЖЕНИЕ ЦМД

Пермаллоевые схемы используются также для образования и разрушения ЦМД [5]. Образование ЦМД завершается разделением его на две части, как показано на рис. 8.5. Большой

НИТНОГО ПОЛЯ ЦМД достигают энергетически выгодной позиции.

Перемещение ЦМД, вызванное вращением плоского магнитного поля, можно рассматривать как перемещение магнитных зарядов , которые отыскивают положительные полюса пермаллое-вого магнита. На рис. 8.4 иллюстрируется движение одного ЦМД за один оборот вращающегося поля. При изменении направления вращения на противоположное перемещение ЦМД происходит в обратном порядке.

пермаллоевый диск на входе пути Т-линейной передачи содержит исходный ЦМД. Вращение магнитного поля обусловливает за-? хват ЦМД Т-элементом, вытягивание и, наконец, разбивку ЦМД

на две части в соответствии с рис.8.5. Оба образовавщихся ЦМД приобретают затем размеры, определяющиеся внещним полем. Один из ЦМД остается на пермаллоевом диске, другой продвигается по пути из линейных и Т-образных элементов. ЦМД могут быть разрушены путем слияния их в один ЦМД - сток , находящийся в конце Т-линейного пути. Как указывалось выше, ЦМД можно также разрушить под действием сильного внешнего поля.

При стыковке памяти на магнитных доменах с традиционными схе- R сёл R мами должна существовать возмож-4++ ность определения наличия ЦМД в определенных позициях и генерации Рис. .5. Образование ЦМД соответствующих электрических сигналов. К методам обнаружения магнитных доменов относятся метод магнитооптического обнаружения, обнаружение на основе использования эффекта Холла и обнаружение при помощи магниторезистивных устройств [1].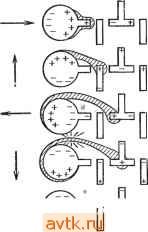

8.2.3. ЛОГИЧЕСКИЕ ОПЕРАЦИИ

Далее будет рассмотрена реализация некоторых логических функций на основе использования магнитных доменов. При реализации используется тот факт, что ЦМД, находящиеся в смежных позициях (ячейках), отталкиваются друг от друга. ЦМД можно перемещать в нужные позиции на основе любой из двух вышеописанных схем перемещения. В обеих схемах ЦМД перемещаются на фиксированное расстояние при прохождении каждого импульса тока или при каждом обороте поля. Следовательно, неотъемлемым свойством логических устройств, использующих магнитные домепы, является синхронность функционирования.

На рис. 8.6 иллюстрируется метод реализации некоторых простых логических функций двух переменных на основе использования проводящих петель. ЦМД, представляющие переменные Xl и Хз, передвигаются сначала в ячейки А и В. Это значит, что позиция А содержит ЦМД тогда и только тогда, когда Xi = I, а позиция В содержит ЦМД тогда и только тогда, когда Хз = 1,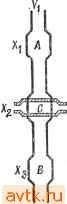

Предположим, что первоначально в ячейке С не содержится ЦМД. Если теперь через Хг пропустить импульс тока, то ЦМД. находящиеся в ячейках А и В, будут стремиться перейти в ячейку С. Однако если в обеих ячейках А я В содержатся ЦМД, то они будут отталкиваться друг от друга. Следовательно, после прохождения импульса тока через Хг ячейка С содержит ЦМД тогда и только тогда, когда до прохождения импульса лиГ^ь одна из ячеек А или В, но не обе одновременно содержала ЦМД. Поскольку ячейка А первоначально представляла переменную Хи а ячейка В - переменную х^, то ячейка С будет представлять логическую функцию Х\ ф лгд. Ячейки А я в будут содержать ЦМД в том и только том случае, если обе они первоначально содержали ЦМД. Таким образом, ячейка А, так же как и ячейка В, представляет функцию Xi-Xg.

Если расположение позиций не симметрично, то даже в том случае, когда обе ячейки А я В содержат ЦМД, можно гарантировать перемещение ЦМД в ячейку С в ответ на импульс тока, переданный через Хг. Ячейка С теперь представляет функцию Xl + Хз. Такая же конфигурация может быть использована для получения в ячейке С функции Xi-Xz. Действительно, пропустим импульс тока через Хг\ в том случае, когда ячейки А и/или В содержат ЦМД, это приведет к появлению ЦМД в ячейке С. Далее, пропустим импульс тока с соответствующей амплитудой через Хг, но уже в обратном направлении. Это усилит внешнее поле, которое разрушит ЦМД, находящийся в ячейке С (если таковой имеется). И наконец пропустим через Xz еще один импульс, который передвинет в ячейку С ЦМД, еще оставшийся в ячейке А или В. После прохождепря этих трех импульсов тока ячейка С будет содержать ЦМД в том и только том случае, если ЦМД первоначально присутствовали в обеих ячейках А я В.

Для реализации логических функций может также использоваться и Т-линейная передача, как иллюстрируется на рис. 8.7. При вращении плоского поля в направлении, показанном стрелкой на рис. 8.7, ЦМД, находящиеся в ячейке А (представляюще переменную Xi) и/или в ячейке В (представляющие переменную Хг), перемещаются по направлению к ячейке С. Из этой точ1<и ЦМД могут продолжить движение по направлению к ячейке Х> или Е. На основе специального размещения линейных и Т-образных элементов в месте пересечения двух путей и при условии

Рис. 8.6. Реализация логических функций на основе исполь:!ОвайИя проводящих петел*>.

отсутствия других ЦМД в данной окрестности оказывается возможным направить ЦМД по одному конкретному пути, который называется простым путем. Эффект отталкивания от соседних ЦМД может привести к тому, что ЦМД начнет перемещаться в другом направлении, называемом трудным путем.

Вращающееся J пот

Рис. 8.7. Реализачия логических функций на основе использования Т-линей-♦ ной передачи ЦМД.

Пусть на рис. 8.7 направление к ячейке D будет простым путем из ячеек Л и В.

Если первоначально ЦМД находится в одной из ячеек Л или В, то он будет передвигаться по легкому пути. Если и в ячейке

Вращающееся поле

ееся у

-3,....

Рис. 8.8. Т-линейная реализация пересечения проводников.

Л и ячейке В содержатся ЦМД, то они прибудут в ячейку С в одно и то же время. Один из ЦМД при этом будет вытолкнут на трудный путь в сторону ячейки Е, в то время как другой будет продвигаться по легкому пути в сторону ячейки D. Следовательно, ячейка D представляет функцию Xi-\-x2. При определенной геометрической структуре пермаллоевого надслоя аналогичным образом можно реализовать и другие основные логические функции.