ИЗ с,- в Cj, проходящий через Сй, обозначается как p(ci, Cj, Ck).

В общем случае требуется найти путь, оптимальный относительно некоторой функции качества F (или множества {Fl F2.....Fr) таких функций).

Путь р1 (с,-, Cj) называется минимальным по отношению к некоторой функции качества F, если F{pi{ci, Cj)) F {pk{ciCj)) для всех pkici, Cj) GTC*{Ci, Cj). Функция качества F является монотонной, если F{px{Ci, Cj)) F (pi(ci, Cj, c)), где Pi(Ci, с,-) является частью пути pi(cj, Су, Ck).

Алгоритм Ли может быть использован для построения пути между двумя ячейками, который является минимальным по отношению к некоторой функции F, при условии, что F является монотонной и F{p(Ci, Cg, Cj)) = F(pi{Ci, Cg)) + F(p2{cg, Cj)), где

P (Ci, Cg, Cj) = Pl (Ci, Cg)p2 (Cg, Cj).

Следующая процедура обеспечивает построение кратчайшего пути из Ci в Cj, который минимизирует функцию F, в случае если F удовлетворяет указанным ограничениям.

Процедура 7.16

1. Строим дерево с исходной вершиной й и ветвями, идущими от Ci к Ст для всех допустимых клеток CmN(Ci). Сопоставляем с каждой вершиной цену F(Ст) = F(р{d, Ст)), где p(Ci,Cj) - путь единичной длины от Cj к с^.

2. Строим следующий уровень дерева следующим образом: для каждой имеющей минимальную цену вершины с^, являющейся конечной вершиной некоторой ветви, образуем ветвь, идущую от этой вершины к каждой из допустимых клеток с^еЛ(с^), а соответствующую цену определяем как f =

(m + CPCmт))- Р* возможна ситуация, когда идущая к вершине ветвь уже была образована раньше (т. е. существует другой путь, содержащий с^). В этом случае мы обрываем ветвь, которая имеет большую цену.

3. Если с' = с. и F (с^) < F (с^), где через обозначена любая конечная вершина некоторой ветви, то путь из с,-в c = Cf является оптимальным путем из с. в е.. В противном случае шаг 2 повторяется до тех пор, пока не будет образован оптимальный путь к С/ или не будет показано отсутствие такого допустимого пути.

Процедура 7.16 может быть использована для оптимизации относительно нескольких функций Fi, F2, F . Соответствующие некоторому пути значения F располагаются в порядке убывания важности соответствующих целей. Оптимальным является путь, обеспечивающий минимум Fi. Если такой путь не один, то

Путь 3

-Путь г

Путь 1

для определения оптимального пути используются попорядку

Теперь мы продемонстрируем возможность определения монотонной оптимизационной функции для построения последовательных соединений. Рассмотрим рис. 7.47. Предположим, что элементы В н В' должны быть соединены и к ним надо присо-.единить элемент С. На приведенном рисунке указаны три возможных пути соединений. Путь 1 использует две из смежных

с С клеток и, следовательно, как бы изолирует С. Путь 2 - это путь, не проходящий через клетки, смежные с запрещенными, и, следовательно, он как бы стремится разделить сетку, но ближе к проложенному соединению. Пусть 3 не использует клеток, смежных с С, и является смежным для уже проложенного соединения. Поэтому, хотя этот путь имеет большую протяженность, чем первый и второй пути, он с меньшей вероятностью помешает проведению последующего соединения к С. Во избежание возможных изоляции и разбиения плоскости в процедуре 7.16 может быть использована следующая эвристически выбранная оптимизационная функция:

F = (L-Vp) + kVp,

где L - длина пути, Vp - число клеток, смежных по отношению к пути, для которого потребуются последующие соединения (при этом если клетка смежна нескольким клеткам пути, она будет учитываться несколько раз), Vp - число клеток пути, которые являются смежными для предыдущих соединений, а /е - константа, выбираемая в соответствии с относительной важностью всех трех, учитываемых в F факторов. При k - 2 значения F для путей, изображенных на рис. 7.47, равны F(Pi)= 10, р(Р2)=8, Р(Рз) = 4. Можно считать, что сетка имеет размер (п--2)Х ( + 2), но ее граничные клетки не используются (их можно рассматривать как уже проложенные соединения), т.е. рассматривается сетка пу п.

При использовании специальных технологий наличие пересечений оказывается допустимым, хотя и дорогостоящим. Процедуру 7.16 можно использовать и в этом случае, назначая до-

Рис. 7.47. Трассировка при использовании сложной оптимизационной функции

полнительную цену для клеток, которые уже были ключены в некоторый путь. Тем не менее необходимо проверить, что эти пути, пересекаясь, не перекрываются.

На практике трассировка производится и на многослойных платах. Выводы уже размещенных элементов могут проходить через все слои, на каждом из которых могут быть реализованы соединения. При этом чем больше число слоев, тем больше число соединений, которые можно провести, не образуя пересечений. Помимо этого некоторые клетки платы могут содер>}<ать отверстия ( путепроводы ), для соединения различных с^юев. Путепроводы можно использовать для передачи по нескользким слоям сигналов, трассировку которых нельзя произвести в одном слое платы. Размещение путепроводов на печатной плате цдожет быть

Рис. 7.48. Многослойная плата.

ограничено определенными областями ( фиксировашгыми путепроводами ), при этом на использование путепровСДа назначается определенная цена. Процедура 7.16 может бы-гь модифицирована для трассировки многослойных плат. Соедм^ение между л и л' прокладывается из k (где а -число слоев) исходных вершин к k конечным вершинам. Клетки, которые мсргут содержать путепровод, отмечаются специальным символом, и множество клеток, соседних с отмеченными, включает соответствующие клетки других уровней. Для обоснованного использования путепроводов мы можем воспользоваться оптимизационной функцией F -~ k-V + L, где У -число использованных путепроводов, L - длина пути, а -некоторая постоянная (которая выбйрается таким образом, чтобы достигалось правильное соотношение между выгодой от использования путепровода и теми сложнС)СТЯми, которые с этим сопряжены, например осложнением про*<ладки последующих соединений). Использование путепроводов может упростить и соединение между двумя точками ле?кащими в одном и том же слое.

Рассмотрим случай двухслойной платы (рис 7 48). Пусть требуется соединить между собой точки а и Ь, принадлежащие слою 1. Клетки, через которые могут быть проложен!?! путепроводы, отмечены символом О, и часть соединений уже 1Проложена в соответствии с рис. 7.48. Проложить требуемое соединение,

Слой 1 а

Слой г

Рис. 7.49. Трассировка с использованием сквозных переходов ( путепроводов ).

перпендикулярных отрезков), можно сформулировать как задачу о раскраске графа (задача 7.20). Общепринятым решением при двухслойной трассировке является размещение всех горизонтальных отрезков в одном слое, а всех вертикальных - в другом.

В числе других используемых процедур можно назвать алгоритм Ли. Большинство других методов, хотя и являются более быстрыми, могут не дать решения, даже если оно существует. Один из таких методов основан на образовании путей не в виде последовательности клеток, а в виде последовательностей отрезков [16]. В другом методе, названном трассировкой каналов, сначала прокладываются соединения между строками и/или столбцами, состоящими из каналов. Каждый канал может содержать не более определенного числа соединений. После распределения между каналами производится трассировка соединений по трактам каналов.

Для того чтобы алгоритм трассировки был эффективен, он должен обеспечивать ослабление взаимного влияния прокладываемых соединений. Было показано, как можно повысить эффективность однопутевой трассировки на основе использования эвристических процедур, обеспечивающих предотвращение изоляции отдельных вершин или разделения платы. В числе других методов, увеличивающих эффективность трассировки, можно назвать параллельную трассировку, при которой вместо определения одного пути одновременно определяются несколько путей.

используя только СЛОЙ 1, невозможно. Однако это возможно при использовании двухслойной платы; на рис. 7.49 пунктиром показано соединение, длина которого равна 8, при этом используются два путепровода. Слой 2 в этом случае использовался только для того, чтобы избежать пересечений в слое 1.

При использовании нескольких уровней возникает дополнительная задача определения слоя (или слоев) для прокладки каждого соединения. Акерзом [3] показано, что задачу определения числа слоев, необходимых для трассировки соединений в евклидовом пространстве (где две точки соединяются единственным отрезком напрямик, а не ломаной из двух взаимно

а также адаптивные процедуры, допускающие изменение уже построенных путей для прокладки последующих соединений. Несмотря на то что указанные методы исследовались, в настоящее время не существует удовлетворительных методов отыскания решений при допустимых вычислительных затратах.

БИБЛИОГРАФИЯ И КОММЕНТАРИИ

Сведения общего характера по физическому проектированию можно найти в обзоре Брёйера {6] и в книге под его редакцией [5]. Сведение задачи разбиения схемы к задаче о покрытии содержится в работе Лаулера [20]. Эвристическую итеративную процедуру предложили Кернихан и Лин [18]. На преимущества дублирования указали Руссо, Оден и Вульф [30]. Математический подход к решению задачи о разбиении был разработан Лючио и Сами [25]. Разбиение при минимизации длительности задержки рассмотрено в работе Лаулера и др. [21], разбиение на единообразные модули рассматривалось Стоуном [33].

Граничные оценки для задачи о размещении получены Гил-мором [11]. Гэрсайд и Никольсон [8], Лоберман и Вейнбергер [23], Стейнберг [32] и Рутман [31] предложили различные методы размещения, обзор которых представили Хэнон и Куртзберг [14]. Алгоритм нахождения оптимальной перестановки принадлежит Манкресу [28]. Минимальные деревья покрытий исследовали Крускаль [19] и Прим [29], а деревья Штейнера - Гилберт и Поллак [10] и Хэнон [12, 3]. Ахо, Герей и Хуанг [2] рассматривают эту задачу для специальных случаев, когда все вершины лежат на небольшом числе параллельных прямых или на границе прямоугольника. Задача определения порядка реализации соединений рассматривалась Абелем [1]. Основная процедура трассировки принадлежит Ли [22] и основывается на использовании алгоритма обхода лабиринта, предложенного Муром 27]. Другие процедуры разработали Хичкок [17], Хайтауэр [16] Фиск и др. [7], Гейер [9] и Акерз [3]. Эвристические методы выбора и размещения интегральных схем и назначения карт были предложены Хаспелем [15].

ЛИТЕРАТУРА

1. Abel L. С, On the Ordering of Connections for Automatic Wire Routing, IEEE Trans, on Computers, vol. C-21, pp. 1227-1233, November 1972.

2. Aho A. v., Garey M. R., Hwang F. K., Rectilinear Steiner Trees: Efficient Special-Case Algorithms, International Memorandum, Bell Telephone La boratories, 1974.

3. Akers S. В., Some Problems and Techniques of Automatic Wire Layout. Digest of First Annual 1ЕЁЕ Computer Conference, September 1967.

4. Alia G., Frosini G., Maestrini P., Automated Module Placement and Wire Routing According to a Structured Biplanar Scheme in Printed Boards, Computer Aided Design, vol. 5, pp. 152-159, July 1973.

5. Breuer М. А., (Ed.), Design Automation of Digital Systems: vol. I, Theory and Techniques, Prentice-Hall, 1972, имеется русский перевод: Теория и методы автоматизации проектирования вычислительных систем, Брейер М., ред., изд-во Мир , М., 1977.

6. Breuer М. А., Recent Developments in the Automated Design and Analysis of Digital Systems, Proc. IEEE, vol. 60, pp. 12-27, January 1972.

7. Fisk C. J., Caskey D. L., West L. E., ACEL: Automated Circuit Card Etching Layout, Proc. IEEE, pp. 1971-1982, November 1967.

8. Garside R. C Nicholson T. A. J., Permutation Procedure for the Backboard-Wiring Problem, Proc. lEE, vol. 115, pp. 27-30, 1968.

9. Geyer J. M., Connection Routing Algorithm for Printed Circuit Boards, IEEE Trans, on Circuit Theory, vol. CT-19, pp. 95-100, January 1972.

10. Gilbert E. N., Pollak H. O., Steiner Minimal Trees, /. SIAM, vol. 16, pp. 1-29, January 1968.

11. Gilmore P. C, A Solution to the Module Placement Problems, IBM Report RC430, April 1951.

12. Hanan M., Net Wiring for Large Scale Integrated Circuits, 1ВЛ1 Research Report RC-1375, February 1965.

13. Hanan M., On Steiners Problem with Rectilinear Distance, /. SMM, vol. 14 pp. 255-265, March 1966.

14. Hanan M., Kurtzberg J. M., A Review of Placement and Quadratic Assignment Problems, IBM Report RC-3046, April 1970.

15. Haspel H., Automatic Packaging of Computer Circuity, IBM Technical Report TR 00.1295, July 9, 1965.

16. Hightower D., A Solution to Line Routing Problems on the Continuous Plane, Proc. Design Automation Workshop, pp. 1-24, 1969.

17. Hitchcock R., Cellular Wiring and the Cellular .Modeling Technique, Proc. Design Automation Workshop, pp. 25-41, 1969.

18. Kernighan B. W., Lin S., An Efficient Heuristic Procedure for Partitioning Graphs, BSTJ, vol. 49, pp. 291-307, February 1970,

19. Kruskal J. В., Jr., On the Shortest Spanning Subtree of a Graph and the Traveling Salesman Problem, Proc. Am. Math.. Soc, vol. 7, pp. 48-50, 1956.

20. Lawler E. L., Electrical Assemblies with a Minimum Number of Interconnections, IRE Trans, on Electronic Computers, vol. EC-11, pp. 86-88, February 1962.

21. Lawler E. L., Levitt K. N., Turner J., Mo.dule Clustering to Minimize Delay in Digital Networks, IEEE Trans, on Computers, vol. C-18, pp. 47-75, January 1969.

22. Lee C. Y., An Algorithm for Path Connections and Its Applications, IRE Trans, on Electronic Computers, vol. EC-10, pp. 346-365, September 1961.

23. Loberman H., Weinberger A., Formal Procedure for Connecting Terminals with Alinimum Total Wire Length, JACM, vol. 4, pp. 428-433, October 1957.

24. Lodi E., Luccio F., Hypergraph Decomposition with Minimal Connections (не опубликовано).

25. Luccio F., Sami M., On the Decomposition of Networks in Minimally Interconnected Networks, IEEE Trans. Circuit Theory, vol. CT-16, pp 184- 188, May 1969.

26. Mah L., Steinberg L., Topologic Class Routing for Printed Circuit Board Design, Proc. Design Automation Workshop, pp. 80-93, 1972.

27. Moore E. F., Shortest Path Through a Maze, Annals of the Computation Laboratory of Harvard University, vol. 30, pp. 285-292, 1959.

28. Munkres J., Algorithms for the Assignment and Transportation Problems, /. SIAM, vol. 5, pp. 32-38, March 1957,

29. Prim R, C, Shortest Connection Networks and Some Generalizations, BSTJ, vol. 36, pp. 1389-1401, November 1956.

УПРАЖНЕНИЯ

7.1. Пусть (Tl, Ts, Tp) - совокупность допустимых множеств, определяющих допустимое разбиение схемы С. Пусть также N{Ti) - число сетей, связанных с Tt, и Ri -общее число различных сетей С. Покажите, что об-

щее число соединений определяется как 2j (1) - .п^-

7.2. Сформулируйте каждую из следующих задач разбиения в виде задачи целочисленного программирования:

а) Схема содержит соединения с двумя зажимами, дублирование элементов не допускается, каждый модуль содержит не более М элементов; требуется минимизировать общее число промежуточных соединений.

б) То же, что и а), но число выводов в модуле должно быть не больше Р.

в) То же, что и б), ио допускается дублирование элементов.

г) Тоже, что и в), однако сети могут иметь больше двух зажимов.

7.3. Для предотвращения зацикливания в алгоритме Кернихана - Лина (процедура 7.1) каждый элемент переставляется не более одного раза. Другим способом предотвращения зацикливания является запрещение перестановок, не уменьшающих общую цену. Пример 7.2 показывает, что первый метод предотвращения зацикливания может улучшить окончательное разбиение. Приведите пример, показывающий, что и другой механизм предотвращения зацикливания приводит к лучшему решению, или покажите, что это невозможно.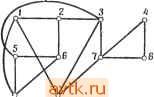

9 10

Рис. 7,50. К упражнению 7.4.

7.4. Для схемы рис. 7.50 примените процедуру 7.2 для нахождения оптимального двухблочного разбиения (4 ТИ 6, где М - число элементов в блоке) для каждого из следующих исходных разбиений:

а) (12345, 678910),

б) для произвольно выбранного разбиения,

в) для разбиения, полученного с помощью процедуры 7.3.

г) для разбиения, полученного с помощью процедуры 7.4.

30. Russo R. L., Oden P. Н., Wolff P. К., A Heuristic Procedure for the Partitioning and Mapping of Computer Logic Graphs, IEEE Trans. On Computers, vol. C-21, pp. 1455-1462, December 1971.

31 Rutman R. A., An Algorithm for Placement of Interconnected Elements Based on Minimum Wire Length, Proc. SICC, pp. 477-491, 1964.

32 Steinberg L., The Backboard Wiring Problem: A Placement Algorithm, SIAM Review, vol. 3, pp. 37-50, 1961.

33. Stone H. S., An Algorithm for Modular Partitioning, /ЛСМ, vol. 17, pp. 182-195, January 1970.

7.5. Для графа, изображенного на рис. 7.51, найдите разбиение, минимизирующее задержку при том условии, что каждый модуль содержит не более 4 элементов (и веса всех элементов равны 1).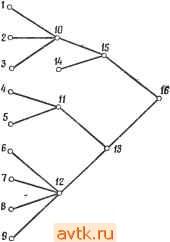

Рис. 7.51. К упражнению 7.5.

7.6. Модифицируйте каждую из процедур 7.1, 7.3, 7.4 в случае, когда разрешено дублирование элементов.

7.7. а) Ниже приводится матрица соединений С и матрица расстояний D; требуется, используя процедуру 7.7В, найти нижнюю граничную оценку общей цены оптимального размещения при заданном частичном размещении

б) Используйте процедуру 7.8В для частичного размещения

(1 2 )

в) Используйте метод ветвей и границ для нахождения оптимального размещения при заданном частичном размещении

7.9. а) Определите размещение для схемы, изображенной на рис. 7.52, при исходном размещении, полученном в б). Используйте две итерации алгоритма (т. е. примените алгоритм к первому полученному решению при другом множестве несоединенных вершин).

б) Получите исходное размещение, используя процедуру 7.12.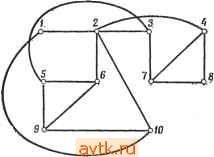

Рис. 7.52. К упражнению 7.9.

7.10. Докажите что для алгоритма Манкреса после каждой итераций сумма всех элементов матрицы размерности (пХп) уменьшается на п{п - пц)к, где ftft -число всех элементов множества S, являющегося множеством строк и столбцов, покрывающих все нули исходной матрицы, а h - наименьший элемент матрицы, принадлежащий строкам или столбцам множества S.

7.11. Используя процедуры 7.13 и 7.14, найдите минимальное дерево покрытий для множества точек сетки (рис. 7.53).

7.12. Для множества точек, отмеченных на рис. 7.53, четырьмя разными способами постройте дерево Штейнера, используя процедуру 7.15.

7.13. а) Обобщите лемму 7.10 для случая, когда можно построить мини мальное дерево для множества {щ, Пг, ..., Пр} вершин при условии исполь зования не более одной (?-вершины.

б) Справедлива ли лемма 7.10, если при построении дерева Штейнера минимизируется евклидово, а не прямоугольное расстояние? Если да - докажите, в противном Случае приведите пример.

7.14. Приведите схему, для которой можно провести трассировку соединений при помощи алгоритма Ли, используя при этом следующие правила упорядочения;

а) самый короткий провод - первоочередной.

б) правило объемлющего прямоугольника.

7.8. Используя алгоритм Манкреса, найдите оптимальное решение (перестановку) для следующей матрицы:

Рпс. 7.53. К упражнению 7.11.

построения цепочки соединений минимальной длины эквивалентны в том смысле, что любой алгоритм, пригодный для решения одной из задач, может быть использован и для решения другой.

7.18. Покажите, что для минимального дерева Штейнера на множестве вершин Ль П2, Пр требуется не более (р - 2) -вершин. (Указание: воспользуйтесь леммой 7.9.)

7.19. Пусть L - длина минимального евклидового дерева Штейнера для планарного множества точек tii, Пг, п-р, Z, -длина минимального дерева Штейнера для того же множества точек, L и L - длины минимального дерева покрытий для того же множества точек в случае соответственно евклидова и прямоугольного расстояний. Найдите граничные оценки для следующих отношений:

L L L и

IF ТГ 77 L

7.20. а) На многослойной плате необходимо проложить соединения Ci, Сг, Ср. Требуется определить число k слоев платы, позволяющее избежать пересечений. Можно ввести в рассмотрение граф пересечений, каждая вершппа i которого представляет соединение С,-, а между вершинами i и / проводится дуга, если вершины i и у нельзя соединить в пределах того же слоя, не образовав пересечений. Хроматическим числом графа G назовем

7.15. Докажите, что при евклидовом расстоянии каждая вершина минимального дерева покрытий имеет не более 6 соединений.

7.16. Справедливо ли следствие 7.1, если рассматривается евклидово расстояние?

7.17. Задача коммивояжера формулируется следующим образом: для заданного множества вершин tiz, ..., Пр} найти цикл минимальной длины, соединяющий все вершины. Докажите, что задача коммивояжера и задача