рассмотрены алгоритмы получения минимальных деревьев покрытий и деревьев Штейнера для произвольных планарных множеств точек.

Минимальные деревья покрытий

Минимальным деревом покрытий данного множества вершин называется граф, соединяющий все вершины и минимизирующий общую длину соединяющих их дуг. Для построения минимальных деревьев покрытий существуют относительно простые конструктивные процедуры [29].

Процедура 7.13

1. Выбираем произвольную вершину i и соединяем ее с некоторой ближайшей к ней вершиной / (т. е. не существует вершины, более близкой к i, чем вершина /, хотя могут быть и другие равноудаленные вершины. Если d{i, /) обозначает расстояние между вершинами i и /, то для всех k d{i, j) d{i, k)).

2. Выбираем несвязную вершину k, для которой mm{d(p, k)). по всем вершинам р, соединенным ранее, минимален. Повторяем указанное действие до тех пор, пока все вершины не будут соединены.

Пример 7.16. Рассмотрим множество из шести вершин со следующей таблицей расстояний:

Выбирая наугад вершину А в качестве исходной, определяем, что ближайшими к ней являются вершины В и С. Соединяем вершины Л и В. Поскольку d{B, С) = 1, минимум mm[d{A, k), d{B, k)] достигается при k = С. Поэтому соединяем вершину В с вершиной С. Аналогичным образом соединяем далее вершину В с Е (или F), затем В с F и, наконец, D с F. Общая длина дуг результирующего графа будет равна

diA, B) + d(B, C) + d{B, E) + d{B, f) + d(D, F) = = 2 + 1 +2 + 2 + 2 = 9.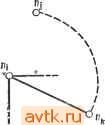

Рис. 7.31. К доказательству леммы 7.5.

одна вершина % этого множества соединена цепочкой дуг с rij (как показано на рис. 7.31,а пунктирной линией), поскольку все без исключения вершины соединены деревом покрытий. Рассмотрим теперь дерево, получаемое при замене дуги между Пг и щ на дугу между щ и rij в соответствии с рис. 7.31,6. Полученный граф также является деревом покрытий (поскольку щ и % по-прежнему соединены между собой через вершину tij, и так как tij является ближайшей к щ вершиной, а не является, то d(ni, rij) = d{ni, rik)- б, где 6 > 0. Следовательно, если изображенное на рис. 7.31,0 дерево имеет общую длину соединений L, то у дерева на рис. 7.31, б длина соединений равна L - б, откуда следует, что исходное дерево не является минимальным деревом покрытий. Полученное противоречие доказывает лемму.

Доказательство этой леммы обосновывает шаг 1 процедуры 7.13 в том случае, если ближайшая из соседних вершин единственна. Для обоснования шага 2 той же процедуры нам понадобятся следующие определения.

Пусть необходимо построить минимальное дерево покрытий для множества из р вершин ni, tiz, tip. Назовем фрагментом подмножество соединенных между собой вершин этого множе-

Для доказательства того, что эта процедура всегда обеспечивает получение минимального дерева покрытий, докажем ряд следующих лемм.

Лемма 7.5. Для получения минимального дерева покрытий на множестве верщин { ь г, - ., tip} каждая вершина должна быть непосредственно соединена по крайней мере с одной соседней вершиной.

Доказательство. Предположим, что вершина п,- не соединена непосредственно ни с одной из соседних вершин, и допустим, что ближайшей к ней вершиной является щ. Тогда щ соединена с некоторым непустым множеством вершин и по крайней мере

a б в

Рис. 7.32. К доказательству леммы 7.7.

Доказательство. Предположим, что для множества вершин { 1 Пр} с расстояниями d(n,-, Uj) существует минимальное дерево покрытий с общей длиной дуг, равной L. Допустим теперь, что при построении дерева покрытий с помощью процедуры 7.13 нашелся фрагмент, имеющий два ближайших соседа ki и kz, на расстоянии d (т.е. d{nu ki) = d( 2, Аг) = d, где П\ и Пг принадлежат одному фрагменту и, в частности, щ и Пг могут совпадать). Эта ситуация поясняется рис. 7.32, а. Рассмотрим теперь случай, когда дуга между ni и ki укорачивается до d - е (рис. 7.32,6) или удлиняется до d + е (рис. 7.32,б), в то время как .длины других дуг не изменяются.

Е графе 7.32,6 рассматриваемый фрагмент соединен с вершиной k\, что соответствует построению минимального дерева покрытий длины и, где L - е L L (так как длина минимального дерева покрытий не может увеличиться из-за уменьше-

ства. Ближайшим соседом фрагмента F, содержащего вершины Пи 2, . назовем вершину Пи, такую, что ПифР и для некоторой вершины ПгР, (1{пиПи)с1\п^,Пт) для всех Щ^Р и ПтфР (т. е. п - не содержащаяся в этом фрагменте вершина, которая минимизирует min(d,(nj, п^)) по всем вершинам tii фрагмента).

Лемма 7.6. В минимальном дереве покрытий, построенном на вершинах {щ, 2, ., п-р}, каждый фрагмент должен быть непосредственно соединен по крайней мере с одним ближайшим соседом.

Доказательство. Аналогично доказательству леммы 7.5, но вместо вершины щ следует рассматривать фрагмент, состоящий из множества вершин { ь 2, , п^.

Это обосновывает процедуру 7.13 при условии, что все расстояния различны. В противном случае, как доказано в следующей лемме, может быть выбран любой из ближайших соседей.

Лемма 7.7. Если у данной вершины (или фрагмента) более одного ближайшего соседа, то при построении минимального дерева покрытий соединение может быть проложено к любому из них.

Щ к, щ к, п, kt

НИЯ длины одной из дуг), в графе на рис. 7.32,6 рассматриваемый фрагмент соединен с вершиной Аг, а длина полученного минимального дерева покрытий равна L , где L L L -f е. Но в пределе при и L равны, а следовательно, оба гра-

фа являются минимальными деревьями покрытий. В заключение доказательства заметим, что такие же рассуждения справедливы и в случае, когда число ближайших соседей больше двух.

При использовании процедуры 7.13 для построения на прямоугольной сетке минимального дерева покрытий может возникнуть следующая сложность. Предположим, что по любому отрезку сетки Допускается прокладка не более одного соединения,

при этом у каждой вершины получается не более четырех соединений. Однако в терминах прямоугольного расстояния некоторая вершина может оказаться ближайшим соседом более чем четырех вершин. Так, например, вершина А на рис. 7.33 является ближайшим соседом восьми других изо-браженых на рисунке вершин.

Если у вершины только четыре ближайших соседа, то их можно соединить с ней вертикальными и горизонтальными путями минимальной длины. Вершины В, G, Н и I, например, находятся на расстоянии 2 от вершины А. Однако для их непосредственного соединения с вершиной А не достаточно провода общей протяженностью 9 единиц. Минимальное дерево покрытий образуется в этом случае соединением вершин А, В, G и Я с вершиной /. Из этого примера ясна необходимость правильного выбора путей, используемых для построения деревьев покрытий, при реализации соединений схемы.

При наличии п вершин сложность процедуры 7.13 определяется для худшего случая следующим образом. На первом шаге сравниваются длины п - 1 дуги. Если фрагмент графа содержит k дуг, то число необходимых сравнений равно k{n-k). Тогда общее число сравнений во всех итерациях равно

Е i{n-i).

Рис. 7.33. Пример вершины, являющейся ближайшим соседом восьми других вершин.

Общее число необходимых сравнений можно уменьшить. Пусть й{щ. Пи) обозначает расстояние между вершинами и Пи, а через Fi обозначен фрагмент, содержащий i вершин, полученных после i- 1 итераций рассматриваемой процедуры.

В конце г-й итерации мы заменяем с1{п Пи), где щ^Рг и ПифРг, на минимальное расстояние до фрагмента Ри т.е. на min [d{ni, Число необходимых для определения мини-

г Pi

мального расстояния от каждой несоединенной вершины до этого фрагмента сравнений на (г- 1)-й итерации равно {п - г). Это означает, что минимальное расстояние от каждой данной вершины до фрагмента, полученного на (г - 1)-й итерации, должно сравниваться с расстоянием от этой вершины до последней включенной в фрагмент вершины. Для выбора вершины, включаемой во фрагмент на 1-й итерации, требуется (п -г-1) сравнение. Следовательно, общее число необходимых сравнений

равно 2] (2 - 2г'-1), а вычислительная сложность пропор-(=1

циональна п^.

Для образования минимального дерева покрытий можно использовать и другую процедуру. Процедура 7.14

1. Упорядочиваем в порядке возрастания длины все дуги, выбираем из них наиболее короткую (если их несколько, то выбираем любую из них) и соединяем соответствующие вершины, связанные этой дугой.

2. На каждой последующей стадии отбираем наиболее короткую дугу до тех пор, пока среди соединенных вершин не образуется замкнутого цикла. В этом случае последняя из рассмотренных дуг исключается. Правильность этой процедуры следует непосредственно из лемм 7.5-7.7.

Пример 7.17. Для рассмотренного в примере 7.16 множества из шести вершин ниже перечислены длины соответствующих дуг:

Первой выбирается самая короткая дуга, это дуга между верщинами В и С, длина которой равна 1. Далее из дуг длины 2 (таких дуг всего пять) произвольным образом выбирается одна,

пусть это будет дуга, соединяющая вершины А и В. Дуга между А и С исключается, поскольку иначе образуется замкнутый цикл, состоящий из вершин А, В я С, т.е. граф перестает быть деревом. Далее мы выбираем дуги, соединяющие соответственно В и Е, В и F, D и F, после чего построение дерева заканчивается. Полученное минимальное дерево покрытий идентично полученному в примере 7.16, длина дуг этого дерева равна 9. Другим минимальным деревом покрытий является дерево, содержащее дуги, которые соединяют вершины В и С, А а С, В и Е, В и F, DhF.

Деревья Штейнера

Рассматриваемая задача усложняется, если при соединении множества вершин допускается использование дополнительных точек соединения. Возникающую задачу, называемую часто задачей Штейнера, можно сформулировать так: для заданных р точек плоскости построить соединяющее их дерево с р вершинами, общая длина ветвей которого минимальна. Поскольку обычно используются соединения прямоугольной конфигурации, мы ограничимся рассмотрением прямоугольного расстояния. Для нахождения решения задачи Штейнера при р 5 требуется разумный объем вычислений, в общем случае могут быть получены лишь соответствующие условия, которым должны удовлетворять деревья Штейнера.

Обозначим исходные р вершин через Пи г, .., Пр, а дополнительные вершины (соединительные точки), называемые точками Штейнера, будем обозначать буквой q с различными индексами.

Лемма 7.8. Пусть G является деревом Штейнера для р вершин i, Пг, ..., Пр. Если G содержит т вершин и является связным подграфом графа G, то G является деревом Штейнера для этих т вершин.

Доказательство. Если G не является деревом Штейнера для этих т вершин, заменим его на G - подграф, являющийся деревом Штейнера для этих вершин. Полученный граф содержит р исходных вершин, но суммарная длина его дуг меньше, чем у графа G, следовательно, G не является деревом Штейнера для вершин П\, П2, Пр. Получено противоречие.

Пусть каждая из р вершин ь г, , р заданного множества имеет координаты (х,-, yi). Положим

гаах = тахл:г, У„,ах ==maxy,-, i i

Хмп = rain Xi, Ymin == min yi.

Тогда все р вершин могут быть заключены в прямоугольник со следующими координатами вершин:

(.niln, mln), (.mln, гаах), (max, mln), (.raax> max)-

Назовем этот прямоугольник минимальным объемлющим прямоугольником для этих р вершин и обозначим через R (щ, Пг, ...

Пр). На рис. 7.34 изображен минимальный объемлющий прямоугольник для множества из шести вершин, отмеченных на рисунке крестиками.

Следующая последовательность лемм и теорем дает необходимые условия существования и построения деревьев Штейнера.

Лемма 7.9. Пусть заданы р вершин, которые должны быть соединены между собой. Для них всегда можно построить дерево Штейнера, в котором каждая дополнительная вершина Qi (точка Штейнера) соединена по крайней мере с тремя другими.

Доказательство. Допустим, что дополнительная вершина Qi дерева Штейнера соединена только с двумя вершинами (рис. 7.35, а). Удалим вершину qt и обе соединенные с ней дуги и соединим между собой две вершины, которые были связаны

Рис. 7.34. Минимальный объемлющий прямоугольник.

Рис. 7.35. К доказательству леммы 7.9.

С qi (рис. 7.35,6). Полученный граф по-прежнему является деревом Штейнера, поскольку расстояние между двумя вершинами не превосходит суммы расстояний между ними и третьей вершиной ).

Лемма 7.10. Для данного множества вершин {пь 2, з}. которые должны быть соединены с вершиной с координатами (xi. У}), координатами точки q, минимизирующей

) Что справедливо и для прямоугольных расстояний.-~ Яркж. ред.

Ё d (q, ni) (где d [q, щ) -- прямоугольное расстояние между q

и щ), будут (Хер, Уср). где Хер -среднее значение Xt, i = l, 2, 3,

и Fcp -среднее значение г/г==1, 2, 3, а Ц^С?, Л =

= Ч2Р{Я{пи 2, Пз)), где P(i?) обозначает длину периметра R.

Доказательство. Предлагается провести самостоятельно.

Пример 7.18. Для множества {пи г, з} трех вершин (рис. 7.36) показана минимизирующая d{q, п,) точка Штейнера q.

Лемма 7.11. Пусть G - дерево Штейнера множества из р точек плоскости. Пусть q является -вершиной, соединенной с тремя и только тремя вершинами [аи аг, аз) (эти вершины могут быть как исходными, так и д-вершинами). Тогда 1) q находится внутри R{au Иг, Сз)-объемлющего прямоугольника, определяемого точками аи а^, з; 2) внутри R{au аг, йз) -вершина единственна.

Доказательство. 1. Пусть G является деревом Штейнера. Рассмотрим подграф, состоящий из вершин аи а% az, q. Если точка имеет координаты {Xi, Уг), то для обеспечения минимума суммы расстояний от точки q до других точек координаты (Хер, Fcp) точки q должны удовлетворять условиям лемм 7.8 и 7.10. Следовательно, q находится внутри R {аи аг, аз). 2. Допустим, что внутри R{au аг, аз) находится другая вершина Ui с координатами (4, yi). Тогда й4 должна быть соединена по крайней мере с одной из вершин {аи аг, аз) путем, не проходящим через q, поскольку G является деревом, а вершина q соединена только с аи аг и а^. Пусть, например, щ соединена с ai (рис. 7.37,а). Рассмотрим поддерево, образующееся при перенесении^ в точку с координатами(Х^р, Fp), где Х^р--среднее значение х^, х^, х^, а Fp-среднее значение уг, уз, У4, и соединим q с аг, аз, ai (рис. 7.37, Ь). Поскольку й4 находится внутри объемлющего прямоугольника R{au аг, аз), прямоугольник Р'(й2. 3. Й4) принадлежит R{au аг, аз), а значит, l2P{R)<.hP{R). Далее рассматриваемое поддерево соединяется с остальной частью графа путем от щ до аи Следовательно, новый граф G является деревом с меньшей суммарной длиной дуг, чем у графа G (разность суммарных длин равна

Рнс. 7.36. Оптимальное размещение р-точки

а б

Рис. 7.37. К доказательству леммы 7.11.

Предлагается доказать, что для множества из р вершин существуют не более (р - 2) -вершин.) Следствие выводится с помощью лемм 7.10 и 7.11.

Пусть на плоскости заданы точки {щ, П2, Пр}. Если через каждую из них провести линии, параллельные осям ж и у, на плоскости образуется сетка. Обозначим через / множество точек пересечения линий сетки, при этом оно содержит и множество исходных точек. Число дополнительно полученных точек не превосходит при этом р2 - р. Ряд следующих лемм доказывает существование для любого множества вершин на плоскости дерева Штейнера, все -вершины которого принадлежат множеству /.

Лемма 7.12. Пусть G является деревом Штейнера для множества {пи Пр) вершин, а -вершины этого дерева образуют множество Q. Если Qi - множество -вершин, не принадлежащих множеству /, то оно содержит элемент q, соединенный не менее чем с двумя вершинами из / (считая и п-вершины) или множество Qi пусто.

Доказательство. Предположим, что Qi не является пустым множеством и все вершины Q\ соединены не более чем с одной вершиной из множества /. Число вершин, соединенных с w{qi) 3 для всех / (согласно лемме 7.9). Рассмотрим подграф.

С/г) (Р(Р) - Р())- Это противоречит предположению о том, что G является деревом Штейнера.

Следствие 7.1. Для данного множества {пь пг, Пз} точек плоскости дерево Штейнера содержит одну -вершину с координатами (Хер, Уср) (если она не совпадает ни с одной из вершин 1, 2. з). а суммарная его длрша равна {}1%)Р{,Я{пиП2,Пъ)).

Доказательство. Из леммы 7.9 следует существование не более одной -вершины. (В качестве самостоятельного упражнения

определяемый вершинами множества Qu и обозначим через E{Qi) число вершин этого подграфа. Каждая вершина qiQx соединена не менее чем с w{qi)- 1 вершинами из Qi, поскольку предполагается, что она соединена не более чем с одной вершиной из множества /. Следовательно,

где Й1 -число вершин множества Qu Но максимальное число дуг дерева, имеющ.его ki вершин, равно ftj - 1. Откуда следует, что в этом педграфе должен существовать замкнутый цикл, а следовательно, G не является деревом Штейнера. Получено противоречие.

Лемма 7.13. Пусть G является деревом Штейнера для множества вершин {пи Пу) и -вершины этого дерева образуют множество Q. Пусть Qi - множество -вершин, не принадлежащих /, а элемент qi из множества Qi соединен с двумя точками il, t2 Е /. Тогда можно построить дерево Штейнера G, отличное от G, которое не содержит вершину qi и любая вершина Qj которого, соединенная с k и t2, принадлежит множеству /.

Доказательство. На основании леммы 7.9 w{qi) 3. Предположим сначала, что w{qi)-= 3. Пусть вершина qi соединена с iu 12 и аи Если aiI, то на основании леммы 7.8 и следствия 7.1 qi е /. Таким образом, qi ф1, ai I, т. е. ai е Qu

Согласно лемме 7.8 и следствию 7.1, хотя бы одна из вершин il или t2 должна находиться на горизонтали или вертикали, проходящих через точку qu Без ограничения общности можно предположить, что il находится на проходящей через qi горизонтали. Далее, одна из вершин iu 12, ai должна находиться на одной вертикали с точкой qu Поскольку qiI, в то время как ii и 12 принадлежат /, ai должна быть на одной вертикальной линии с 1, а расположение iu 2 и ai должно соответствовать рис. 7.38, а.

Далее, в силу того, что точка ai ф I, она является -вершиной и должна быть соединена по крайней мере с двумя другими точками. Согласно лемме 7.8 и следствию 7.1, по крайней мере одна из этих двух точек, например аг, должна находиться на одной горизонтали с аи Можно рассматривать два случая: 1) точка аг находится справа от t2 и 2) аг расположена левее 1г.

Случай 1 иллюстрируется рис. 7.38,6. Изображенный на рис. 7.38,6 граф G получен при помощи сдвига линии, соединяющей qi и аи Этот граф не содержит вершину qu но содержит вершину q\ I. Суммарная длина дуг у графа G та же, что и у графа G, а значит, он является деревом Штейнера.