Перестановка элементов 4 и 1 приводит к размещению, имеющему цену, равную 15, которое не может быть улучшено последующими итерациями (рис. 7.24, б).

Эта процедура не будет зацикливаться, поскольку действия прекращаются, как только не остается перестановок, приводящих к уменьшению общей длины соединений. В другом варианте этой процедуры перестановки продолжаются по локально-оптимальному принципу, даже если цена возрастает. Для предотвращения зацикливания ни одна вершина, на которой уже

Рис. 7.24. Улучшенное размещение (а) и размещение, полученное после

второй итерации (б).

была основана предшествующая перестановка, больше не перемещается. В заключение из всех полученных размещений, как и в процедуре 7.1 для решения задачи о разбиении, выбирается размещение, имеющее наименьшую цену.

В другой итеративной процедуре [32] рассматриваются перестановки элементов из множества непосредственно не соединенных между собой элементов. Рассмотрим исходное размещение М элементов на плате с N М позициями. Пара элементов i и /, не соединенных непосредственно между собой, называется несвязной парой элементов. Множество элементов, в котором любая пара является несвязной, называется несвязным множеством. Множество несвязных элементов является максимальным, если каждый элемент, не содержащийся в нем, непосредственно соединен хотя бы с одним из элементов множества. Для образования максимальных несвязных множеств элементов может быть использована следующая простая процедура.

Процедура 7.10 - j

Г.Выбираемнекоторый элементе! и полагаем Scsfei}.

2. Выбираем некоторый элемент еч, не связанный непосредственно ни с одним элементом е S, и включаем его в S.

3. Повторяем шаг 2 до тех пор, пока ни один элемент нельзя будет добавить к множеству S. Множество 5 будет, таким образом, максимальным несвязным множеством.

Очевидно, можно образовать различные максимальные множества несвязных элементов. Перестановка элементов этих несвязных множеств является основой другой приближенной итеративной процедуры.

Процедура 7.11 [32]

1. Для данного исходного размещения образуется максимальное множество несвязных элементов; эти элементы убираются, что приводит к образованию N -- М -\- Р свободных позиций на плате, где Р - число элементов несвязного множества.

2. Рассматривается некоторый элемент вг множества несвязных элементов и помещается в некоторую позицию Pj. Поскольку этот элемент не соединен с другими удаленными элементами, общая длина соединений элемента е,-, помещенного в позицию Pj, может быть вычислена независимо от размещения остав-щихся элементов.

3. Шаг 2 повторяется для каждого из Р элементов, и для - М.-\-Р ячеек образуется, таким образом, матрица Р y.{N - М \-Р), элементом ц которой является величина, характеризующая увеличение протяженности соединений (или общий вклад) в результате размещения элемента е, в позиции Pj.

4. Из этой матрицы определяется размещение множества Р элементов в N - М -\- Р позициях, минимизирующее общую протяженность несвязного множества. Длина соединений между элементами, не входящими в несвязное множество, остается постоянной, поскольку сами они не перемещаются. Следовательно, оптимальное размещение несвязного множества соответствует оптимальной перестановке для этой матрицы, которая может быть найдена с помощью процедуры 7.9.

5. Указанные действия повторяются для различных исходных размещений и/или различных максимальных множеств несвязных элементов. Для последующих итераций в качестве исходных размещений могут использоваться решения, полученные на предшествующих итерациях.

Пример 7.14. Для схемы, изображенной на рис. 7.25, а, рассмотрим исходное размещение, соответствующее рис. 7.25, в (то же, что и в примере 7.13), с максимальным связным множеством элементов {1,2,3,4}.

Определим теперь матрицу, строки которой соответствуют элементам 1, 2, 3, 4, столбцы соответствуют позициям 2, 3, 4, 6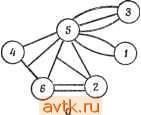

Рис. 7.25. Схема (а), разметка позиций платы (б) и исходное размещение (е)

вершин. В следующем разделе обсуждаются различные ограничения на такие соединения. В данном примере мы предполагаем, что вершины соединяются с ближайшими соседними.) Результирующей матрицей является

Для нахождения размещения с минимальной ценой сначала нормализуем матрицу. В результирующей матрице (показанной

(где позиции перенумерованы в соответствии с рис. 7.25,6), а каждый элемент соответствует цене размещения данного модуля в данную позицию. (Для сетей с несколькими внешними зажимами цена зависит от того, как соединено данное множество

Рис. 7.26. Окончательнсе размещение (пример 7.14).

1 В 4, 2 В Рб, 3 В Рг и 4 В Рз. Цена иллюстрируемого на рис. 7.26 решения равна 18.

1 2 3 4

в процедуре 7.11 находится оптимальное решение при том ограничении, что элементы, которые не были перемещены на первом шаге, должны оставаться на своих исходных местах.

©

© ©

Рис. 7.27. Неудачное размещение.

Однако в общем случае перестановка несвязных множеств элементов может не привести к улучшению некоторых заведомо неудачных размещений. В качестве примера рассмотрим размещение, показанное на рис. 7.27, для которого уменьшение длины соединений не может быть достигнуто при помощи переста-

ниже) есть четыре нулевых элемента, которые можно использовать для определения оптимального размещения: это элементы

новок только несвязных элементов А и С или В и D. Тем не менее размещение может быть определенным образом улучшено путем перестановки элементов А и В. Однако, если можно переставлять местами только несвязные элементы, такая перестановка является недопустимой. Следовательно, помимо перестановок несвязных элементов может оказаться желательной перестановка и соединенных между собой элементов. (Для облегчения этого рассмотренный алгоритм может быть модифицирован таким образом, чтобы сначала производилась минимизация длины наиболее длинных соединений путем парных перестановок или на основе какого-либо другого метода.)

Из сказанного понятно, что эффективность итеративных процедур сильно зависит от используемого исходного размещения. Для получения приемлемых исходных размещений используются конструктивные эвристические методы.

7.6Л КОНСТРУКТИВНЫЕ МЕТОДЫ РАЗМЕЩЕНИЯ

Конструктивные методы размещения представляют собой упорядоченный выбор размещаемых элементов; при этом порядок размещения определяется при помощи некоторого правила выбора, а позиция размещения определяется на основе вычисления целевой функции. Однако оптимальную ячейку для размещения выбранного элемента точно определить нельзя, поскольку ее определение может зависеть от позиции некоторых еще не размещенных элементов. Общим принципом является попытка разместить множества сильносвязных элементов. При этом возможен следующий подход.

Процедура 7.12

1. Выбирается элемент, имеющий наибольшее число соединений, и размещается в центре платы.

2. В качестве следуюш.его элемента выбирается элемент, обусловливающий наименьшее увеличение (или наибольшее уменьшение) числа соединений между множества.ми размещенных и неразмещенных элементов. Согласно этому правилу выбора, пучки сильносвязных элементов размещаются последовательно, в то время как соседние ячейки в значительной степени остаются свободными. (В случае неоднозначности выбирается элемент, имеющий наибольшее число путей передачи сигналов.)

3. Выбранный элемент размещается таким образом, чтобы минимизировать длину его соединений с ранее размещенными модулями. Для этого вычисляется центр тяжести уже размещенных элементов, с которыми должен быть соединен новый элемент. Это значит, что, если имеет да,- соединений с элементом бг, размещенным в ячейке (х,-, г/j), г = 1 ... k, размещается как можно ближе к точке с координатами {Xj, у^).

где

Неоднозначные ситуации, возникающие при использовании процедуры 7.12 в выборе и в размещении, могут быть разрешены дальнейшим исследованием последствий выбора каждого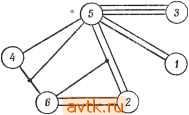

Рис. 7.28. Схема (а) из примера 7.15 и плата для нее (б).

ВОЗМОЖНОГО варианта. Возможно улучшение алгоритма за счет использования более сложной целевой функции. Возможно также обобщение алгоритма, при котором исходный элемент размещается в некоторой начальной области, вокруг которой могут размещаться другие элементы в соответствии с топологией платы. Таким образом, исходный элемент не обязательно помещается в центре платы.

Пример 7.15. Рассмотрим схему, изображенную на рис. 7.28, а, которая должна быть размещена на плате, показанной на рис. 7.28, б.

В соответствии с процедурой 7.12 мы выбираем сначала элемент 5 и размещаем его, как показано на рис. 7.29, а. Следующая таблица показывает для каждого из оставшихся элементов

определяемыми следующим образом:

к

. б

Рис. 7.2&. Решение задачи размещения из примера 7.15.

изменение числа сетей А, соединяющих множества уже размещенных и еще не размещенных элементов, вследствие размещения на следующем шаге элемента i.

1 2 3 4 6

А -2

-3 -1

Выбор элемента 3 приводит к наибольшему уменьшению числа сетей, соединяющих размещенные и неразмещенные элементы. Элемент 3 может быть размещен в позициях Рь или Ps. Заметим, однако, что у позиции Р^ две смежные свободные позиции {Рг и Рб), в то время как у Pi и Р5 по одной смежной свободной позиции. Поскольку элемент 3 соединен только с

Заметим, что соответствующие значения А для этих элементов не изменились. Это можно было предсказать, так как ни один из них не соединен с уже размещенным элементом 3. Выбираем элемент 1 и после аналогичных рассуждений помещаем его в позицию Pg, что приводит к показанному на рис. 7.29,6, частичному размещению.

Можно убедиться, что для остающихся элементов величина А не изменится, поэтому выбирается элемент 4. Поскольку элемент 4 соединен только с элементами 5 и 6, а элемент 6 еще не был размещен, мы помещаем элемент 4 как можно ближе к элементу 5, т. е. в Р4. Пересчитывая значения А для модулей 2 и 6 (поскольку элементы 2 и 4 не соединены, значение А изменится только для элемента 6), получаем

2 6

А

Элемент 6 должен быть размещен в Рг (или, что эквивалентно, в Ре), а элемент 2 в Ре. Цена окончательного размещения равна 18 (рис. 7,29,б).

Для схем с сетями, соединяющими Р > 2 элементов, представляется возможным модифицировать процедуру 7.12: можно считать, что каждый из этих Р элементов имеет 1/(Р- 1) соединений с остальными Р - 1 элементами сети.

Можно показать, что сложность вычислений (или время вычислений) процедуры 7.12 возрастает как ЛР, где М - число размещаемых элементов, т. е. эта процедура применима на практике. Цена (длина соединений) полученного решения (так же как и время вычислений) может зависеть от сложности процедур прогнозирования, используемых при разрешении неоднозначных ситуаций, возникающих при выборе и размещении очередного элемента.

7.7. ТРАССИРОВКА

После того как схема (или система) была разбита на части и элементы размещены на платах, необходимо произвести трассировку, т. е. выбрать маршруты соединений между ними. Суще-

элементом 5, мы помещаем элемент 3 в Pi (позиции Pi и Pg эквивалентны в силу симметрии). Теперь мы пересчитаем значения А для неразмещенных элементов.

12 4 6

7.7.1. ВЫБОР СОЕДИНЕНИЙ

Каждая сигнальная сеть определяет множество элементов, которые должны быть соединены друг с другом. Однако в зависимости от технологии к сетевым сеединениям могут предъявляться различные требования, такие, как ограничение числа проводов, связанных с одним выводом, с запрещением использования точек вспомогательных соединений; возможность введения точек вспомогательных соединений, обеспечивающих уменьшение цены проводки.

Выполнение каждого из этих требований приводит к различным вариантам трассировки. Множество элементов должно быть соединено таким образом, чтобы упростить окончательную трассировку соединений. Из-за отсутствия другого подходящего критерия в качестве общего критерия оптимизации обычно рассматривается минимизация общей длины соединений. Рассмотрим

ствует много физических характеристик, желательных для такой трассировки, которые можно перевести на язык ограничений и критериев оптимизации. Такие распространенные ограничения и критерии перечислены ниже.

1. Элементы должны быть соединены вертикально и горизонтально расположенными проводниками в соответствии с конфигурацией прямоугольной сетки. Выполнение этого ограничения обеспечивает компактное расположение проводов.

2. Между проводами не должно быТь пересечений или число таких пересечений должно быть минимизировано.

3. Общая протяженность проводки должна быть минимизирована.

Задача трассировки состоит из двух частей.

1. Выбор множества соединений (определение списка проводов). Для того чтобы соединить сетью п элементов, не обязательно делать специальные соединения для каждой из g пар

элементов. Сеть из п элементов может быть образована при помощи (п-1) соединения. Для каждой п-элементной сети мы должны выбрать для соединения множество из (п-1) пары элементов.

2. Определение соединительных путей. В соответствии с конструктивными ограничениями и критериями оптимизации для элементов, выбранных на шаге 1, производится трассировка соединений.

Несмотря на то что перечисленные задачи взаимосвязаны, в силу сложности всей задачи в целом мы рассмотрим их по отдельности.

Рис. 7.30. Множество точек, которые должны быть соединены (с); минимальная цепь (б);. минимальное дерево покрытий (е); дерево Штейнера (г).

показанное на рис. 7.30, й размещение. Шесть элементов (отмеченных крестиками) должны быть соединены горизонтальными и вертикальными отрезками изображенной сетки для образования сети. В том случае, когда с одним контактным штырьком (выводом) связано не более двух соединений, говорят о связующей цепи. На рис. 7.30,6 показана минимальная цепь, соединяющая отмеченные точки, длина этой цепи равна 14.

Отсутствие ограничений на число соединений для одного вывода и запрещение использования вспомогательных выводов приводят к конфигурации, называемой деревом покрытия. В нашем примере минимальное дерево покрытий, показанное на рис. 7.30,6, имеет длину, равную 12. В случае когда разрешено использование дополнительных точек соединения, искомая конфигурация называется деревом Штейнера. Дерево Штейнера для показанного на рис. 7.30, й множества вершин изображено на рис. 7.30, г. Общая длина его соединений равна 11, и для него требуется одна вспомогательная точка соединения. Далее будут