Процедура 7.7А

1. Расположить элементы Cij, j > i (т.е. элементы, находящиеся над главной диагональю) матрицы соединений (при необходимости расширенной) в порядке возрастания.

2. Расположить элементы йц, j > t матрицы расстояний в порядке убывания.

3. Перемножить последовательно элементы полученных на первых двух шагах списков (т. е. элемент i первого списка умножить на /-Й элемент второго списка для всех i). Сумма полученных результатов определит нижнюю границу общей длины соединений при оптимальном размещении.

Пример 7.8. Рассмотрим следующие матрицы соединений и расстояний:

г О 2 5 3

2 О 1 О

3-1 О 4 О -J

О 2 3 6

3 2 О 1 4

Поскольку модулей всего четыре, а позиций пять, мы добавляем пятый фиктивный модуль и полагаем = О = cj для всех i и j. Располагаем элементы С в порядке возрастания:

О, О, О, о, о, 1. 2. 3, 4, 5

Элементы D располагаем в порядке убывания:

7, 6, 4, 4, 3, 3, 3, 2, I, 1

Перемножая соответствующие элементы и складывая полученные результаты, получаем (О X 7) + (О X 6) + (О X 4) -f (О X 4) +

+ (0ХЗ) + (1ХЗ) + (2ХЗ) + (ЗХ2) + (4Х1) + (5Х1) = 24,

что и определяет нижнюю граничную оценку.

В процедуре 7.7А при определении нижней граничной оценки не учитывается конкретная структура матриц С (соединений) и D (расстояний). Используются только сами элементы этих матриц. Вот почему результат оказывается слабым в том смысле, что он не соответствует реальному размещению и далек от разумных оценок длины соединений в оптимальном случае. Оба указанных недостатка в процедуре 7.7А можно исключить. Прежде всего определим матрицу Л=(аг,-), где элемент - нижняя граничная оценка минимального вклада в общую протяженность соединений, образующегося при размещении элемента I в /-Й позиции.

Процедура 7.8А. При заданных матрице соединений С (при необходимости расширенной) и матрице расстояний D матрица А = (Uij) получается поэлементно.

Позиция

Элемент щв подсчитывается следующим образом. Упорядочиваются все недиагональные .элементы строки 1 расширенной матрицы С: 0,2,3,5 и все недиагональные элементы строки 5 матрицы D: 7,6,4,3.

Л,5==(0Х7) + (2Х6) + (ЗХ4) + (5ХЗ) = 39.

Размещение модулей (модуль i размещается в позиции p{i)) определяет перестановку, поскольку никакие два модуля не могут располагаться в одной позиции. Тогда нижняя граничная оценка общей протяженности соединений при таком размеще-

НИИ равна (/2) 2] а (множитель /2 необходим в силу того.

что длина соединения между элементами t и / учитывается и в г, р(г), и в Oj, p(j)). Для нскоторой матрицы А размерности (iVX ) перестановка определяется как множество из N элементов А, по одному из каждого столбца и каждой строки. Каждое возможное размещение соответствует некоторой перестановке. Все элементы матрицы А, образуемые с помощью процеду-

Элемент матрицы а - получаем следующим образом:

1. Располагаем недиагональные элементы строки i матрицы С (т. е. Cij, i ф j) в порядке возрастания.

2. Располагаем недиагональные элементы строки / матрицы D (т. е. dij, i ф j) в порядке убывания.

3. Перемножаем соответствующие элементы полученных последовательностей и суммируем результаты. Полученное число и есть Oij.

Пример 7.9. Для матриц С (расширенной) и Z) из примера 7.8 матрица Л имеет следующий вид:

ры 7.8, неотрицательны. Следовательно, в случае если матрица содержит N независимых нулей (но ни в одной строке и ни в одном столбце нет двух нулей), то эти N нулей определяют оптимальное решение с ценой 0. (Нулевой элемент ац показывает, что элемент i помещается в ячейку /.) Можно показать, что если матрица не содержит независимых нулей, то она преобразуется путем сложения и вычитания из элементов ее строки или столбца некоторой постоянной величины таким образом, что обеспечивается увеличение числа независимых нулей. Следующая лемма показывает, что такое преобразование не изменяет оптимального решения, хотя и может изменить цену оптимального решения.

Лемма 7.4. Пусть задана матрица А. Матрица А' образуется вычитанием или прибавлением константы к. из произвольной строки (или столбца) матрицы А. Тогда оптимальная перестановка для А оптимальна и для А'.

Доказательство. Мы проведем доказательство для случая вычитания константы k из г-й строки. Доказательство для столбцов следует из соображений симметрии, а доказательство в случае сложения почти идентично рассматриваемому.

Пусть является оптимальной перестановкой с ценой а для матрицы А. Если не является оптимальной перестановкой для А', то для А' есть оптимальная перестановка kj с ценой а'. Цена Пд для А' равна а - к, поскольку А совпадает с А', за исключением строки г, цена каждого элемента которой была уменьшена на к. Следовательно, а' <.а - к. Но в силу тех же соображений цена для А равна а'+ к. Если а'<,а - к, то а' -\-к <а. Следовательно, зх не является оптимальной перестановкой для А, что является противоречием.

Систематическая процедура преобразования матрицы А к виду, когда преобразованная матрица имеет N нулей (что соответствует оптимуму), сводится к следующим операциям.

Процедура 7.9 (алгоритм Манкреса [28])

1. Для каждой строки i из А выбираем наименьший элемент Gmin и вычитаем Ятш из всех элементов этой строки. Затем в каждом столбце / выбираем наименьший элемент и вычитаем его из каждого элемента столбца j. Эти действия называются нормализацией матрицы. Полученная матрица имеет по крайней мере один нулевой элемент в каждой строке и каждом столбце.

2. В матрице А отыскивается максимальное множество из щ независимых нулей. Если пу = N, то определена оптимальная перестановка. Если щ < Л', то в матрице А выделяется множество S из П1 строк и столбцов, содержащих все имеющиеся нулевые элементы.

Множество S состоит из строки 5 и столбцов 2 и 3, содержащих только нули. Минимальный из не содержащихся в 5 элементов равен 1. Производя сложение и вычитание в соответствии с процедурой 7.9, получаем матрицу:

О

О

I I О О

2 21 -О-5

3 20 2 13

-О-О

Множество S теперь состоит, как это показано, из строк 2, 5 и столбцов 2, 3, а /i = 2. После преобразования результирующая

3. Выбирается наименьший из не содержащихся в 5 элементов А. Этот элемент h прибавляется ко всем элементам каждой из строк и каждого из столбцов S, после чего h вычитается из каждого элемента А. (Заметим, что указанные действия соответствуют вычитанию h из каждого элемента, не покрываемого S, и прибавлению h к элементу, одновременно покрываемому строкой и столбцом S, при том что остальные элементы не изменяются.)

4. Далее шаги 2 и 3 повторяются до тех пор, пока не будет получено решение (т.е. Л' независимых нулей).

Возможность применения описанной процедуры следует из леммы 7.4. На каждой итерации сумма всех элементов матрицы уменьшается на Л'(Л' - щ)Н, где Пп - число независимых нулей. Следовательно, процедура конечна. Можно показать, что один из вариантов этой процедуры имеет вычислительную сложность, пропорциональную Л' для матрицы (Л' X ) [14].

Пример 7.10. Оптимальное решение для полученной в примере 7.9 матрицы А находится следующим образом.

При нормализации А получаем матрицу:

матрица имеет вид

В этой матрице содержатся пять независимых нулей (они обведены кружками), определяющих следующее размещение с нулевой ценой:

Элемент Позиция

Нижняя граница общей протяженности соединений равна

72 (ai3 + G24 + йзз + 41 + ass) = 72 (17 + 5 + 16 + 13 -f 0) = 20,5.

При полученном размещении, как можно подсчитать, используя матрицы С и D, общая протяженность соединений равна 32 единицам.

Заметим, что полученное решение определяет перестановку с оптимальной нижней граничной оценкой, а общая длина соединений при результирующем размещении может и не быть минимальной.

Представляется интересным определить нижнюю граничную оценку общей протяженности соединений в случае, когда элементы некоторого подмножества уже размещены. Для этого можно использовать и процедуру 7.7А и процедуру 7.8А.

Процедура 7.7В

1. Вычисляем суммарную длину соединений между парами уже размещенных элементов.

2. Для каждого уже размещенного элемента i и его позиции p{i) упорядочиваем в порядке возрастания соединения Cij между i и еще не размещенным элементом / и упорядочиваем расстояния dij между р{1) и еще не занятыми позициями в порядке убывания, после чего перемножаем соответствующие элементы полученных последовательностей.

3. Располагаем в порядке возрастания длин все соединения между всеми парами элементов, которые еще не были размещены, и располагаем в порядке убывания все расстояния между незанятыми позициями, после чего поэлементно перемножаем полученные последовательности.

4. Складываем полученные на шагах 1,2 и 3 суммы. Результат определяет нижнюю граничную оценку.

Пример 7.11. Предположим, что в примере 7.8 элемент 1 был размещен в позиции 1 и элемент 4 в позиции 2. Элементы 1 и 4 имеют три соединения, а расстояние между позициями 1 и 2 равно 1. Следовательно, длина соединений между размещенными элементами равна 3.

Теперь, упорядочив элементы Ci2, Cis и Cis матрицы С и расстояния dis, di4, di5 между позициями 1 (р(1)) и 3,4,5 (неиспользованные позиции), получаем последовательности (0,2,5) и (7,4,3) соответственно. Суммируя произведения соответствующих элементов, получаем (О X 7) + (2 X 4) + (5 X 3) = 23. Повторяя эти действия для элемента 4 позиции 2, получаем (0Х6) + (0ХЗ) + (4Х2) =8.

Теперь, когда закончены вычисления для всех размещенных модулей и занятых позиций, упорядочиваем оставшиеся элементы матрицы С(с2з, 25, С35) и D (di, ds5, ds), получая соответственно (0,0,1) и (4,3,1). Поэлементное умножение дает 1. Следовательно, нижняя граница равна 3+ (23 + 8) + (1)=35.

Процедура 7.8В

1. Для каждого неразмещенного элемента i и незанятой позиции j вычисляем Uij следующим образом:

а) Для каждого элемента k, уже размещенного в позицию р{к), вычисляем Cih-djp(ii) - общую длину соединений между i и k при размещении элемента i в позиции /.

б) Располагаем содинения Cim между элементом i и любым другим неразмещенным элементом т в порядке возрастания. Располагаем расстояния c?j между / и любой другой незанятой позицией п в порядке убывания. Суммируем произведения соответствующих элементов этих двух последовательностей. Поскольку длина соединения между двумя неразмещенными элементами i и т учитывается и в Сг, р(г), и в flm, р(т)> делим полученное число на два.

в) Складываем результаты, полученные на шаге а) и шаге б),и получаем а^.

2. На основе матрицы А ищем оптимальное размещение, используя процедуру Манкреса (процедура 7.9).

3. Нижняя граничная оценка общей протяженности соединений при этом равна

2 0-1, p(i) + р,

где суммирование производится по всем номерам неразмещенных элементов, p{i) определено на шаге 2, а Lp - длина соединений между элементами, которые с самого начала уже были размещены.

Задачи физического проектирования 481 7.6.2. МЕТОД ВЕТВЕЙ И ГРАНИЦ

Задачи размещения, так же как и другие комбинаторные задачи, могут быть в принципе решены путем перебора всех возможных вариантов. При размещении М элементов на карте, содержащей Л' позиций, существует Л' возможных вариантов размещения первого элемента. Для каждого варианта размещения первого элемента существуют (Л'-1) вариантов размещения второго элемента. Процедура перебора может быть представлена деревом, содержащим Л' ярусов. На k ярусе дерева (считаем, что вершина дерева определяет нулевой ярус) k элементов уже размещены, и из каждой вершины исходят {N - k) ветвей, соответствующих (Л' - k) возможным вариантам размещения последующего элемента. Ясно, что, построив полное дерево, можно получить оптимальное решение.

Для обеспечения выбора оптимального решения в методе ветвей и границ используются нижние граничные оценки цены решения (т. е. длины соответствующих соединений). Предположим, что для различных ветвей частично построенного дерева получены нижние граничные оценки соответствующих цен. Если мы вычислим действительную цену одного возможного решения (размещения), то нет необходимости вести поиск по ветвям, исходящим из вершины, у которой нижняя граница цены превосходит цену уже полученного решения. Для дальнейшего ограничения числа рассматриваемых ветвей дерева (или определения порядка их исследования) можно использовать различные эвристические методы. К примеру, можно проверять ту ветвь, которой соответствует наименьшая нижняя граница. Таким образом, можно понизить, если не требуется найти именно оптимальное решение, вычислительную сложность процедуры. Для вычисления нижних границ в рассматриваемом методе можно использовать процедуры 7.7В или 7.8В.

Пример 7.12. Оптимальное решение задачи размещения, описываемой матрицей соединений С и матрицей расстояний D, показанными на рис. 7.22, а, может быть получено при помощи метода ветвей и границ. Исходная вершина хххх изображенного на рис. 7.22,6 дерева не занята ни одним элементом, а нижняя граница (полученная с помощью процедуры 7.7В, ее значение указано в скобках) равна 24. Вершины первого яруса Ixxx, xlxx, xxlx, xxxl соответствуют размещению элемента 1 в каждой из четырех позиций. На каждом шаге мы рассматриваем ветвь, которой сопоставлена наименьшая нижняя граница. (В случае если такая ветвь не одна, мы выбираем левостоящую. Заметим, что в зависимости от того, какой из элементов 2,3,4 будет размещен на первом ярусе, будут получены различные деревья. Представляется возможным также рассмат-

ривать на первом ярусе размещение каждого из М элементов в некоторой позиции /.) С помощью этого метода получено оптимальное решение (2, 1,3,4), которому соответствует общая протяженность соединений в 28 единиц. Вершины дерева с ценой, превосходящей или равной 28, не рассматриваются, поскольку они не приведут к решениям с меньшей ценой. Тем не менее, если мы заинтересованы в получении всех решений с минимальной ценой, надо рассматривать все ветви с ценой, равной 28.

5 L3

О 4 О J

1 3 О 2

хххх(24)

1ххх(28)

х1хх(24)

хх1х(24) XXX 1(28)

21хх(28) х12х(35)

2х1х(30) х21х(35) XX 12(28)

X 1x2(30)

2143(31)

2134(28)

Рис. 7.22. Матрицы С и D (а) и соответствующее дерево (б) перебора из

примера 7.12.

Вышеописанный метод ветвей и границ применим для задач относительно небольшой размерности. Для больших схем в общем случае остается лишь доверять субоптимальным алгоритмам размещения.

г.6.3. ИТЕРАТИВНЫЕ ПРОЦЕДУРЫ ПОИСКА СУБОПТИМАЛЬНЫХ РАЗМЕЩЕНИЙ

Большинство практических задач имеют слишком большую размерность, поэтому для того, чтобы получить их оптимальные решения, пользуются приближенными методами. Рассмотрим сначала итеративные процедуры, в которых для уменьшения цены результирующего размещения исходное размещение видо-

) Этот район Нью-Йорка имеет строгую геометрическую планировку: ряд параллельных проспектов пересекается под прямым углом рядом параллельных улиц. - Прим. перев.

изменяется путем последовательных перестановок до тех пор, пока не будет получено локально-оптимальное решение. Так же как и в задаче разбиения, исходное размещение может быть выбрано произвольно или на основе некоторого конструктивного метода. Несколько таких конструктивных методов рассматриваются в следующем разделе.

Чтобы ограничить сложность вычислений, для перестановки

выбирают обычно пару элементов. Из возможных вариантов выбора отбирают локально-оптимальный. Было предложено простое правило выбора: выбирать элемент с наибольшим потенциальным вкладом (определяемым как общая длина его соединений при текущем размещении минус нижняя граничная оценка протяженности этих соединений). Далее определяется соответствующее улучшение при перестановке местами этого элемента с каждым из Л'- 1 оставшихся и осуществляется локально-оптимальный обмен. (В алгоритме разбиения Керниха-на -Лина эти действия соответствуют выбору элемента с максимальным значением D в качестве одного из пары обмениваемых между собой элементов.) Эта процедура может повторяться для различных пар элементов до тех пор, пока возможно дальнейшее уменьшение цены.

В обсуждаемых алгоритмах размещения до сих пор предполагалась известной матрица расстояния. Соединения между элементами часто осуществляются вертикальными и горизонтальными отрезками. В такой геометрии (часто называемой манхэттенской геометрией) ) расстояние между двумя точками с координатами (Xi, г/i) и (Хг, г/г) определяется как xi -X2I + + 11 - №|. где х| обозначает абсолютную величину х. Оно называется прямолинейным расстоянием между двумя точками. В следующем примере мы получим субоптимальное размещение для этого определения расстояния.

Пример 7.13. Рассмотрим схему, изображенную на рис. 7.23, а, при исходном разбиении, соответствующем рис. 7.23, б. Мы предполагаем, что элементы должны быть размещены в показанной сетке. В качестве приближенной оценки прямолинейного расстояния будем использовать число пересечений с линиями сетки. Общая протяженность соединений при исходном размещении, показанном на рис. 7.23, б, равна 20.

У элемента 5 общая длина соединений равна 18, а нижняя граница общей длины связанных с ним соединений (при длине каждого соединения с k зажимами, равной /г-f-1) равна 11.

+1 -2 -2

4 +2

Поскольку наименьшая цена достигается при перестановке местами элементов 5 и 4, мы меняем местами эти элементы; ре-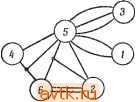

Рис. 7.23. Схема (а) из примера 7.13 и ее исходное размещение (б).

зультирующий план размещения показан на рис. 7.24, а. Соответствующая цена равна 16.

Не считая элемента 5, у элемента 4 теперь наибольший потенциальный вклад. Изменение цены при обмене между элементом 4 и i при =1,2,3,5,6 иллюстрируется следующей таблицей:

1 2 3 5 6

-1 +2 +1 +4 О

Потенциальный вклад равен 7, что больше вкладов других элементов, и, следовательно, в обмене должен участвовать элемент 5. Изменение цены при обмене элементов 5 и i при i - = 1,2,3,4,6 иллюстрируется следующей таблицей:

1 2 3 4 6