графа путем представления всех элементов петли обратной связи одним элементом графа, имеющим вес w, где w - число элементов в петле обратной связи. Если w <. М, некоторого макси--мального числа элементов в одном модуле, то для таких схем можно использовать методы разбиения ациклических графов.

Как указывалось выще, число вариантов разбиения N-эле-ментной схемы на модули, содержащие не более М элементов, превышает N\/{K\ {М\)), где k = [N/M]. Можно показать, что для минимизации максимальной задержки в схеме необходимо рассматривать только такие размещения пучков, при которых соседние вершины (т. е. логические элементы, непосредственно соединенные друг с другом) принадлежат одному пучку. Однако число таких размещений при больших N недопустимо велико, и для решения общей задачи необходимо использовать процедуры поиска субоптимальных решений. Эффективное получение оптимальных решений возможно только в отдельных специальных случаях.

7.5.1. ОПТИМАЛЬНОЕ РАЗБИЕНИЕ ДРЕВОВИДНЫХ ГРАФОВ

Рассмотрим граф, все вершины которого имеют единичный коэффициент разветвления по выходу. Такой граф назьшается сходящимся деревом. Предшественниками вершины t, обозначаемыми через P(i), являются все вершины, соединенные непосредственно или косвенно со входом вершины i. Весом Wi вершины i назовем число элементов исходной схемы, представленных этой вершиной. Предположим, что общий вес всех вершин одной карты не должен превышать М, и сначала не будем учитывать ограничения на число выводов. Будем присваивать числовые метки вершинам графа таким образом, чтобы все вершины, имеющие одинаковые метки, определяли пучок, а наибольшая метка оказалась бы равной длительности задержки при полученном разбиении.

Для сходящихся деревьев может быть предложена следующая процедура расстановки меток, обеспечивающая минимизацию наибольшего значения метки и, следовательно, минимизацию длительности задержки схемы, веса вершин которой не Превышают М.

Процедура 7.5 (разбиение сходящегося дерева, минимизирующее длительность задержки)

1. Присвоить метку О вершинам, представляющим входы схемы.

2. Вершине t, все предшественники которой уже имеют метки, присвоить метку k; k - наибольшая метка, назначенная предшественникам i, если Wi-{-E.Wj М, где сумма берется по всем вершинам /, являющимся предшественниками i и имею-

щим метку k; в противном случае присвоить вершине i метку

3. Множество связанных между собой вершин с одинаковыми метками определяет пучок, а несвязанные между собой вершины, имеющие одинаковые метки, можно сгруппировать в один пучок при условии, что вес каждого такого пучка не превышает М. Для результирующего разбиения справедливо условие, что для всех вершин пучка Zj М. Длительность задержки, определяемая этим разбиением, равна наибольшей числовой метке.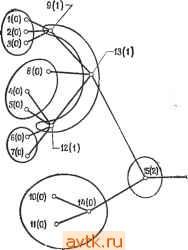

Рис. 7.16 Разбиение

с минимальной длительностью задержки для сходящегося дерева.

Заметим, что, вообще говоря, могут существовать разбиения, имеющие такую же длительность задержки, но с меньшим числом пучков, в этом смысле описанная процедура не оптимальна. Тем не менее не существует разбиения на пучки, удовлетворяющие ограничению по весу, обеспечивающего меньшую длительность задержки (предлагается доказать самостоятельно).

Пример 7.5. Рисунок 7.16 иллюстрирует применение описанной процедуры. Полагаем М = 3 и tw = 1 для всех /. Присвоенные вершинам числовые метки указаны в скобках. Соединенные между собой вершины с одинаковыми метками образуют пучок, не соединенные между собой вершины с одинаковыми метками могут быть сгруппированы в пучок для уменьшения числа пучков (но не длительности задержки) при выполнении ограничений по весу. Легко проверить, что длительность задержки при результирующем разбиении равна 2.

Рассмотрим теперь графы, вершины которых имеют единичный коэффициент разветвления по входу. Такие графы называются расходящимися деревьями. Процедуру 7.5 можно модифицировать для построения разбиений расходящихся деревьев, обеспечивающих минимальную длительность задержки, изменив правило присвоения меток.

Процедура 7.5А (разбиение расходящегося дерева, минимизирующее длительность задержки)

1. Присвоить всем выходным вершинам метку 0.

2. Вершине i все предшественники которой уже имеют метки, присвоить метку k; к - наибольшая из меток предшественников i, если Wi + 2]tг>/И (где сумма берется по всем вершинам /, являющимся предшественниками вершины i и имеющим метку к); в противном случае вершине i присвоить метку

3. Образовать пучки, состоящие из связанных между собой вершин, имеющих одинаковые метки. Не соединенные между собой вершины с одинаковыми метками также могут быть сгруппированы вместе.

Задача разбиения при минимизации длительности задержки усложняется в случае ациклических графов, не являющихся ни сходящимися, ни расходящимися деревьями. На рис. 7.17, а показан такой граф, а на рис. 17, б и е отражены результаты попыток использовать для разбиения графа соответственно процедуры 7.5 и 7.5А при Wi - 1 для всех вершин и М = 3. Заметим, что изображенный на рис. 7.17,6 пучок вершин, имеющих метку 3, содержит четыре вершины и, таким образом, ограничение М = 3 нарушено. На рис. 7.17, е также есть пучок из четырех вершин, имеющих метку 2. Следовательно, описанные процедуры нельзя применять для графов, не являющихся сходящимися или расходящимися деревьями.

Для любого ациклического графа существует, однако, возможность получения решений, обеспечивающих минимальную длительность задержки на основе дублирования вершин. Дублирование вершины графа соответствует введению в схему дубликатов соответствующего логического элемента (или элементов) с теми же самыми входами. Например, если ввести А' - дубликат вершины А изображенного на рис. 7.17,6 графа, то мы получим граф, изображенный на рис. 7.18. Обращаясь к рис. 7.17,6, мы видим, что вершина А входит в пучок из четырех вершин. Если мы определим пучок как множество вершин с одинаковыми метками, таких, что ни один из предшественников этих вершин не имеет такой же метки, то окажется, что вершина А входит в два пучка С\ = (Л, В, С), Сг = (Л, С, D) и при этом С\ S Сг, Сч S С\. Два пучка, обладающие указанным свой-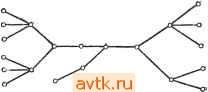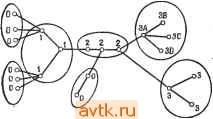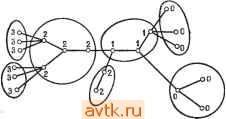

Рис. 7.17. Разбиение графа (а) на основе процедуры 7.5(6) и процедуры

7.5А (в).

ством, называются несовместимыми. Именно наличие несовместимых пучков обусловливает сложность применения процедуры 7.5 к ациклическим графам общего вида. (Заметим, что использование процедуры 7.5 для сходящихся деревьев не приводит к образованию несовместимых пучков.) Мы выяснили, что для преодоления этой сложности следует прибегнуть к дублированию. Таким образом, в том случае, когда допускается дублирование, можно воспользоваться следующей процедурой разбиения ациклического графа, обеспечивающей минимальную длительность задержки. Процедура 7.6

1. Вершинам присваиваются метки в соответствии с алгоритмом разбиения сходящихся деревьев (процедура 7.5).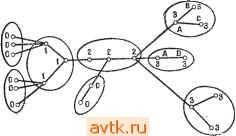

Рис. 7.18. Разбиение с минимальной д.чите.чьностью задержки при испо.чьзо-

вании дублирования.

копии /р вершины / в графе G образуется дуга {im,jn), где т~ п, если i и / имеют одинаковые метки в графе G, и т выбирается произвольно, если i и / имеют разные метки в графе G.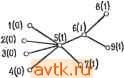

Рис. 7.19. Разметка графа в соответствии с процедурой 7.5 (а) и разбиение с минимальной длительностью задер)!ски при использовании дублирования (б).

Пример 7.6. Для изображенного на рис. 7.19, а графа, представляющего схему с направлением распространения сигналов слева направо, положим М - 3 и Wi= I для всех вершин. В скобках указаны метки, полученные при использовании процедуры 7.5. Заметим, что вершина 5 входит в три несовместимых пучка {5,7}, {5,6,8}, {5,6,9}, два из которых содержат вершину 6. Полученный граф G изображен на рис. 7.19,6. Результирующее разбиение соответствует единичной длительности задержки.

2. На основе исходного графа G строится новый граф G следующим образом.

Через Cj обозначается число несовместимых пучков графа G, содержащих вершину /. Тогда G содержит Cj копий вершины h il hy 4. h.- Д- каждой дуги (t,/) графа G и каждой

Вообще говоря, можно уменьшить требуемое в процедуре 7.6 число дублированных вершин, однако в настоящее время неизвестны алгоритмы, обеспечивающие минимум длительности задержки при минимальном числе дублированных вершин. В случае если дублирование не допускается, минимальная длительность задержки возрастает. На рис. 7.18 изображена полученная при использовании дублирования реализация с минимальной длительностью задержки для графа, показанного на рис. 7.17, а. Без дублирования минимальная длительность задержки оказывается равной 5. (Упражнение.) В общем случае задача получения решений с минимальной длительностью задержки для ациклических графов без использования дублирования оказывается существенно более сложной, хотя соответствующая процедура действительно существует для ациклических графов, в которых для любой пары вершин i, j существует единственный путь из i в / [21].

7.5.2. РАЗБИЕНИЯ, ОБЕСПЕЧИВАЮЩИЕ

МИНИМАЛЬНУЮ ДЛИТЕЛЬНОСТЬ ЗАДЕРЖКИ ПРИ УЧЕТЕ ОГРАНИЧЕНИЙ НА ЧИСЛО ВЫВОДОВ

Для древовидных графов представляется возможным обобщить процедуру, описанную в предыдущем разделе, при учете ограничений на число выводов. Обозначим через р{С) число выводов, необходимых для пучка С, а через R {i, k) - число имеющих метку k вершин, являющихся предшественниками вершины L В сходящемся (расходящемся) дереве для двух пучков Ci и Сг, таких, что Сх Сг, и вершин, принадлежащих Сг, не принадлежащих Сх и являющихся последователями (предшественниками) (непосредственными или косвенными) вершин из Сх, справедливо, что р(Сх) piCz). В силу этого условия монотонности процедура 7.5 (и 7.5А) может быть модифицирована для построения разбиений, в которых каждому пучку требуется не более Р выходов.

Процедура 7.5В

1. Присваиваем метку О всем входным'вершинам.

2. Пусть i - вершина без метки, все предшественники которой имеют метки, и пусть k - наибольшая метка, присвоенная предшественникам i. Тогда присваиваем метку k вершине i, если

а) Wi + X! г / < М,

б) рша, k)[j{i}xp.

Если любое из этих условий нарушено, то присваиваем вершине t метку А + 1.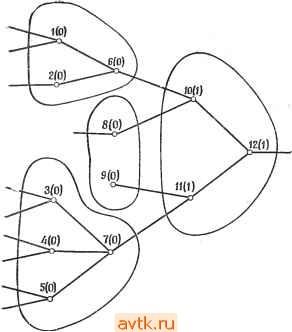

3adep>HKcf={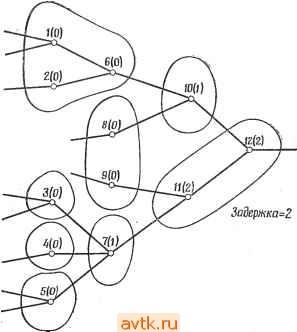

Рис. 7.20. Разбиение графа при различных ограничениях на число выводов.

ы

ta S

е-

о

о о в

Пример 7.7. На рис. 7.20, а показано разбиение обеспечивающее минимальную длительность задержки при М = 4 без ограничения на число выводов; разбиение той же схемы при М - А и ограничении на число выводов (Р=4) показано на рис. 7.20, б.

Для графов, представляющих схемы более общего вида, условие монотонности, вообще говоря, не выполняется. Разбиение таких схем при ограничении на число выводов существенно усложняется. Более сложной является задача построения разбиения, минимизирующего длительность задержки, для схем с многооконечными соединениями.

7.6. ЗАДАЧА РАЗМЕЩЕНИЯ

После разбиения схемы возникает задача размещения отдельных ее подсхем и элементов в подсхемах. При этом говорят о так называемой задаче размещения.

В зависимости от используемой технологии задача размещения возникает на различных этапах физического проектирования. При н^спользуемой в настоящее время технологии производства интегральных схем задача размещения решается на трех различных уровнях. Во-первых, отдельные элементы должны быть размещены на кристаллах или включены в модули. После этого ИС должны быть размещены на картах или платах и соединены между собой. И наконец, карты должны быть размещены на несущей плате или каркасе и соединены между собой. При дискретной технологии отдельные компоненты размещаются на платах, которые в свою очередь размещаются на каркасе. Решение задачи размещения, которое будет нами рассматриваться, может быть использовано на любом из перечисленных этапов; при этом в зависимости от этапа существенными оказываются различные параметры оптимизации.

Мы будем говорить о размещении элементов на плате. Это соответствует размещению множества из М элементов по Л' М позициям платы. Можно рассмотреть целый класс задач поиска размещений, оптимизирующих некоторый параметр. Конечной же целью является упрощение последующей задачи определения путей соединений между элементами карты. Эти соединения должны соответствовать многим электрическим и топологическим ограничениям. При этом нельзя указать критерий, одновременно удовлетворяющий всем этим (возможно, противоречивым) ограничениям. Наиболее часто используемым критерием качества размещения модулей является минимизация общей длины соединений между элементами. Обычно этот компромиссный критерий соответствует, хотя бы отчасти, большинству реальных требований. Оптимизация по этому критерию позволяет упростить монтаж схемы и, следовательно, уменьшить расходы, связанные с ее производством.

Рис. 7.21. Схема (а), соответствующий ей граф (б) и оптимальное размещение (е) для схемы и для графа (г).

Представление в виде графов схем с многооконечными сетями, как и в случае задачи разбиения, сталкивается с определенными сложностями. Если мы представим такую схему в виде биграфа, то множество вершин, соответствующих сигнальным сетям, нельзя разместить однозначно при размещении остающихся вершин, соответствующих .элементам схемы. Если мы представим такую схему парным графом, каждая вершина которого соответствует элементу схемы, а дуга между вершинами I и / соответствует сигнальной сети, содержащей элементы i и /, то оптимальное размещение для этого графа может не соответствовать оптимальному размещению для реальной схемы.

Рассмотрим изображенный на рис. 7.21,6 первый граф, соответствующий схеме рис. 7.21, а. Пусть модули надо разместить в линейном порядке так, чтобы минимизировать длину соединений в предположении, что расстояние между соседними пози-

циями равно I. Можно показать, что приведенное на рис.7.21,е размещение является оптимальным и соответствует общей длине соединений в 8 единиц. При таком размещении общая длина всех соединений для графа, изображенного на рис. 7.21,6, равна 24 единицам. Однако общая длина соединений показанного на рис. 7.21, г размещения равна 22, при этом общая длина соединений, необходимых в соответствии с рис. 7.21, а, равна 9.

Задача размещения для схем, содержащих сети только с двумя зажимами, может быть сформулирована следующим образом: на плате, имеющей N М позиций при заданной матрице расстояний D = {dij], где йц - расстояние между позициями i и у, и матрице смежности С = [c,j], где Cjj - число соединений между модулями i и у, разместить М элементов таким образом, чтобы минимизировать Z] c.dp.jpjj, где p{i)-позиция, занимаемая модулем i, а суммирование производится по всем г, /, i < /. Если Л' > М, мы расширяем С, добавляя ;V - М столбцов и строк, представляющих фиктивные, не имеющие соединений элементы. Заметим, что матрицы С я D симметричные с нулевыми диагональными элементами.

Число возможных размещений М элементов по Л' позициям

равно 1 д| \N ) число сочетаний из Л' эле-

ментов по М. Число рассматриваемых вариантов уменьшится в два раза, если мы учтем, что перестановки {\,2,...,Щ и {N, N - 1,..., 2, 1) эквивалентны с точки зрения длины соединений (чтобы убедиться в этом, достаточно изменить ориентацию карты). Однако при больших Л' необходимо снова обратиться к процедурам поиска субоптимальных решений. Многие из известных в настоящее время процедур пригодны лишь для схем, имеющих только двухоконечиые сети. Задача существенно осложняется для схем с многооконечными сетями, поскольку при > 2 существует много вариантов взаимного соединения k точек равного потенциала. Такая задача будет рассмотрена в конце этой главы в рамках решения задачи трассировки. (Метод соединения может влиять на оптимальность размещения.) Мы рассмотрим некоторые процедуры, разработанные для графических моделей, поскольку они могут быгь полезными в более общих случаях.

7.6.1. НИЖНЯЯ ГРАНИЧНАЯ ОЦЕНКА

МИНИМАЛЬНОЙ ДЛИНЫ СОЕДИНЕНИЙ

Иногда требуется получить граничную оценку решения. Очень грубую нижнюю граничную оценку решения можно полунить весьма просто.